СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза: бурильные машины для тоннеля под Ла-Маншем
Сооружение тоннеля под Ла-Маншем между Францией и Великобританией началось в декабре 1987 г. Проходка осуществлялась с двух сторон, и первая стыковка тоннелей состоялась в ноябре 1990 г. Тоннель имеет протяженность 37,8 км и проходит на глубине 60 м ниже уровня моря. Его строительство обошлось в 14 млрд. долларов и было завершено в 1992 г. Тоннель позволяет ежедневно пропускать 50 поездов. Он является кратчайшим путем между Европой и Великобританией, а поездка из Лондона в Париж занимает всего 3 часа.
Во время проходки тоннеля машины с двух сторон двигались навстречу друг другу. Чтобы соединиться в середине Ла-Манша с заданной точностью, направление движения машин задавалось прецизионной лазерной системой. На рис. 4.21 изображена структурная схема системы управления бурильной машиной, где У(х) соответствует действительному угловому направлению движения машины, a R(s) — заданному углу. Влияние нагрузки на машину представлено возмущением D(s).
|
D(s) |
|
E(s) |
|
К + 11s |
|
- Y(S) Угол |
|
Рис. 4.21 Структурная схема системы управления бурильной машиной |
|
R(s) - ІО Желаемый — угол |
|
Бурильная машина СЦз) |
|
s(s + 1) |
Цель синтеза состоит в выборе такого значения коэффициента К, при котором реакция системы на входное воздействие, соответствующее заданному значению угла, имела бы желаемый вид и при этом ошибка, вызванная возмущением, была минимальной. По формуле Мейсона выходную переменную с учетом двух входных сигналов можно представить в виде:
Y (s) = T(s)R(s) + Td (s)D(s) = ,K+lh R(s) + —------------------ 1 D(s).---------- (4.59)
.r+12s + A: s2+2s + K
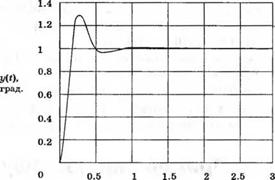
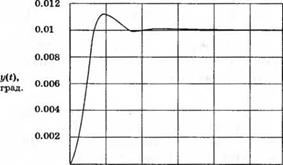
Чтобы уменьшить влияние возмущения, коэффициент К желательно иметь больше 10. Если выбрать К = 100 и положить d(t) = 0, то переходная характеристика системы при единичном ступенчатом воздействии r(t) будет иметь вид, представленный на рис. 4.22(a). Если же положить r(t) = 0 и считать, что возмущение имеет вид единичной ступеньки, то реакция системы примет форму, представленную на рис. 4.22(6). Мы видим, что влияние возмущения очень незначительно. При К = 20 реакции системы на еди-
|
Время (с) |
Рис. 4.22 а)
Реакции y{f) на
(а) единичную ступеньку r[t) и
(б) на единичную ступеньку
ct) при К = 100
б)
|
0 0.5 1 1.5 2 2.5 3 Время (с) |
|
|
|
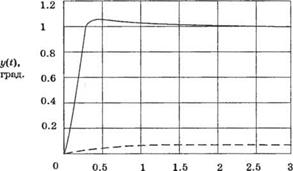
Рис. 4.23 Реакции y{f) на единичную ступеньку rt) (сплошная кривая) и на единичную ступеньку d{t) (пунктирная кривая) при К = 20 |
Время, (с)
ничные ступенчатые воздействия/ (/) и d(t) изображены на рис. 4.23. Поскольку перерегулирование на переходной характеристике небольшое (менее 4%), а установившееся значение достигается за 2 секунды, можно остановиться на величине К = 20. Результаты сведены в табл. 4.1.
Установившаяся ошибка системы при единичном ступенчатом воздействии /-(/), т. е. при R(s) = І/s, равна
lim e(t) = lim s------ - J-—— -- = 0. (4.60)
t-> со s->0 К + 1 Is s
1 +-------
s(s + 1)
Установившееся значение y(t) при единичном ступенчатом воздействии d(t), т. е. при £>(■') = І/s, и в случае /•(/) = 0 равно
і і
(4.61)
lim y(t)= lim ------------------- = —
i-*» .v->oj(j-i-12)+A: К
Это значение при К = 100 и 20 составляет соответственно 0,01 и 0,05.
В заключение найдем чувствительность системы к изменению передаточной функции объекта G(s). Используя выражение (4.12), имеем:
Ч> • " («2) s(s+12) + K
|
S ~К |
На низких частотах (|s| < 1) чувствительность приближенно равна
(4.63)
Мы видим, что чувствительность обратно пропорциональна значению К. Поэтому в данном случае можно считать, что выбор К =20 является приемлемым компромиссом при синтезе системы.
|
Таблица 4.1. Реакции системы управления бурильной машиной при разных значениях К
|