Влияние ограниченности размеров тела на процессы распространения теплоты
До сих пор рассматривались процессы распространения теплоты в неограниченных телах. Это упрощало расчеты, так как не нужно было вводить граничные условия.
Несмотря на то что свариваемые изделия всегда имеют ограниченные размеры, в большинстве случаев для оценки температурного поля и определения термических циклов нет необходимости учитывать влияние границ тела. Однако в ряде случаев такой учет оказывается необходимым вследствие значительного влияния отраженной от границ тела теплоты на температурное поле. Границы тела в первом приближении можно считать не пропускающими теплоты, т. е. считать адиабатическими (см. п. 5.2).
В п. 5.2 указывался прием, с помощью которого можно удовлетворить адиабатическому условию и получить действительное распределение температур, зная закон распределения температуры в неограниченном теле. Этот прием используется также и для описания перемещающихся температурных полей.
ДВИЖЕНИЕ ИСТОЧНИКА ВБЛИЗИ КРАЯ ТЕЛА
|
|
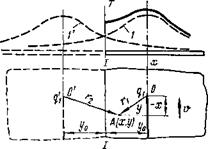
Допустим, что источник теплоты перемещается на некотором расстоянии от края пластины г/о (рис. 6.15). Считая границу /—/ адиабатической, создадим отражение теплоты от нее. Этого можно достигнуть, если предположить, что пластина бесконечна и в ней движутся одновременно с одинаковой скоростью два источника одинаковой мощности. Расстояние между действительным и фиктивным источниками равно 2у0. Распределение температуры в некотором произвольном сечении от действительного qi и фиктивного q источников теплоты в бесконечной пластине показано Рис - 6Л5- Схема ввеДения дополни-
иг» с і г тельного движущегося источника д
рис. O. I5 штриховыми ЛИ - для учета отражения теплоты от грани-
ниями 1 и V соответственно. цы / —/
Распределение температуры с учетом отражения теплоты от границы /—/ представляет собой сумму температур от действительного и фиктивного источников теплоты и показано на рисунке сплошной линией.
Приращение температуры в некоторой точке А определяется согласно уравнению (6.26) следующей формулой:
=w'-ni *.(г, лЛ^+4-) +
+ M/*V-ST+4)] ■ (6.48)
где _____________
г, = - у/х2 + і/2; г2 = л/х2 + (2уа—у)2 •
Аналогично может быть определено приращение температуры и в случае, если источник теплоты движется под некоторым углом к границе тела. С помощью таких же искусственных приемов определяется температура при движении точечного источника теплоты вблизи края массивного тела.
НАГРЕВ ДВУХ УЗКИХ ПЛАСТИН
|
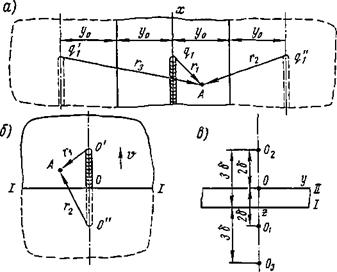
Рис. 6.16. Схемы введения дополнительных источников для учета отражения теплоты от границ тела: |
|
о — при сварке узких пластин; б — при сварке от края тела; в — прн движении точечного источника по поверхности плоского слоя |
При нагреве двух узких пластин, каждая из которых имеет ширину I/O, отражение теплоты приближенно можно учесть, вводя два дополнительных фиктивных источника q—q" — t71
(рис. 6.16, а). Температура точки А должна определяться как сумма температур от трех источников, действующих в бесконечной пластине. Для весьма узких пластин необходимо вводить многократное отражение теплоты от границы аналогично тому, как это сделано в случае нагрева точечным источником теплоты, движущимся по поверхности пластины (см. ниже).
НАГРЕВ ОТ КРАЯ ТЕЛА
Весьма распространенный случай — нагрев пластины, когда источник теплоты начинает свое движение от ее края (рис. 6.16,6). Помимо того что здесь происходит процесс теплонасыщения, наблюдается также отражение теплоты от границы /—/. Учет отражения, если это необходимо, может быть выполнен путем введения фиктивного источника теплоты, который начинает движение одновременно с действительным источником теплоты из точки О, перемещаясь в противоположном направлении. Оба источника теплоты действуют в бесконечной пластине. Приращение температуры в точке А определится как сумма приращений температур от действительного и фиктивного источников теплоты.
ТОЧЕЧНЫЙ ИСТОЧНИК НА ПОВЕРХНОСТИ ПЛАСТИНЫ
Этот случай близок к наплавке валика на пластину. В зависимости от толщины расчет температуры ведут по одной из трех схем. Если пластина тонкая, то предполагают, что источник выделяет теплоту равномерно по толщине листа и расчет проводят, как для линейного источника теплоты в пластине. В толстых плитах отражением теплоты от нижней границы пренебрегают и расчет ведут по схеме точечного источника теплоты на поверхности полубесконечного тела. Наконец, если пластина не удовлетворяет первым двум схемам, то выбирают схему плоского слоя с точечным источником теплоты на поверхности (рис. 6.16, в), принимая, что обе поверхности не пропускают теплоту.
При расчете температур в процессе сварки нельзя однозначно отнести пластину к тонкой или толстой. Если тепловыделение от источника теплоты происходит почти по всей толщине пластины, то она может быть отнесена к тонким, если даже ее толщина измеряется многими миллиметрами. Напротив, пластина толщиной 1 мм должна быть отнесена к толстым, если на ее поверхности действует весьма концентрированный маломощный Источник теплоты, не вызывающий глубокого проплавления, например остросфокусированный лазерный луч.
Действительный точечный источник теплоты принимают перемещающимся по поверхности полубесконечного тела. Для учета отражения теплоты источника О от границы / вводят фиктивный точечный источник теплоты 0 на поверхности полубесконечного тела (на расстоянии 26 от границы //). В свою оче-
|
а) т
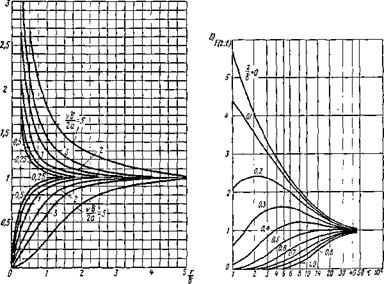
Рис. 6.17. Номограммы для определения т и F (г, t) |
редь, теплота фиктивного источника Oi будет отражаться от плоскости //, что должно быть учтено расчетной схемой. С этой целью вводят фиктивный источник О2 на расстоянии 26 от плоскости II. Однако теплота источника 02 будет отражаться от границы I, что требует введения фиктивного источника О3. Этот процесс может быть продолжен до бесконечности. Суммирование приращений температурных полей от всех точечных источников мощностью q, перемещающихся со скоростью v в предельном состоянии, дает уравнение
П= +оо оо
АТ -2?_______ vx/(2a)__ у . d-v2t/{Aa)-Hl/{Aat). (6 49)
А' - ср(4яа)3/2 n}_J0 t™ ' '
Rl =JC2 2 -К 2 —2«б)2, (6-50)
где п — целые числа от — оо до + оо.
Численное определение приращений температуры проводят по формуле
<65|>
при помощи номограммы для определения коэффициента т, соответствующего верхней и нижней плоскостям плоского слоя (рис. 6.17, а) и выражающего отношение приращений температуры на поверхности плоского слоя, нагреваемого точечным
источником, к приращению температуры пластины, вызываемой линейным источником. Для z = 0 т>1, для г = б т < 1.
|
|
|
|
|
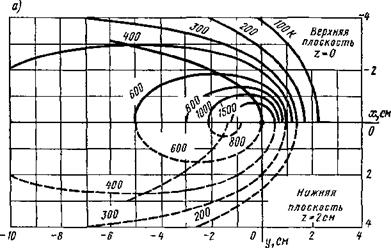
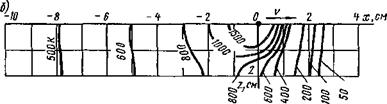
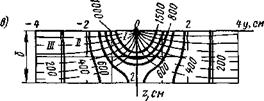
Рис. 6.18. Температурное поле предельного состояния при наплавке иа лист толщиной 2 см (^= 4000 Вт, у = 0,1 см/с, Я = 0,4 Вт/(см*К), а = 0,1 см2/с): а — изотермы и кривые максимальных приращений температур иа верхней (z = 0) и нижией (г = 6) плоскостях пластины; 6 — изотермы и кривые максимальных приращений температур о продольной плоскости xOz в — изотермы и нормальные к ним линии теплового потока в поперечной плоскости yOz |
Характер температурного поля в плоском слое (рис. 6.18) в общем случае позволяет выделить три зоны. В зоне /, прилегающей к источнику теплоты, распределение температуры мало отличается от распределения в полубесконечном теле. В зоне ///, находящейся от источника теплоты обычно на расстоянии, равном нескольким толщинам пластины, температура по толщине
пластины выравнена и температурное поле приближается к полю линейного источника теплоты в пластине. Зона //—переходная. Соотношение между размерами трех зон может изменяться в зависимости от режима сварки и свойств материала.
Пример 8. На стальной лист толщиной 18 мм наплавляют валик, мощность источника q = 4000 Вт, скорость его перемещения v = 3,6 м/ч = 0,1 см/с, теплофизические коэффициенты Л= 0,04 Вт/(см-К), а = 0.09 см2/с. Рассчитать приращение температуры предельного состояния в точках Л и В, находящихся на верхней и на нижней плоскостях на расстоянии 20 мм позади источника теплоты по оси его движения.
Координаты точки А: х = — 2 см, j/=0, 2 = 0, г = 2 см; точки В: х = = — 2 см, у — 0, 2 = 2 см, г = 2 см. Используем формулу (6.50).
Для определения коэффициента m вычисляем значения критериев:
v6 _ 0.М.8 г _ 2 _
2а ~ 2-0,09 ’ 6 1,8 ’ '
Для точки А значение m находим при 2 = 0 по кривой о5/(2а) = 1 в верхней части номограммы рис. 6.17, а: тА = 1,1. Для точки В значение т находим при 2 = 8 по кривой о6/(2а) = 1 в иижней части номограммы: тв = 0,9.
Приращение температуры предельного состояния определяем по схеме пластины с равномерным по толщине выделением теплоты, т. е. по формуле (6.23) при х = — 2 см, г = 2 см. Это значение входит как сомножитель т во вторую часть формулы (6.51):
Д7- = _4_ = 885е1-"/С0 (1,11) = 885-3,034-0,36 = 967 К.
2яАо ' 2а г
Приращение температуры точки А верхней плоскости
ДГд = тААТ = 1,1-967 = 1073 К.
Приращение температуры точки В нижней плоскости
АТВ = твАТ = 0,9-967 = 870 К.
На расстоянии 2 см позади источника теплоты разность температур по толщине листа составляет 1073 — 870= 203 К.
БЫСТРОДВИЖУЩИЙСЯ ТОЧЕЧНЫЙ источник НА ПОВЕРХНОСТИ ПЛАСТИНЫ
В предыдущем случае предполагалось, что точечный источник теплоты может перемещаться по поверхности пластины с произвольной, в том числе и с малой, скоростью. При больших скоростях перемещения точечного источника теплоты, как это показано в п. 6.4, можно не принимать во внимание процесс распространения теплоты вдоль оси движения источника, а рассматривать только распространение теплоты вдоль осей Оу и Oz. Таким образом, процесс распространения теплоты в рассматриваемом случае представляется как распространение теплоты от мгновенного источника, выделившего теплоту в точке О в момент времени t — 0 (см., рис. 6.16, в);
п — bt
A7’ = -£rF(2,0---rr-, ■ (6-52)
t>oCp sj 4лat
где функция F(z, t) выражает процесс распространения теплоты вдоль оси Oz с учетом отражения его от плоскости / и может быть представлена двояко: либо как сумма полей приращений температур множества мгновенных источников теплоты (см. рис. 6.16, в)
+оо
F [Z, t) =£ _2£=е-( V( 4^) (653)
—оо v4nat
(л=0,1;—1,2;—2;...; -|-оо;—оо),
либо с использованием ряда Фурье
со
F{z, t) = 1 +22 cos kn(z/b) e~kVat^2. (6.54)
к— 1
Для облегчения расчетов на рис. 6.17,6 представлена номограмма для определения численных значений F(z, t) в зависимости от z/б и безразмерного времени % = at/б2. При т > >0,5 F (z, t) « 1.
В формуле (6.52) Ь = 2а/(срб), в формулах (6.52), (6.53) и
(6.54) t — время, прошедшее с момента пересечения источником теплоты плоскости, где находится рассматриваемая точка.
Используя рассмотренные выше принципы учета ограниченности размеров тела, можно определять температуру и в телах других форм.