ТЕОРИЯ сварочных процессов

Периоды теплонасыщения и выравнивания температур при нагреве движущимися источниками теплоты

ПЕРИОД ТЕПЛОНАдыЩЕНИЯ

В п. 6.2 были рассмотрены три основных случая нагрева тел движущимися источниками теплоты — точечным, линейным и плоским. Там же были приведены формулы для определения температур в случае неустаиовившегося температурного поля.

Интегралы в уравнениях (6.21), (6.25) и (6.29) неберущие - ся, поэтому приращение температур в стадии теплонасыщения удобнее вычислять по номограммам.

Представим приращения температуры АТ в периоде теплона­сыщения как произведение приращения температуры в предель­ном состоянии ЛТ'пр на коэффициент теплонасыщения ф:

АТ = фАГпр. (6.32)

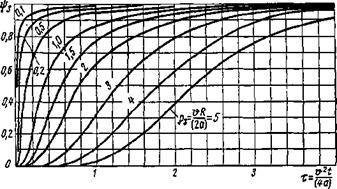
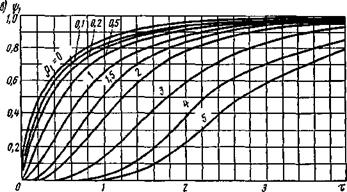
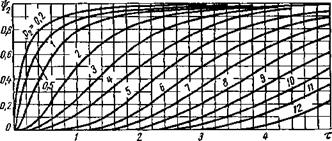
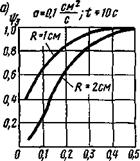
Коэффициент теплонасыщения для трех основных схем нагре­ва при сварке определяют по номограммам, приведенным на рис. 6.11, в зависимости от безразмерных критериев времени т и безразмерных расстояний от источника теплоты до рассматри­ваемой точки р.

Номограмма для определения ф3 (рис. 6.11, а) в случае то­чечного источника теплоты построена в зависимости от крите­риев

Рз = vR/(2a); т3 = v2tH/(4a), (6.33)

номограмма для определения фг (рис. 6.11,6) в случае линей­ного источника теплоты построена в зависимости от

Р’=ІГ/і+ч£: — тМ'+Чг)- <“4>

номограмма для определения ф] (рис. 6.11, в) в случае плоского источника теплоты построена в зависимости от

P1=^V,+J^; „=.£(,+ «•■.). ,6.35)

Предельное приращение температур АТп? в движущейся ко­ординатной системе, начало которой совпадает с источником теплоты, вычисляют по формулам (6.22), (6.26), (6.30). Из рассмотрения характера кривых на номограммах (см. рис. 6.11) следует, что чем ближе расположена к источнику теплоты рас­сматриваемая точка тела, тем раньше и тем быстрее возрастает

а — фз для точечного источника н полубесконечиом теле; б — фг для линей­ного источника в бесконечной пластине; в — ф[ — для плоского источника в бесконечном стержне

температура в ней. В зоне, расположенной ближе к источнику теплоты, период теплонасыщения заканчивается раньше, чем в удаленных зонах.

На продолжительность периода теплонасыщения существен­но влияет скорость движения источника теплоты V. Чем быстрее движется источник, тем больше коэффициент теплонасыщения (рис. 6.12, а).

Чем более стеснен поток теплоты, тем медленнее идет про­цесс тепло насыщения. Поэтому при прочих равных условиях про­цесс теплонасыщения в стержне заканчивается позже, чем в пластине, а в пластине — позже, чем в массивном теле.

ПЕРИОД ВЫРАВНИВАНИЯ ТЕМПЕРАТУРЫ

После прекращения действия источника теплоты наступает период выравнивания температур. Теплота, введенная ранее, продолжает распространяться в теле и уходить в окружающую среду.

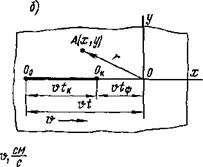
Температуру в период выравнивания можно определять пу­тем использования фиктивного источника теплоты и стока теп­лоты аналогично случаю, рассмотренному выше (в п. 6.1). Рас­смотрим случай, когда источник теплоты в точке Ок прекратил движение и перестал действовать (рис. 6.12,6). Будем, однако, предполагать, что фиктивный источник теплоты той же мощно­сти продолжает свое движение с той же скоростью V. Вместе с ним движется фиктивный сток теплоты такой же мощности, как источник. Очевидно, что источник и сток теплоты будут взаимно уничтожаться. Формальное введение фиктивных источ­ника и стока теплоты необходимо лишь для удобства числен­ного определения приращения температуры в период ее вырав­
нивания. Допустим, что спустя время после прекращения действия источника теплоты требуется определить приращение температуры в неподвижной точке пластины А (х, у), координаты которой записаны в движущейся системе координат. За время *ф начало движущейся системы координат переместится в точ­ку О. Приращение температуры точки А определится как раз­ность двух приращений температур: приращения температуры от источника теплоты АТ„, который действовал в течение време­ни t, продвигаясь из точки О о в точку О, и приращения темпера­туры от стока теплоты АТС, который действовал в течение вре­мени /ф на участке ОкО:

АТА = АТК - АТС. (6.36)

Оба приращения температуры АТИ и АТС в уравнении (6.36) можно выразить через приращение температуры предельного состояния и соответствующие коэффициенты теплонасыщения:

дТА = дгпрф2 (0 - ДГпрф2 (/ф) - ЛГпр [ф2 (0 - ф2 (/ф)]. (6.37)

Предельное приращение температуры и коэффициенты тепло­насыщения находят по соответствующим формулам и номо­граммам. Координаты точки А берут обязательно в движущей­ся системе координат, которая продолжает перемещаться со скоростью V.

Если источник теплоты действовал долго и /к велико, т. е. к моменту прекращения нагрева было достигнуто предельное со­стояние, то, следовательно, t — tK /ф также велико и ф2(0 ~ 1. Тогда

АТЛ = ЛГПР [ 1 - ыд]. (6-38)

Последний случай соответствует периоду выравнивания тем­ператур после достижения предельного состояния. Пример был иллюстрирован определением приращения температуры в точ­ке А, принадлежащей пластине. Аналогично вычисляют прира­щения температуры для точек массивного тела и стержня: при этом фз и фь а также ДГпр берут по формулам (6.22) и (6.30).

Пример 6. На поверхность массивного тела из стали, начиная от точки О о (см. рис. 6.12,6), наплавляют валик ОоОк длиной 50 мм. Режим наплавки: эффективная мощность q = 6000 Вт, скорость и = 0,1 см/с. Согласно табл 5.1 а = 0,083 см2/с, X = 0,4 Вг/(см-К). Определить приращения температуры точ­ки Оо в момент окончания наплавки и спустя 30 с после окончания наплавки.

Для расчета принимаем схему точечного источника теплоты, перемещающе­гося по оси Ох на поверхности полубесконечного тела.

Расчет температуры в периоде теплонасыщения в момент окончания свар­ки. Мгновенные координаты точки О0 в момент, когда источник теплоты на­ходится в точке Ок (см. рис. 6.12, б), будут х = — 5 см, у — 0, 2 = 0, R = 5 см. Время действия источника теплоты t = — x/v = 5/0,1 = 50 с. Безразмерные кри­терии расстояния и времени, от которых зависит коэффициент теплонасыще­ния ф3, находят по формулам (6.33):

р3 = Щ?/(2а) = 0,1-5/(2-0,083) = 3; т3 = оЧ/Ца) = 0,12-50/(4-0,083) = 1,5.

По этим данным из графика, изображенного на рис. 6.11. а, находим ф3 = 0,6.

Приращение температуры предельного состояния точки О о, которая имеет мгновенные координаты х = — 5 см, R = 5 см, когда источник теплоты находит­ся в Ок, определяем по уравнению (6.22): АТ„р = 6000/(2-3,14-0,4-5) = 478 К.

Приращение температуры точки О0 в момент окончания наплавки находим по формуле (6.32): АТ = фзЛТ’ир = 0,6-478 = 287 К.

Расчет температуры в периоде выравнивания. Через 30 с после окончания сварки фиктивные источник и сток теплоты будут находиться в точке О (рис. 6 12, б). Отрезок ОкО будет равен vtф = 0,1 -30 = 3 см. Мгновенные коорди­наты точки О о относительно точки О будут х — — 8 см, у = 0, г = 0, R = 8 см.

Длительность действия источника теплоты действительного и фиктивного составит / = 50 + 30 = 80 с. Безразмерные критерии расстояния и времени для источника теплоты по формуле (6 33)

р3 = vR/(2a) = 0,1-8/(2-0,083) = 4,82; т3 = Л/(4а) = 0,12-80/(4-0,083) = 2,41.

По этим данным из графика, изображенного на рис. 6.11, а, находим ф3„ = 0,59. Длительность действия фиктивного стока теплоты равна 30 с.

Безразмерные критерии расстояния и времени для стока теплоты

р3 = 4,82; та = у2//(4а) = 0,12-30/(4-0,083) = 0,903.

По этим данным находим ф3с = 0,03

Предельное приращение температуры точки Оо находим по формуле (6.22): АТ„р = 6000/(2-3,14-0,4-8) = 298 К-

Приращение температуры точки Оо спустя 30 с после окончания наплавки находим по уравнению (6.37):

АТ = Д7;р (ф3„ — ф3с) = 298 (0,59 - 0,03) =167 К.

Пример 7. Для условия примера 6 определить приращение температуры в точке окончания процесса наплавки Ок (рис. 6.12,6) спустя 25 с после прекра­щения наплавки, учитывая, что к моменту окончания процесс достиг предель­ного состояния.

Мгновенные координаты точки Ок относительно точки О: х = — vt^, = = — 0,1 -25 = —- 2,5 см; у = 0; г = 0; R = 2,5 см.

Безразмерные критерии расстояния и времени для фиктивного стока теплоты

рз = vR/{2a) = 0,1-2,5/(2-0,083) = 1,5; т3 = у2//(4 а) = 0,12-25/(4-0,083) = 0,75.

По этим данным из рис. 6.11, а находим ф3с = 0,66.

Предельное приращение температуры точки Ок находим по уравнению (6.12): АТп, = 6000/(2-3,14-0,4-2,5) = 955 К.

Приращение температуры точки Ок спустя 25 с после окончания процесса наплавки находим по формуле (6.38):

АТ = ДГпр (1 - фзс) = 955 (1 - 0,66) = 324 К.