Механика гидро - и пневмоприводов
Течения в коротких каналах с дросселированием потоков рабочих сред
![]() Рассмотрим течение жидкости в канале с дросселирующей поток диафрагмой (рис. 3.1). Исходным для определения характеристик такого течения может служить уравнение (2.52). При установившемся течении последний член в правой части уравнения равен нулю. Если принять для простоты положение оси канала горизонтальным, то, выбрав контрольные сечения а — а и ж — я, из этого уравнения получим
Рассмотрим течение жидкости в канале с дросселирующей поток диафрагмой (рис. 3.1). Исходным для определения характеристик такого течения может служить уравнение (2.52). При установившемся течении последний член в правой части уравнения равен нулю. Если принять для простоты положение оси канала горизонтальным, то, выбрав контрольные сечения а — а и ж — я, из этого уравнения получим
|
В |
![]()
Рис. 3.1. Схема течения жидкости в канале с дросселирующей поток диафрагмой
Г N
|
Кччччччч^Мччч^уХ] 'а х в |
Для сечений х — х и 6 — 6 соответственно имеем:
![]() (3.4)
(3.4)
В уравнения (3.3) и (3.4) входят следующие величины: ра, Рх> Ръ — давления в указанных на рис. 3.1 сечениях; уа, т;*, уь и аа, ах> <*ь — скорости жидкости и коэффициенты кинетической энергии в тех же сечениях; (ах, СхЬ — коэффициенты гидравлических сопротивлений участков между сечениями (а - а) — (х — я) и (ж — х) — (6 — 6).
![]() У реальных дроссельных устройств значения уа и ^ незначительно различаются и каждое из них всегда меньше ух, а коэффициенты кинетической энергии при турбулентных течениях, наиболее частых в таких устройствах, близки к единице. С учетом этих дополнительных допущений по уравнениям (3.3) и (3.4) находим
У реальных дроссельных устройств значения уа и ^ незначительно различаются и каждое из них всегда меньше ух, а коэффициенты кинетической энергии при турбулентных течениях, наиболее частых в таких устройствах, близки к единице. С учетом этих дополнительных допущений по уравнениям (3.3) и (3.4) находим
(3.5)
ГДе Сдр = Сах + СхЬ — коэффициент гидравлического сопротивления короткого канала с дросселированием потока жидкости.
|
5* |
![]() Чтобы вычислить расход фдР жидкости, протекающей по каналу, скорость ух необходимо умножить на площадь 5Х живого сечения потока, которая вследствие сужения потока будет несколько меньше площади 5др проходного сечения дроссельного отверстия. Вводя коэффициент сжатия потока
Чтобы вычислить расход фдР жидкости, протекающей по каналу, скорость ух необходимо умножить на площадь 5Х живого сечения потока, которая вследствие сужения потока будет несколько меньше площади 5др проходного сечения дроссельного отверстия. Вводя коэффициент сжатия потока
(3.6)
Получаем
|
|
Где /лДр = б/ у/Сдр — коэффициент расхода короткого канала с
Установленной в нем дросселирующей поток диафрагмой.
Формула (3.7) является одной из основных среди применяемых в технических приложениях при расчетах разнообразных
Дроссельных устройств. Коэффициент ^др, который входит в эту формулу, обычно принимают по экспериментальным данным, представленным в зависимости от числа Рейнольдса
Хдрі/
Где Хдр — смоченный периметр отверстия (для круглого отверстия диаметром 45др/Хдр = Для прямоугольного отверстия, открываемого кромкой золотника на величину х3 С Ь, Ь — ширина, 45др/Хдр = 2ж3); V — кинематическая вязкость жидкости.
|
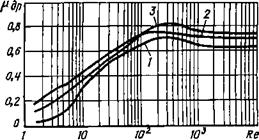
Рис. 3.2. Зависимость коэффициентов расхода дроссельных устройств от числа Рейнольдса |
На рис. 3.2 приведены графики зависимостей /хдр от Ле для круглого отверстия с острой кромкой (кривая 1) и для прямоугольного окна в гильзе гидроаппарата с цилиндрическим золотником, бурты которого имеют острые (кривая 2) и притупленные (кривая 3) кромки. При больших числах Рейнольдса коэффициент расхода отверстия с острой кромкой достигает значения, равного 0,62. Почти такое же значение получено в механике жидкости и газа в результате решения задачи о плоскопараллельном истечении невязкой несжимаемой среды через отверстие с острыми кромками. Это показывает, что коэффициент расхода в основном определяется значением коэффициента сжатия потока после дроссельного отверстия. Данное положение известно из гидравлики и подтверждается также
тем, что при притупленных кромках золотника коэффициент расхода прямоугольных окон несколько выше, чем при острых кромках.
Течения газа в каналах с дросселями отличаются от течений жидкостей из-за более значительного изменения плотности газов в зависимости от давления и вследствие меньшей вязкости газов. Связь между расходом газа и разностью давлений во входном и выходном сечениях канала можно найти с помощью уравнения Бернулли для установившегося движения невязкого совершенного газа. Вычисленные таким способом теоретические значения расхода удается приблизить к действительным, используя экспериментальные коэффициенты расхода. Для газов, учитывая их большую сжимаемость, обычно определяют массовые расходы.
Для баротропного установившегося движения газа уравнение Бернулли выводят из уравнений гидродинамики Эйлера. Пренебрегая объемными силами, представим уравнение в виде
|
|
РО
В случае адиабатического движения невязкого газа зависимость плотности газа от давления описывается соотношени-
Содержащиеся в уравнении (3.10) величины ро и ро выбирают постоянными и соответствующими адиабатически заторможенному газу при V = 0. Из уравнения (3.10) следует формула Сен-Венана и Ванцеля
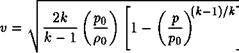 (3.11)
(3.11)
Формула (3.11) определяет скорость V в любом живом сечении потока газа, в котором давление равно р.
Если принять скорость в канале перед дросселем достаточно малой, чтобы в этой области считать газ адиабатически заторможенным, то скорость ух в сечении х — х после дросселя можно вычислить по формуле (3.11), предварительно подставив в нее вместо ро и ро давление ра и плотность ра газа в сечении а — а перед дросселем.
|
(3.12) |
![]() Массовый расход (7др газа на выходе из дросселя равен:
Массовый расход (7др газа на выходе из дросселя равен:
Сдр — Рх1)'г 5®,
Где рх и5х — плотность газа и площадь живого сечения потока на выходе из дросселя.
![]() Согласно соотношению (3.9)
Согласно соотношению (3.9)
(3.13)
Плотность ра зависит от абсолютной температуры 0а газа перед дросселем. Для совершенного газа эта зависимость описывается уравнением Клапейрона
|
Ра — |
![]() (3.14)
(3.14)
Где Д — газовая постоянная, для воздуха равная
287,14 м2/(с2-К).
До тех пор, пока скорость ух не превышает скорость звука в рассматриваемом сечении потока газа, давление рх можно считать равным давлению ръ в канале после дросселя, где, как и до дросселя, будем пренебрегать скоростью движения газа. Используя с учетом сказанного уравнения (3.13) и (3.14), по
Формулам (3.11) и (3.12) нетрудно найти теоретическое выражение для массового расхода через дроссель, умножив которое на коэффициент /хдр расхода, получим
|
, (3.15) |
|
|
К-1 |
|
Ра |
|
— /Хдр5др |
|
У/ |
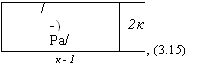 |
|
|
|
Где 5др — площадь проходного сечения дросселя.
Коэффициент /Хдр расхода в формуле (3.15) учитывает как возможное различие значений 5Х и 5др, так и гидравлическое сопротивление канала с дросселем. Этот коэффициент зависит от формы дросселя и режимов течения газа в канале, он может находиться в пределах от 0,6 до 1,0.
При уменьшении давления ръ на выходе из канала до критического значения ркр, при котором скорость V движения газа в сечении х — х или в каком-либо другом сечении потока после дросселя становится равной местной скорости с звука, возникает запирание выходного сечения канала. В этом случае истечение газа происходит с постоянной критической скоростью даже при дальнейшем уменьшении давления Критерием смены режимов движения газа служит число Маха
Ма = —. (3.16)
С
Если Ма < 1, то движение газа дозвуковое, если Ма > 1, то движение газа сверхзвуковое, при Ма = 1 имеем рь = ркр. Критические параметры ркр, 0кр, скр, рКр вычисляют с помощью параметров ра, 0а, са, ра заторможенного газа, используя соотношения:
К
0*
|
Ркр _ Ра |
![]() К - 1
К - 1
/кр * .
|
К + 1 |
![]() 0а к+11
0а к+11
1
|
К-1 |
![]() Скр __ / 2 рКр ^
Скр __ / 2 рКр ^
|
К+1 |
![]() Са V к + 1 ’ Ра
Са V к + 1 ’ Ра
В соответствии с первым из этих четырех соотношений условие, при выполнении которого движение газа будет дозвуковым
И справедлива формула (3.15), имеет вид
К
|
(3.17) |
Ра [к + 1
Для воздуха к = 1,4, поэтому течение является дозвуковым, если
— > 0,528. Ра
Оценка влияния сжимаемости газа на значения расхода показывает, что при Ма <0,14 ошибка не превысит 1 %, если расход вычислен как для несжимаемой жидкости.
При (рь/ра) < (Ркр/Ра) массовый расход газа через дроссель определяется соотношением
|
|
(3.18)
|
(3.19) |
![]() Сд — ^, Рд — Рай®а
Сд — ^, Рд — Рай®а
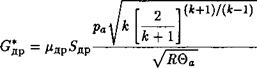 Формулу (3.18) можно привести к виду
Формулу (3.18) можно привести к виду
(3.20)
Формула (3.20) показывает, что в данном случае массовый расход газа через дроссель не зависит от давления рь на выходе из канала, а изменяется только при увеличении или уменьшении давления ра на входе в канал.
![]() Разделив формулу (3.15) на (3.20), получим
Разделив формулу (3.15) на (3.20), получим
(3.21)
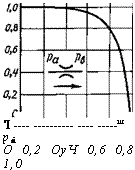
![]() С помощью функции (3.21), график которой показан на рис. 3.3, массовый расход газа через дроссель можно вычислять по формуле
С помощью функции (3.21), график которой показан на рис. 3.3, массовый расход газа через дроссель можно вычислять по формуле
(3.22)
Рис. 3.3. График функции для расчета массового расхода газа через дроссель
|
'I-------------------------- ш рй О 0,2 ОуЧ 0,6 0,8 1,0 |
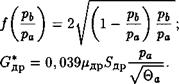 Для воздуха Л. Прандтль предложил приближенные формулы, которые представим в виде
Для воздуха Л. Прандтль предложил приближенные формулы, которые представим в виде
Явление, аналогичное запиранию канала с дросселем при критическом истечении газа, наблюдается и при течении жидкости в канале с жиклером в виде цилиндрического насадка. В таком жиклере после снижения давления в сжатом сечении потока до значения, близкого к давлению насыщенных паров жидкости, возникает кавитация, которая сопровождается отрывом потока от стенок жиклера. При последующем увеличении давления на выходе из канала расход жидкости не изменяется до тех пор, пока это давление не станет равным приблизительно половине давления на входе в канал.