Оптоэлектроника

Шум и ширина полосы лазерного диода

Вы видели в дополнении 4. Г, каким образом спонтанная эмиссия, будучи результа­том квантового перехода и, таким образом, непредсказуемой, может быть представ­лена в рамках динамических лазерных уравнений виде ланжевеновских сил. Эти силы являются хаотичными временными процессами (или стохастическими про­цессами), обладающими амплитудой автокорреляционной функции вследствии со­гласования (смотрите 4.Г.126) динамических уравнений (4.Г. З) со скоростными уравнениями (4.А. 13). В этом последнем случае спонтанная эмиссия учитывается заменой члена эмиссии e'er sn на член e'er (5 + 1 )п. Таким образом, для переменных случайной амплитуды / и (£азы ф получаются два несвязанные дифференциальные уравнения (смотрите (4.Г.15)). Тот же самый формализм может быть использован и в случае лазерных диодов. Однако, в этом случае рассчитанная спектральная полу­ширина оказывается намного уже наблюдаемой экспериментально. Этот феномен был успешно объяснен С. Генри, заметившим, что полупроводниковый лазерный
диод является рассогласованным лазерным резонатором из-за того, что случайные переменные амплитуды и фазы коррелируют друг с другом за счет связанных измене­ний усиления и коэффициента оптического преломления. Другими словами, флуктуа­ции коэффициента оптического преломления полупроводника также приводят к флуктуациям резонансной волны резонатора, что обуславливает уширение лазер­ной линии. Этот эффект является уникальным для полупроводниковых материа­лов. Наш анализ продолжим рассмотрением модели С. Генри.

Предчувствуя важность влияния относительной проницаемости на распростра­нение электромагнитного поля, мы более не можем ограничиваться изучением элек­тромагнитных флуктуаций в одной точке (например, при * = 0), как это имело место в (4.Г. З). Таким образом, начнем с описания электромагнитного поля с ис­пользованием понятия случайной нестационарной огибающей (смотрите 4.Г.14)):

Е(1, 0= £(г)е'(ь-') (13.Ж.1)

Будем искать уравнение Ланжевена для лазерной среды с относительной про­ницаемостью е, которому эта нестационарная огибающая может удовлетворять. Запишем волновое уравнение:

(13.Ж.2)

В рамках аппроксимации нестационарной огибающей функции членом д1Е1дг1 можно пренебречь, при этом (13.Ж.1) и (13.Ж.2) приводят к:

Е(()=-(^£х-1с2)е(г) (И. Ж.З)

Здесь, по определению, относительная проницаемость еж есть:

У (13.Ж.4)

Параметры пж и п1т обозначают соответственно действительную и мнимую части

Коэффициентов преломления. Действительная часть коэффициента преломления связана с коэффициентом распространения к выражением:

К = ®п^ = ® (13.Ж.5)

С с

Мнимая часть коэффициента п1т описывает затухание амплитуды волны в по­лупроводниковой среде. Коэффициент поглощения, определяемый (3.36) в этом случае может быть записан в виде:

® = 2 —и, т (13.Ж.6)

С

(Напоминаем, что в данном случае амплитуда будет изменяться как е_а/2*, а мощ­ность как е_ог).

В лазерной среде эффективный коэффициент поглощения а в действительнос­ти является результатом конкуренции, с одной стороны, между паразитным погло­щением ар и потерями на зеркалах ат(ат = — /2Ьп(ЯхЯ) и ас = ар +ат, а с другой стороны — усилением Т'так, что:

-*■,= (13.Ж.7)

С 2

У лазерного порога усиление уравновешивает потери так, что п1т = 0 и коэффи­циент оптического поглощения становится чисто действительным. Несмотря на это, флуктуации числа носителей Ап приводят к флуктуациям проницаемости £, что описывается соотношением:

£* = ("вс + Ди* + «АИщ. )2 “ я* + 2ЧДи|т(1 - Фс) (13.Ж.8)

Здесь Яe есть коэффициент уширения, определяемый соотношением:

А=Т5л - (13.Ж.9)

^Пт

Коэффициент уширения

Подставляя выражение для (13.Ж.8) в уравнение (13.Ж. Э), используя (13.Ж.5) и сохраняя только члены первого порядка, мы находим, что огибающая функция E(t) является решением дифференциального уравнения:

■%-E(t)=-<o^baLb-iЯ')E(f) (13.Ж.10)

Dt пж

Это уравнение может быть также записано в виде:

^E(t)+±c'(ac-rXl-iЯe)E(t)= О (13.Ж.11)

Читатель легко узнает это уравнение, поскольку оно идентично (4.Г. З), в кото­ром пренебрегалось влиянием флуктуаций на проницаемость ех, за исключением дополнительного коэффициента умножения (1 — iЯe), который учитывает флуктуа­ции €к.

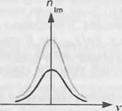
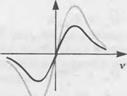
Коэффициент Яe равен нулю для атомных переходов, как это имеет место в данном случае; лазерная генерация имеет место в пике лоренцовской кривой уси­ления, где Апк равно нулю (смотрите рис. 13.Ж.1). Соотношение Крамерса—Кро - нига утверждает, что действительная часть коэффициента преломления Пк пропор­циональна производной коэффициента поглощения, что само по себе связано с П1т. С другой стороны, в конденсированных средах кривая усиления более не носит лоренцовский характер и даже в максимуме усиления Апк не равно нулю (смотрите рис. 13.Ж.1).

SHAPE \* MERGEFORMAT

-------- л/

N +Д4

А б

Рис. 13.Ж.1. В атомных системах изменение коэффициента оптического преломления в функции концентрации носителей AnR/AN равно нулю с учетом лорен­цовской кривой усиления (а). В полупроводниковой среде кривая усиле­ния асимметрична, при этом Алк/АА^не равно нулю, что приводит к не­нулевому коэффициенту уширения линии излучения Апя/Ап1т.

В соответствии с формализмом, развитым в дополнении 4. Г. введем ланжеве - новскую силу возбуждающую электрическое поле в соответствии с

Соотношением:

— £(/)+ - с'(ас -у){ - реЩ)= НО (13.Ж.12)

Э/2 2

Вводя подобно дополнению 4. Г, интенсивность / и фазу ф, мы можем разделить это дифференциальное уравнение на два:

— / + с'(ас - уУ = 2ЛЯе[^ (/)е'*] (13.Ж.13а)

<3/

^Ф~{П-гЖ = /;(/) (13.Ж.136)

Теперь добавим к этим уравнениям изменение числа носителей п и возвратимся к обозначениям, введенным в дополнении 13.Е. (смотрите рис. 13.Е.2). При этом мы получаем ланжевеновские уравнения для полупроводниковой лазерной среды:

- (г# - у,> + = РХО (13.Ж. 14а)

±Ф-{Ъ~ГЖ = РФ(!) (13.Ж.146)

^Ln + rmn + Gs=-L±J + Fn(t) (13.Ж.14в)

Ш да а/

Лаежевеновские уравнения для полупроводникового лазера

В дополнение к (4.Г. 15) мы добавили к динамическому уравнению для числа фотонов 5 (13.Ж. 14а) детерминистский член спонтанной рекомбинации /?8роп та­ким образом, чтобы среднее значение члена (/^(0) было равно нулю. Этот член Яроп (см_3) есть скорость излучательной рекомбинации, полученная в разделе 7.5 и уже введенная в дополнении 13.Д: Язроп = /ЗВпр = Рп/тгаа, где В есть коэффици­ент излучательной рекомбинации, ггас1 — излучательное время жизни (смотрите уравнение (7.61)), а /3 есть коэффициент спонтанной эмиссии (смотрите допол­нение 13.Е).

Нам по-прежнему необходимо определить автокорреляционные функции для ланжевеновских функций /’Д/), ^,(0 и /’(О. Процедура расчета в данном случае такая же, как и та, что использовалась в дополнении 4.Г. Поскольку их вывод достаточно сложен, мы ограничимся итоговыми результатами:

(Г. ЪУЛ’Ъ = 2ДЖ' - О; О. = /^п * (13.Ж.15*)

(гЛУЛ') = 2/>.*</ - О; От = /?5ро„ 5 + У,„п (13.Ж.156) {р. ЬУЛ'Ъ* 2- /'); (13.Ж.15«)

4 5

Здесь мы пренебрегли перекрестными членами по Г>5п. Достаточно полное описа­ние этого последнего расчета можно найти в работе С. Генри (1982).