Оптоэлектроника

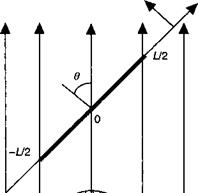
Влияние угла падения

Принцип в основе этого расчета идентичен тому, который был представлен для случая объемного полупроводника (смотрите уравнение (7.42)) с добавлением ряда тонких моментов для учета двумерной природы квантово-размерной системы. Мы могли бы поинтересоваться, почему следует ожидать, что коэффициент поглоще­ния будет изменяться в зависимости от того, падает ли излучение перпендикулярно или под углом к квантовой яме. Сейчас мы представим детальное описание меха­низмов поглощения излучения, имеющих место в квантовой яме.

Баланасная скорость перехода <7(см-2 с-1) соответствует поглощенной мощности IV электромагнитной волны, равной:

IV

= НсоС [Вт см 2]

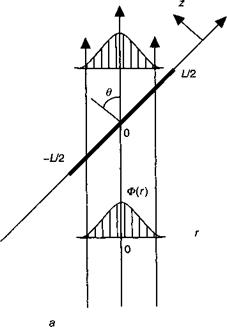
Среда, содержащая квантовую яму, является по сути неизотропной. Для расчета поглощения, испытываемого волной, проходящей через среду, мы, таким образом, должны учесть геометрию и пространственную протяженность пучка излучения (смотрите рис. 8.18).

Рис. 8.18 иллюстрирует общий случай. Плоская волна с распределением потока, опре­деляемым Ф(г), встречает на своем пути квантовую яму, перекрывающую угол в по отношению к направлению распространения. В этом случае амплитуда электричес­кого поля определяется соотношением:

(8.79)

Здесь: п(со) есть коэффициент преломления и70 = есть вакуумный импе­

Данс. Энергия, пересекающая структуру за одну секунду составляет:

(8.80)

Х

О

Рис. 8.18. Электромагнитная волна с распределением интенсивности Ф(г) распростра­няется через среду и встречает на своем пути квантовую яму длиной Ь, ори­ентированную под углом в к направлению распространения.

Полная скорость поглощения в квантовой яме, нормированная на энергию па­дающего излучения Ж, в этом случаен составляет:

У&6 / 2 | ф(г)сіг

(8.81)

Ж.

Отметим, что ширина ямы в явном виде не входит в это выражение для поглоще­ния. Скорость поглощения не зависит от ширины ямы и является безразмерной (выра­женная в процентах). С другой стороны, угол 0входит в (8.82) и также в выражение для скорости перехода <7 в соответствии с правилами отбора, приведенными в Таблице 8.1. 2. Если перетяжка пучка излучения велика, что, в частности, имеет место в случае в = л/2, и интенсивность не изменяется в яме, поглощение составляет:

ЬсоС[Е (0)] Г

Ф(0)

Здесь мы ввели коэффициент ограничения:

Г 1Е,(0)Г<У

||Е,(г)|2с1г

Где £/ есть толщина ямы, а Г есть доля волны, которая «видит» поглощающую среду.

В этой геометрии представляется естественным ввести коэффициент поглощения кван­товой ямы с использованием выражения:

(8.85)

Коэффициент поглощения для параллельного распространения в яме

Сейчас мы уже можем рассчитать коэффициент поглощения с использова­нием выражений для скоростей различных переходов (7, которые мы установили в

(8.75) для межподзонных переходов.

Начнем с межзонных переходов. С учетом выражений (8.65), (8.79) и (8.82) поглоще­ние для квантовой ямы дается вкладами переходов, связанных с участием различ­ных пар участвующих подзон:

«о* = X - ест - |г; )/; (Псо)-(йа>)] (8.86а)

При этом коэффициенты поглощения для каждого перехода (смотрите уравнение

(8.75) составляют:

(8.866)

Вклад межзонных переходов л -> т для поглощения квантовой ямы (%)

В случае межподзонных переходов поглощение между переходами с участием различ­ных подзон описывается соотношением:

(8.87л)

Это дает для каждого перехода (смотрите (8.75)):

(Пп -ПтУ>{£т ~£п - Ь0>) (8.87б)

Вклад от межподзонных переходов л -> т в поглощение квантовой ямы (%)

В этом последнем выражении, как мы напоминаем, 3 есть 3-функция, выра­женная в Дж“1, которая может быть заменена на лоренциан, если переход уширен по какой - то особой причине. Более того, мы отмечаем, что г]д1 = Е?/|£ | есть вектор поляризации электромагнитной волны и г] = ь'тв — его компонента вдоль оси роста квантовой ямы. При п = 1 и т = 2 (8.876) идентично соотношениям (3.37) и (3.39) для оптического поглощения в двухуровневой системе, полученным с ис­пользованием формализма матрицы плотности. Это подчеркивает глубокую анало­гию между внутриподзонными переходами в полупроводниках и переходами в атом­ной физике.

В соотношениях (8.86б) и (8.87б) мы видим существенно различный характер угловой зависимости для каждого из этих типов механизмов. Более примечатель­
ным является то, что межподзонное поглощение раскрывает характеристическую зависимость от вт2# и, таким образом, оно характеризуется нулевым значением при нормальном падении (0=0). Как мы увидим позже в главе 11, это имеет очень важные последствия для квантово-размерных фотодетекторов.

Пример-------------------------------------------------------------------------------------------------------------

1. Межподзонное поглощение в квантовой яме ваАБ.

Для фундаментальных переходов кк—е[ в квантовой яме ваАз мы можем считать пе­рекрытие огибающих функций равным единице. Для электромагнитной волны, падаю­щей по нормали к квантовой яме межзонное поглощение дается формулой (8.866) и мы находим для Ь со=1,5 эВ:

Tiax^m, Zq_|^ г |2 _ 1,5 эВх0,059x9,1x10 31 кг 377 0м

Пг Ти©1 * "I (б,58х10"16 эВс)3 4п [Л

Здесь мы использовали правила отбора из таблицы 8.1, а тсу величина объемного поглощения, приведенная в таблице 7.1.

2. Межподзонное поглощение в квантовой яме ваАз.

Рассмотрим глубокую квантовую яму ваАБ, позволяющую нам аппроксимиро­вать низко лежащие состояния бесконечной прямоугольной ямой той же ширины. Предположим, что ширина и уровень легирования ям составляют соответственно 10 нм и 1012 см~2, при этом температура достаточно низка так, чтобы занятым был только основной уровень. Зазор между двумя уровнями вблизи дна ямы дается со­отношением (1.49) или:

Еп = (4 - 1)-^1 = I-------------- (л - х_1,05 х_]0_* Джс)^ _ = ,69 мэВ

2тса2 2 0,067 х 0,9 х Ю"30 кг х (ю-8 м)

Дипольный матричный элемент определяется соотношением (З. Г.24):

|(11*| 2)| = - Д-Та = 0,18л = 1,8 нм (Злг)

И наконец, межподзонное поглощение в резонансе для волны, падающей под углом 45°, дается выражением (8.876). Предполагая уширение НГ, равным 10 мэВ, заменим ^функцию на 1/(яНГ) так, что:

N^m _ 1 ^CЬ Z0

QW

Ti hY n(co)

J______ 0,169;; 377Om _ (l,6x!0~19 Cxl,8xl0~9 uf 1Q|6 м-2 =8х10-з

1.05x10 Джс 0.01 3.3