Проблемы, накладываемые континуумом: виртуальный квантовый ящик и плотность состояний
Квантовое описание делокализованных состояний, принадлежащих континууму, использует теорию распределений. Это описание пытается дать трактовку сложных проблем, таких как нормировка волновых функций в нулевом потенциале в интервале от —о® до +оо. в этой книге систематически используется прием, основанный на введении понятия виртуальной бесконечной квадратной ямы шириной L, в которой движение электронов континуума, как мы увидиим дальше, является квази-кванто - ванным. Более того, когда мы принимаем L, стремящимся к бесконечности в полученных выражениях, зависимость от L удобным образом исчезает из наших физических предсказаний. В этих рассуждениях нет никакого дополнительного поучения; разве что педагогическая защита теории распределений! Далее рассмотрим иллюстрирующий пример: фотоэмиссию из одномерной ямы.
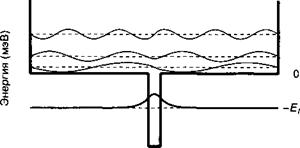
Рассмотрим квантовую яму шириной L, как это представлено на рис. 1.А.1.
|
L
|
Положение (нм)
Рис. 1.А.1. Процедура квази-квантования состояний потенциального барьера. Ширина Ь бесконечной квадратной ямы имеет произвольную величину.
Эта квантовая яма допускает существование квантового уровня |/), описываемого квадратично интегрируемой волновой функцией и квантовым энергетическим уровнем — Е1 (где индекс / соответствует (по причинам, которые будут понятны позже) ионизации). Далее мы предположим, что яма достаточно глубока для ), чтобы рассматривать в качестве волновой функции основного состояния функцию вида:
Г1к)=^С08^* (1.А.1)
Эта яма допускает существование делокализованных состояний, в которых электроны могут иметь любую положительную величину энергии. Мы будем пренебрегать влиянием ямы на свободные электроны, т. е. будем предполагать, что свободные электроны подвержены воздействию нулевого потенциала, как только они оказались в области континуума. Во избежание проблем, связанных с нормировкой этих волновых функций, мы вводим виртуальную квадратную яму шириной Ь, внутри которой электроны континуума являются захваченными. Соответствующие собственные энергии и собственные функции несвязанных состояний имеют вид:
|
Sin nkLz, если п является четным (1.А.2) |
![]() Cos nkLz, если п является нечетным энергия ограничения виртуальной ямы:
Cos nkLz, если п является нечетным энергия ограничения виртуальной ямы:
Ео = - т~т Щ. (1.А. З)
|
С волновым вектором к |
![]()
|
L' |
![]() 2т
2т
^ = у (1.А.4)
Если Ь имеет сантиметровые размеры, то е0 имеет величину порядка 10-11 эВ. В этом смысле такой ящик был бы виртуальным, так как энергетический интервал между уровнями был исчезающе мал по сравнению энергией тепловых взаимодействий (порядка мэВ). Энергетические уровни в соответствии с (1.А.2) настолько близки друг к другу, что вместо того, чтобы пытаться рассматривать их по отдельности, сгруппируем их вместе с помощью бесконечно малых секторов плотности состояний.
Рассмотрим некий интервал волнового вектора йк. В пределах этого интервала отдельные состояния виртуального ящика разделены по волновому вектору на р/Ь. Очевидно, что без учета электронного спина число состояний в пределах этого интервала составляет:
Йп = — йк (1.А.5)
71
В этом случае плотность состояний йп/йк дается соотношением:
Р(*) = - ТГ = - (1А6)
6к п
Дифференцированием (1.А. З) получаем, что в том же интервале соответствующее изменение энергии связано с йк соотношением:
(1.А.7)
В результате энергетическая плотность состояний принимает вид:
I л]2т* 1 , 0
Одномерная плотность состояний без учета спина
Отметим, что при стремлении Ь к бесконечности, р (Е) также будет возрастать без ограничений. Этого и следовало ожидать, так как все большее число состояний будет находиться в пределах одного энергетического интервала, когда энергетический интервал между состояниями уменьшается.
Теперь рассчитаем вероятность перехода между начальным квантовым состоянием |/) и континуумом в условиях синусоидально изменяющегося дипольного возмущения:
Щ. Z,i)=: -qFzcos(wf) (1.А.9)
В соответствии с золотым правилом Ферми (1.856) вероятность перехода может быть записана в виде:
|
(I. A. 10) |
![]()
|
I. A. Проблемы, Накладываемые континуумом 39 |
![]() G*(ftЯ>) = ^p~zf2p{hco =Е,- £,)
G*(ftЯ>) = ^p~zf2p{hco =Е,- £,)
Матричный элемент перехода ^ отличен от нуля только для нечетных конечных состояний и дается выражением:
SHAPE \* MERGEFORMAT ![]()
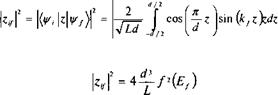
|
Или |
![]() (1.А.11)
(1.А.11)
|
И kf— волновой вектор соответствующего состояния с энергией Е'Г |
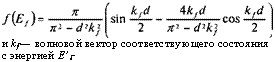 Где/(£) представляет собой одномерный интеграл в уравнении (1.А.11), выражающийся соотношением:
Где/(£) представляет собой одномерный интеграл в уравнении (1.А.11), выражающийся соотношением:
(1.А.13)
|
|
(1.А.14)
Теперь подставим выражение для zif в (1.А.10). Заметьте, что, как и предсказывалось, ширина виртуального ящика L, которая фигурирует в знаменателе матричного элемента перехода и числителе плотности состояний, в этом случае устраняется. С физической точки зрения, чем больше ширина квази-ямы, тем больше должна быть плотность конечных состояний. Однако влияние этого фактора на вероятность перехода устраняется, так как увеличивающаяся ширина приводит также и к уменьшению плотности вероятности электронных состояний над квантовой ямой (шириной L) на подобную же величину.
Учитывая, что плотность конечных состояний составляет лишь половину выражения, представленного в виде (1.А.8) (вследствие спина электронов, сохраняющегося в процессе переходов), мы находим таким образом, что вероятность перехода из начального квантового состояния в континуум может быть записана в виде:
|
ЛГт* f2(hco-El) ~И2 |
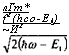
![]() (1.А.15)
(1.А.15)
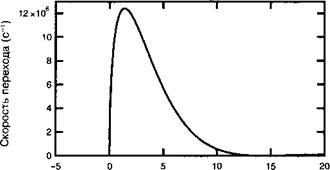
Таким образом, мы обнаружили, что поведение системы не зависит от размера виртуального ящика, введенного нами первоначально. Этот метод называется методом квази-квантования, и он оказывается мощным инструментом несмотря на свою кажущуюся простоту. Рисунок 1.А.2 иллюстрирует зависимость скорости перехода от частоты возбуждения со.
Обратите внимание на наличие порога ионизации для вероятности перехода. Энергия среза для детектируемых фотонов соответствует энергии ионизации. Более того, поглощение вблизи порога детектирования, т. е. для фотонов с Н со ~ Ер дается соотношением:
|
(I. A. 16) |
![]() Gif ос ^fico-En дляНсо - Ef
Gif ос ^fico-En дляНсо - Ef
Второй особенностью является квази-резонансная природа вероятности перехода вблизи энергетического порога фотоионизации. Этот квази-резонанс возникает как следствие уменьшения плотности состояний (как к~1) также и дипольного момента (как к.~2), что приводит к:
|
Энергия фотона, приведенная к Е( Рис. 1.А.2. Зависимость скорости ионизационных переходов (с-1) в квантовой яме от энергии падающих фотонов, нормированной на энергию ионизации, Ег |
0 7--------- —*7Т> пляпсо» Е1 (1.А.17)
^(о-Е1),~
Приведенные выражения дают разумное описание спектральной характеристики квантово-размерных детекторов.