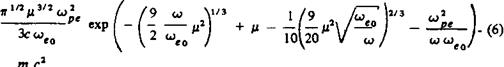ФИЗИКА ПЛАЗМЫ

10 августа 1983 г. О ЦИКЛОТРОННОМ ИЗЛУЧЕНИИ ПЛОТНОЙ ПЛАЗМЫ

А. В. Тимофеев

Отмечено, что циклотронное излучение высокотемпературной плазмы определяется ре­лятивистским "хвостом” функции распределения электронов по энергиям, т. е. по суще­ству является синхротронным. Показано, что эффект депрессии синхротронного излучения может существенно уменьшить излучение плазмы, если ее плотность достаточно велика.

1. В 1 было показано, что магнитотормоэное излучение релятивистских частиц (синхро - тронное излучение) резко ослабляется, если они движутся не в вакууме, а в плазме доста­точно высокой плотности. Это явление хорошо известно в астрофизике, где оно называет - ся депрессией синхротронного излучения, см., например, 2. В настоящем сообщении найде­но, что эффект депрессии может существенно (в нвскэдысо раз) уменьшить излучение высо­котемпературной плазмы (7^25 кэВ).

2. В соответствии с законом Кирхгофа плотность потока излучения плазмы (Dl/DcjdCl сла­

Бо отличается от равновесной - рэлей-джинсовской, если коэффициент поглощения излуче­ния, падающего на плазму - t?(cj, 12), близок к единице. Для плазмы с параметрами L > Р 1 м, 7*> 25 кэВ имеем 17(a) ( 12)** 1 при ~ и *?(w, 12)« 1 при

W Здесь а) * - так называемая высвечиваемая частота. Соответственно полное излу­

Чение плазмы приближенно дается выражением

I = CJ*3Т/12я*с2 .

Здесь учтены колебания одной поляризации (необыкновенные), уносящие основную долю энергии из плазмы. В 3 показано, что точность расчета излучения получается неплохой, если частоту а>* определять из равенства

2#с(о)*, 0 = тг /2)1 = 1, (1)

/ч

Где К — коэффициент пространственного затухания, В = кВ0. Для слоя плазмы толщиной L имеем 17 = 1 — ехр( — 2KL).

Найдем k(cj, ,6 = тг/2) с учетом эффекта депрессии. При вычислении К используем со­отношение Эйнштейна между излучательной и поглощательной способностями плазмы, ко­торое в классическом пределе (hw « Т) принимает вид, см., например,4 :

4тг3с2 Dj Dfo

К --------------- р (2)

A) acjal2 De

Где (dj/dbj)dSl — излучательная способность отделъноцр электрона.

Синхротронное излучение ’’формируется” за время At « a>” 1 • Поэтому его удобно рассчитывать как тормозное, возникающее при ’’столкновении” электрона с магнитным полем, см.,например, 5’6-:

Dj Е* Cj Со

—------- = ------------- Е IJ I 2

DudO. (2тг )3с2

Оо

J * / Dt v(t) exp (1 a> T - Ikj(t)). (3)

- 00

Здесь время отсчитывается от момсяга, в который ▼ W II к.

Для необыкновенных колебаний, распространяющихся поперек магнитного поля

Оо

J « Ь>е / Dt T exp (/ Ф(T), W

- 00

Где ФМ“ <•>*- *• (ы-Ли. у + ^-кре{ш^)г - -^- Кре(шег)5, Ре = —.Пред-

3. 5. ТЕ^ео

Положим, что из всего максвелловского распределения по скоростям определяющий вклад

В излучение дают электроны, скорость которых близка к скорости света и **

( 1 / Т.с2 3/т Л4 и1

* С! 1------- ( —— I + -/—- I 1, а питч-угол X - агсtg— близок к В = 7г/2. Будем счи -

2 р / 8 р / / иц

Тать также, что плотность плазмы не слиццсом высока (<*>ре « а> ), при этом К «

« - ( - ^(-^1 При этих предположениях-получаем

Ф

(5)

+ - 6

Здесь использовано соотношение

Где = ЕВ0/тс. Интеграл по Л в (4) вычисляется методом перевала

СО С

Подставляя последнее выражение в (3) и (2) и используя метод перевала также для интег­рирования по Йе и С1х .получаем

/4 ы 1/3 1

Здесь Ц = — >> 1. Точка перевала расположена при Р «[----------------------- тасГ) — — X

Г 13 ыл е / Ю

/3 О) V'5

X I — ~г ) т*е* с53 * Выражение (6) отличается от полученного в 7 последним слага­емым в показателе экспоненты, которое и учитывает эффект депрессии. Соответствие (6) результату работы 7 показывает, что предположение об определяющей роли высокоэнер­гичных электронов в излучении было правильным.

3. Используем (6) для определения максимальной высвечиваемой частоты. В условие (1) входят безразмерные величины Л = <*>9Ць>€йС, Ц = Тес2/Т= (<^реЛ^ео)2, л = и/сов0.

Представим П* = 0в функции от &еВЬ (Гс*см) = Щ-АТ (кэВ), рассматри­

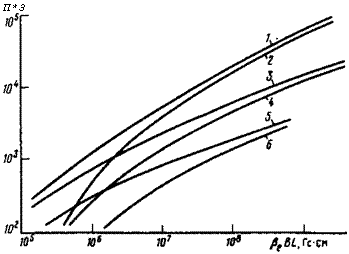
Вая д, как параметры. При =0 из (1) получаем результаты 3' 7”*. (Неточность расчета не превышает неточности аппроксимационных формул, полученных в *). При Це - = 10 эффект депрессии может уменьшить излучение в несколько раз, см. рис. 1. Влияние этого эффекта резко возрастает при увеличении плотности плазмы, см. рис. 2.

Рис. 1 и рис. 2 показывают, что эффект депрессии может значительно уменьшить цикло -

Тс2

Тронное излучение при Яе = 0е “~2Т~ ^ 10* 1^клотРонное излучение играет существенную

Роль в энергобалансе высокотемпературной плазмы (Г 25 кэВ). В этом случае условие ^ ^ 10 может быть выполнено лишь при достаточно высоком давлении плазмы 0 =

= 8тТ0Т^/В2 5$ 1. Такое соотношение параметров характерно для так называемых компакт­ных торов.

Рис. 1. Зависимость номера максималь­ной высвечиваемой гармоники от 0еВ1 При различных значениях плотности плазмы и температуры. Кривая 1 - Т=

* 100 кэВ, <7Е * 0; 2 - Г * 100 кэВ, *

* 10; З'—'Т* 50 кэВ, Яея0,4 - Г =50кэ^ <7е*10;5-Г-25 кэВ,^»0; 6- Т = *25 кэВ,<?е - 10

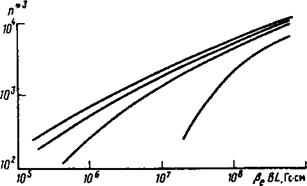
Рис. 2. То же, что на рис. 1 при Т = 50кэВ и различных значениях плотности плаз - мы. Кривая 1 - Д£ = 0; 2 - яе = 3 ,3 - Яе - Ю; 4 - де ■

30

В ряде систем (бампи-торы, модифицированные амбиполярные ловушки и т. д.) элек­тронная компонента плазмы состоит из двух частей - основной с температурой Те « тес2 И небольшой группы высокоэнергичных электронов с € ^ Тес2. В таких системах эффект депрессии будет существенно снижать синхротронное излучение высокоэнергичных электро­нов при Изре >, иео €/т с2, где Ь)ре -ленгмюровская частота "холодных” электронов, см.,1 • а также 2’5. (Этое условие легко получить, анализируя состояние фазового резонан­са между высокоэнергячными электронами и электромагнитными колебаниями, характери­зуемое фазой (5) ). Например, в условиях эксперимента 10 величина для депрессии синхротрокного излучения должна быть увеличила примерно в десять раз.