ЭЛЕКТРОННЫЙ ЦИКЛОТРОННЫЙ РЕЗОНАНС В НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Л. В. ТИМОФЕЕВ, Г. Н. ЧУЛКОВ Введение
Неоднородность магнитного поля ограничивает область резонансного циклотронного взаимодействия и поэтому является одним из основных факторов, определяющих его интенсивность. Влияние неоднородности существенно зависит от угла между магнитным полем Н0 и его градиентом VН0. Дело в том, что от значения этого угла зависит, под каким углом 0 к магнитному полю подойдет волна к точке циклотронного резонанса. Если г£=0, то для одной из двух высокочастотных ветвей колебаний, а именно для необыкновенных колебаний, оказывается равным нулю и угол 0 [*]. В точке циклотронного резонанса электрическое поле таких колебаний перпендикулярно основному магнитному и вращается в электронную сторону (см., например, [2]). Естественно, что такие колебания весьма интенсивно взаимодействуют с электронами [3*4].
Если 1|э=0, то для обеих ветвей колебаний в точке циклотронного резонанса отличен от нуля и угол 0. Между тем известно (см., например, [2]), что в плазме с холодными электронами (7’,=0) достаточно любого, как угодно малого отклонения волнового вектора к от направления Н0, чтобы электрический вектор стал вращаться в обратную, т. е. ионную сторону. В результате при 0=^0 резонансное циклотронное взаимодействие всецело обусловлено эффектами теплового движения электронов и поэтому оказывается довольно слабым. Параметр, характеризующий влияние тепловых эффектов на колебания, пропорционален малому отношению (Ие/с)2, где Ие=(Тв/тв)Чг (см., например, [5]).
Резонансное циклотронное взаимодействие в неоднородном магнитном поле при рассматривалось в работах [в~8] в связи с проблемой нагрева плазмы в токамаках. Интенсивность нагрева определяется значением коэффициента поглощения колебаний при их прохождении через область циклотронного резонанса. Для магнитного поля токамаков |г~л/2. при этом значении угла 1|э и вычислялся коэффициент поглощения в [в~8]. В настоящей работе получено компактное аналитическое выражение для коэффициента поглощения колебаний при произвольных значениях углов 1|) и 0. Показано, что оно остается справедливым вне зависимости от величины градиента магнитного поля. Рассмотрение проведено несколькими способами. В частности, решено интегральное уравнение, которое описывает резонансное циклотронное взаимодействие в сильнонеоднородном магнитном поле.
А. Дисперсионное уравнение. Рассмотрим электромагнитные колебания, частота которых ю близка к электронной циклотронной а длина волны значительно превышает электронный ларморовский радиус ре®*
|
X(l+iVnM? W(M>)), значок «поперечно» отмечает компоненту, перпендикулярную основному магнитному полю. Приравнивая нулю определитель системы уравнений (1), можно получить - дисперсионное уравнение рассматриваемых колебаний в том виде, в котором оно приведено в [5] (см. также [*“*]). Однако рис | это представление дисперсионного уравне Ния неудобно для использования ввиду его громоздкости. Чтобы привести дисперсионное уравнение к более простому виду, воспользуемся тем, что в определителе системы (1) элемент ац^е^'сого/Лхі;, значительно превосходит все остальные. (Здесь и в дальнейшем при оценках считаем G~Nz~N±~ 1.) Отметим, что на использовании этого обстоятельства основан анализ дисперсионного уравнения, проводимый в [5~8]. Приравнивая нулю алгебраическое дополнение А1и в первом порядке по большому параметру (A/Kzue получаем Ло=л4 sin2 0—/г2(2(1—д) +sin2 0) + (2-д) (-д) =0. (2) Используя (2) при вычислении определителя системы (1), приводим полное дисперсное уравнение к виду (пг+тд"і) |
|
/1 Л 1 11 ^ +8»] в**. ^п2п±е-^, — уП±1+уе„ Здесь П=кс/го — показатель преломления, е^^вхх+івх^Зіо-М, в(Х) = Роятности от комплексного аргумента 1 - - |
|
(3) |
|
=0. |
|
■*JL |
|
Го—го. |
|
, (п24-2д— 1)г. со—со* |
|
+ІО - |
|
4 (п±2+д— 1) го ^ (я^+д—1) Метод последовательных приближений по малым параметрам К, ив/<ау , использованный при выводе дисперсионного уравнения (3), |
|
У^х«,ф |
|
-л*+тп^ + е« |
|
|
|
|
|
|
|
|
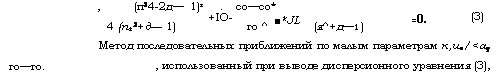 |
|
|
|
|
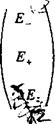
6. Эффекты теплового движения электронов и поглощение колебаний. Колебания, описываемые дисперсионными уравнениями (2), (3), интересны тем, что по мере приближения их частоты к циклотронной компонента - электрического поля, вращающаяся в электронную сторону Е-, стремится к нулю. Действительно, считая, как и выше, что выполняется условие |еш|>1, из (1) находим
А ш.—ш
Е-^-~-Ае-^Е^ —--------------- Ае‘*'Ех, (4)
2 Га ю
Где А= — ^ В(1——/?[58]). Правое равенство в (4) справедливо при прене -
Брежении эффектами теплового движения электронов, когда с
2 со—(о.
Из (4) следует, что при Т,=О электронная компонента плазмы не поглощает энергию электромагнитных колебаний, даже если частота последних равна циклотронной. Этот результат можно получить непосредственно из выражения для количества энергии, поглощаемого электронами в единице объема в единицу времени:
Лг= Ие (Е}') = (йе о I £. I г+ 4- 1т е„ Ие (Е-Е/) + 1т е„ I£« 12) .
/ С
(5)
Роль теплового движения электронов состоит в том, что за счет эффекта Доплера оно «размывает» циклотронный резонанс на область частот 6й>»ЛХ!7,. В этой области величина О остается конечной, поэтому Е~ не обращается в нуль. Несложные оценки показывают, что при сО—(йв~кгив два последних слагаемых в (5) имеют тот же порядок величины, что и первое,
А —|£’1|2. Таким образом, мы приходим к выводу о том, что резо -
8я
Нансное циклотронное взаимодействие всецело обусловлено эффектами теплового движения электронов. Этот вывод не относится к колебаниям, распространяющимся вдоль магнитного поля (0=0). Действительно, в этом случае показатель преломления одной из двух ветвей колебаний обращается в бесконечность (см. (2)). Для таких колебаний использованная выше схема решения системы (1), основанная на разложении по малому параметру 1/е(1), становится непригодной. Однако в интересующем нас случае неоднородного магнитного поля с У#<ДН0 практически невозможно возбудить колебания, для которых при приближении к резонансной точке выполнялись бы условия: 0-^0, и-*«».
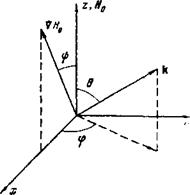
Действительно, вдали от резонансной точки показатель преломления является конечным (гс~1), а неоднородность магнитного поля изменяет лишь ту его компоненту, которая параллельна УЯ0. Поэтому в окрестности резонансной точки по крайней мере одно из двух условий 0~^О, л-*-«» не может быть выполнено. В то же время именно колебания с 0-^0, П-*00 Представляют наибольший интерес, если УЯ01:Н0 (см. [1 ], а также введение).
Го поля. Оценим то расстояние, на котором электрон выходит из фазы с колебаниями. Для этого подсчитаем разность фаз как функцию расстояния вдоль УЯ0:
1 * ^2
Ф(«) =----------- - Г (<1)'-<й.(*))<2«=—------------- (6>
УхСОв^*' 2£1>гСОЗ|)
Здесь о)/=о)—KtVi’, разность фаз отсчитывается от резонансной точки, где (O'=(Oe(S).
Из (6) следует, что размер зоны, в которой отдельный электрон резонансно взаимодействует с колебаниями, по порядку величины равен As~ «(Lpe cos t|?)4L. Электрон проходит ее за время Af«(l/o)) (L/Pe cos - ф)v*. Очевидно, что расфазировку, вызываемую движением электронов вдоль неоднородного магнитного. поля, необходимо учитывать лишь, если характерное время сбоя фазы из-за неизбежных в реальных условиях случайных воздействий значительно превосходит At. К сбою фазы могут приводить немонохроматичность электромагнитных колебаний и кулоновские соударения.
Первый фактор дает характерное время сбоя Д£,»1/Ай), где До> — ширина спектра колебании, второй — Д*2« (A/Kz2Vzz)'!IY где v — частота куло - новских соударений (см., например, [10]). Магнитное поле будем называть слабонеоднородным, если &T<*>L4T значительно превосходит min (А*ь Д*2). Если это условие выполняется, то из-за быстрого сбоя фазы электрон «чувствует» лишь локальное значение магнитного поля. Поэтому при описании резонансного циклотронного взаимодействия можно воспользоваться выражениями, полученными для случая однородного магнитного поля, считая в них величину Но медленно меняющимся параметром. Именно такой подход использовался в работах [""*].
Отметим, что кинетическое рассмотрение оправдано лишь, если выполняется условие min(AЈi; Att) ^>(кгив)~1. Оно означает, что разброс в положении резонансных точек для электронов с различными значениями 17ж, вызванный эффектом Доплера (As'^Lk^JiО) значительно превышает размытие резонансной зоны, обязанное случайным воздействиям (AS" ^ /1 1
«minL/o)(------------ ;------ ). В обратном случае для тензора диэлектрической
Д*1 Д*2 /
Проницаемости можно использовать выражение, полученное в гидродинамическом приближении, введя в резонансные знаменатели малую мнимую добавку 1/(о)—o)e(s))”** 1/(о)—со«(s) +iv/), где v'=mдx(l/Af,; 1/Af2).
Б. Коэффициент поглощения. Предположим, что вдали от резонансной зоны возбуждается монохроматическая электромагнитная волна. Неоднородность магнитного поля приводит к тому, что компонента волнового вектора колебаний вдоль Vtf0 становится функцией координаты S. В результате в ква3|иклассическ0м приближении выражение для электрического поля колебаний принимает вид
Е(г. T) «Е0Exp ^ — Mt+ik'r+i Jk,(s)dr J,
Где ka=(Jte.)e«, k'—k—k„ e,=V//0/|Vtf0|.
Коэффициент поглощения колебаний можно найти, сопоставив амплитуду колебаний по разные стороны от резонансной зоны. Нетрудно видеть, что коэффициент поглощения (по мощности) дается следующим выражением:
F KtVe
TOC o "1-5" h z Где Г= 1 Cfs Im Л*. Здесь, считая размер резонансной зоны As'«-—-—L J ш
В которой происходит поглощение колебании, малым по сравнению с размером плазмы, мы расширили интервал интегрирования до бесконечности. Выражение для Im К$ находим из (3) (см., например, [5]):
Ык-ЧжУ*,Ш- <8>
Здесь через At обозначено второе слагаемое в (3). Учитывая вид А0 (см.
(2) ), для ДАо/дк, удобно использовать следующее представление:
!Г=2*-77РГ+2(М<) яТГм • (9)
Дк. д{к2) дк±г)
То же самое выражение для коэффициента поглощения можно получить, рассмотрев движение волнового пакета. При прохождении через резонансную зону амплитуда волнового пакета уменьшается на множитель
Оо
Схр(-Г'), где Г'= F 4(S(T))Dt. Используя соотношения lf(s) =
— оо
Д /^Ао"‘ / 1 , Ds Did ДА0 / ДЛ* ~1
1 ( дш ) 6 ( O{S) )’ “ F/p ’ ‘*~~Dk~A Дк. ( Ды ) ’
Получаем, что Г'=Г.
Следует отметить, что если 0->-л/2, то при вычислении Vtrp нарушаются условия применимости метода последовательных приближений по малому параметру Ktve/(Ny используемого в настоящей работе, при этом выражение для Vzrp становится комплексным (см. [9]). Однако при |?=л/2, т. е. например, для геометрии магнитного поля токамаков, вычисление F. rp не сопряжено с какими-либо трудностями.
Выражение для Im/c* зависит от координаты S лишь через аргумент функции
ИГ(Ш) =Е— (l+ fe*w ,
TOC o "1-5" h z ' Ini '
Где W=(I)S/2!IKzve. Интеграл, входящий в Г, вычисляем, вводя новую переменную интегрирования S->~W [u]:
/= f Dw Re-~— = — Imlimln ( — + F Dw'E"'1} = л*. (10)
J W{W) 2 ^0» 2I J /-»2
- 30 о
Используя формулы (2), (8) — (10), окончательно получаем следующее выражение для величины Г, определяющей коэффициент поглощения Г) (см. (7)):
Г= (±.МвА*п.*(1|.+2,_1)»(ИАЧ-д-1)-‘В-‘, (11)
4 С с / Qn
Где В= (n±z+n2+2q—3) sin 0 cos ср sin (n±2—G+2) cos 0 cos J>.
В. Правило обхода Ландау. Отметим, что интеграл (10) может быть вычислен и иным способом. Функция W(W) является аналитической, поэтому коптур интегрирования можно сместить в верхнюю полуплоскость переменного W так, чтобы он обходил начало координат на расстоянии
|ш|»1. В этой области для W справедливо асимптотическое представление:
(L+-^RV
Zi W 2Wl /
Подставим это выражение в (10) и разложим знаменатель подынтегрального выражения в ряд по 1 /2ш2, учитывая лишь два первых члена разложения. Правильный результат в (10) можно получить, используя извест - 1
Ное соотношение Im — =—лб(ш), которое эквивалентно правилу обхода W
Ландау. Второе слагаемое в асимптотике W учитывает эффекты, вызываемые давлением электронов, которые можно учесть в гидродинамическом приближении. Разумеется, в резонансной зоне, где собственно и происходит поглощение колебаний, гидродинамическое приближение неприменимо. (Выражения для компонент тензора диэлектрической проницаемости, Полученные в гидродинамическом приближении, имеют особенность в точке циклотронного резонанса.) Тем не менее мы получаем правильное значение коэффициента поглощения, если для продолжения решения через резонансную зону воспользуемся правилом обхода Ландау. Ниже мы покажем, что такое упрощенное описание дает правильный результат и в случае сильнонеоднородного магнитного поля. Возможность использования упрощенного описания при V#0||H0 Была обоснована в [4*12].
3. Сильнонеоднородное магнитное поле
А. Интегральное уравнение. В соответствии с классификацией, проведенной в разделе 2а, магнитное поле считается сильнонеоднородным, если на резонансное циклотронное взаимодействие существенно влияет расфазировка, вызываемая движением электронов вдоль неоднородного магнитного поля. Электроны, двигаясь вдоль поля, «переносят информацию» об электрическом поле волны. В результате отклик плазмы становится нелокальным и соответственно волновое уравнение — интегральным.
При выводе волнового уравнения воспользуемся методом последовательных приближений. Поскольку в окрестности резонансной точки выполняется соотношение |Ј-|< |£+|, |£*| (см. выше), в первом приближении положим £'_=0, Ti= 0. При этом для определения характеристик колебаний по-прежнему имеем уравнение (2). В следующем приближении, считая Е+ и Et Заданными, находим Е_ из аналога верхнего уравнения системы
1 TOC o "1-5" h z 4лI
— N±zE+e-2i'+nJLnlEte-i' +—j-=0. (12)
2 to
Предположение о постоянстве амплитуд Е+ и Ег законно, если Я«2Г<1. Поскольку величина Г пропорциональна малому параметру Vjc)Z, то это предположение в реальных условиях часто оправдывается.
При учете теплового движения электронов для /_ получаем следующее выражение:
, - « (13>
/- (s)*8 F Dvj0(Vt) F Dt, (£_(5(Л)) + -±^£2е-,Л ехр(гФ(f, f,)).
4л J J tOi /
В выражениях (12), (13) из возмущенных величин выделен множитель exp(i(kr—(At)). Так, например, /_fr, T) =/_(s)exp(i(kr—At)); T=t(s) = = (s—S(0) )/vt cosij?;
И
Ф(*»Ft)®8 JDt2b)e(s(t1)) + (ktut—tii) (t{—t) = T
— (<ns/L+ktvt) (tl—t)+(a)Vt/2L)cos t|?(*i—*)2;
Функция распределения электронов по скоростям предполагается равновесной — максвелловской. При выводе (13) в силу условия /ср,<1 учтены лишь члены первого порядка малости по К±и±/(ов. В выражении (13) усреднение по!;х уже произведено. Отметим, что в (12) опущены слагаемые вида Это, как следует из проведенного ниже рассмотрения, спра
Ведливо при выполнении довольно «мягкого» неравенства (ре/£):/:(с/17е)2<1.
![]() Представим искомую функцию £-($) в виде
Представим искомую функцию £-($) в виде
(14)
Здесь £=5/'А5, Д$=(£ресо8 ф)7’, /(£) — неизвестная функция, посредством которой учитываются эффекты, вызванные тепловым движением электронов вдоль магнитного поля. В гидродинамическом приближении /(£)=0Г и (14) переходите (4).
|
0 — оо Ов + |ехр ( - ^ (£,2-£г) ) } = о, С |
 Выражая Е+ из нижнего уравнения системы (1), взятого в гидродинамическом приближении, а также используя (13) и (14), приводим уравнение (12) к виду:
Выражая Е+ из нижнего уравнения системы (1), взятого в гидродинамическом приближении, а также используя (13) и (14), приводим уравнение (12) к виду:
|
|
|
Оо |
|
О |
(15)
|
О о О |
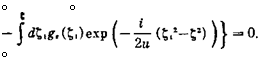 Б. Решение интегрального уравнения. Интегральное уравнение (15) является сингулярным уравнением Фредгольма первого рода с бесконечными пределами интегрирования. Обычно такие уравнения решают методом интегрального преобразования Фурье. Однако этот метод полезно использовать лишь, если ядро интегрального уравнения является ядром смещения, т. е. функцией от разности £1—£. Поскольку в данном случае ядро зависит от сочетания £12—£ то уравнение для фурье-образа оказывается не проще исходного, и поэтому получить решение таким методом не удается. Однако для определения коэффициента поглощения нам достаточно знать лишь четную часть функции #(£), вычисление которой оказывается более простым. Эта часть #.(£) удовлетворяет следующему уравнению:
Б. Решение интегрального уравнения. Интегральное уравнение (15) является сингулярным уравнением Фредгольма первого рода с бесконечными пределами интегрирования. Обычно такие уравнения решают методом интегрального преобразования Фурье. Однако этот метод полезно использовать лишь, если ядро интегрального уравнения является ядром смещения, т. е. функцией от разности £1—£. Поскольку в данном случае ядро зависит от сочетания £12—£ то уравнение для фурье-образа оказывается не проще исходного, и поэтому получить решение таким методом не удается. Однако для определения коэффициента поглощения нам достаточно знать лишь четную часть функции #(£), вычисление которой оказывается более простым. Эта часть #.(£) удовлетворяет следующему уравнению:
|
|
(16}
В силу четности функции £е(£) достаточно решить уравнение (16) для £>0. Введем новую переменную |=£2. Такая замена приводит уравнение
(16) к виду, удобному для использования метода интегрального преобразования Лапласа. В результате применения преобразования Лапласа получим:
|
Л ¥ |
|
Ехр |
|
(-ж)' |
|
||
|
||
|
||
Здесь G{P) = J DV(g)Exp(—/?£) — изображение по Лапласу функции
С помощью обратного преобразования Лапласа искомая функция представляется в виде
|
Й/7 7 |
|
І |
|
-1 2pJ |
|
4р / L W(i/2p) 2р |
|
Т = аГ (*‘-Т)1ехр(~гх‘е) 0ехр (17) [ |
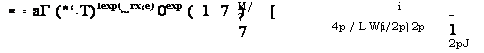 |
(18)
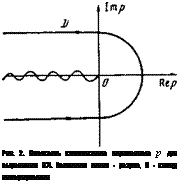
Здесь интегрирование проводится по контуру Д изображенному на рис. 2.
Интеграл, входящий в (18), легко вычисляется как при малых, так и при больших значениях В первом случае он определяется областью, где |р|>1, и соответственно У(У2р)^. Если выполняется условие |£|<
|
Рис. 2. Плоскость комплексного переменного Р для выражения (17). Волнистая линия - разрез, Л - контур интегрирования |
 <тах(1; х*), то из (18) получаем
<тах(1; х*), то из (18) получаем
(19)
/(£) * ~^уі: {*'~~A)Cos (x«Ј)exp(-ix-&) •
При |Ј|>max (1; х,), используя асимптоти -
|
( |
І 2 р
——) ~ —— (1 —
2P/IPKC1 л/і
—2Р1 + ...), находим
/(£)»(*. - ^J-) Cos(х,£) ехр(-Ix,Ј).
5 (20)
Если не рассматривать выделенного случая, когда 1—д—/г2-*-0, а х±/Л-*-«>, то в области £>тах(1; х,) имеет место неравенство |£|^|/(£) |. Иными словами, в этой области для £-(£) справедливо «гидродинамическое» представление (4). Этот результат вполне естествен, поскольку условие
£»тах (1; хх) означает, что мы находимся вне резонансной зоны
5>тах (Дз, Дз') (см. раздел 2а).
В. Коэффициент поглощения. Коэффициент поглощения т] равен отношению энергии, поглощаемой электронами в единицу времени в трубке единичного сечения с образующими, параллельными градиенту магнитного поля, к проекции потока энергии в волне на направление градиента Р,:
Л -1 * Ке<Ь Е‘) - 1 * Ке +у/Х+/Ж ) • (21)
Здесь составляющая тока ]-—]х—ЧУ определяется формулой (13); составляющая /+*=/х-1-1/у=(1(1)г/8л)д£+ не дает вклада в коэффициент поглощения, а для составляющей /, по аналогии с (13) получаем следующее выражение:
TOC o "1-5" h z I 2 К °° L(>) К V
—~ — f Dvtvtf0(vt) f DtxE-(s(t{)) + -^-E1e-iAex])(i<b(tytl)).
ОЛ (0* J J L (De J
—. oo — oo
(22)
Проведя в (21) интегрирование по частям, находим
<Dpi 1 Lpe Г Du f , , , ,
1 41 — е Шг+1-г) +
32л '* Р, ие cos ф J И I
Т о
+2^P, Im[Ј,-exp{i (ф + f-)} (/+/+•-/-/-*)] +
+ (*lP.)2(U+I,+U-I2)IЈ. I2}. (23)
«О
Здесь /*=j dЈЈ-(S)exp(i4M$)),
— оо
Ов
Yt=j dtexp(l, F*(6)), V*{t)-*Jt±V/2u.
— OO
Для обеспечения абсолютной сходимости выражений (21), (22) мы предполагаем, что фазовая корреляция «сбивается» на достаточно больших интервалах времени, которым отвечают. большие расстояния от резонансной точки, Фактически из-за того, что при ISl”»*00 экспо
|
J 2 —-Lml— ) —п±г(пг+2д-1УЕ,\ эР, с I Q |
![]() Нента ехр(±г'Чг±(5)) быстро осциллирует, интегралы по D% определяются окрестностью точки стационарной фазы £*=±ах,‘ размером 6T,^Ult. Причем поскольку характерные значения И По порядку величины равны единице, то во всей области, определяющей значение интеграла по нельзя использовать ни одно из упрощенных выражений (19), (20). Подставляя в (23) /(£) в виде (18) и проводя интегрирование по D% и Dp (см. Приложение), а также по Du (см. (10)), для коэффициента поглощения получаем следующее выражение:
Нента ехр(±г'Чг±(5)) быстро осциллирует, интегралы по D% определяются окрестностью точки стационарной фазы £*=±ах,‘ размером 6T,^Ult. Причем поскольку характерные значения И По порядку величины равны единице, то во всей области, определяющей значение интеграла по нельзя использовать ни одно из упрощенных выражений (19), (20). Подставляя в (23) /(£) в виде (18) и проводя интегрирование по D% и Dp (см. Приложение), а также по Du (см. (10)), для коэффициента поглощения получаем следующее выражение:
_ ... -------------------- (24)
16Р, с / Q
В приближении холодных электронов проекция потока энергии на направление градиента магнитного поля имеет вид (см., например, [2])
±£).В1ЕА (25)
8л П^Пг
Где величина В была определена выше (см. (11)).
Подставляя (25) в (24), убеждаемся, что коэффициент поглощения совпадает с 2Г, что и следовало ожидать при Г<1 (см. (7)). Отметим, что тот же самый результат получается, если при вычислении плотности тока
1, входящей в формулу (21) для т|, использовать приближение слабонеоднородного магнитного поля (см. предыдущий раздел).
4. Выводы
Таким образом, нами проанализировано резонансное циклотронное взаимодействие при различных значениях величины градиента магнитного поля (УЯоЯНо).
Циклотронного резонанса можно характеризовать показателем преломления, полученным для случая однородного магнитного поля, считая величину поля медленно меняющимся параметром. При сильной неоднородности для строгого описания резонансного циклотронного взаимодействия необходимо использовать интегральное уравнение. При этом хотя размер резонансной зоны, в которой происходит обмен энергией между колебаниями и электронами, определяется рядом факторов (эффект Доплера; расфазировка, вызванная движением электронов вдоль неоднородного магнитного поля; сбой фазы из-за внешних случайных воздействий), значение коэффициента поглощения дается единым аналитическим выражением, вне зависимости от степени неоднородности магнитного поля. Наиболее просто это выражение можно получить, если для описания движения ■электронов в колебаниях использовать гидродинамическое приближение, учитывая при этом давление электронного газа. Полученное таким образом волповое уравнение оказывается сингулярным — оно имеет особенность в точке циклотронного. резонанса. Для продолжения решения через эту точку следует использовать правило обхода Ландау.
ПРИЛОЖЕНИЕ
При использовании функции /(£), определяемой соотношением (18), в выражении (23) появляются интегралы вида
TOC o "1-5" h z г4«р(,б*-^Н——^-1. (П.1)
^ 2И) 1р'' 4рД (1/2Р) 2Р
— 00 И
Меняя порядок интегрирования, вычисляем интеграл по
- ехр(-хх2/4р) г я7* я п
£ Ръ{р±У2и) [ У(№р) 2р ^
Подынтегральное выражение в (П.2) имеет полюс первого порядка в точке Р± -- =^1/2И и точку ветвления Р—0. При |р|-*« функция, стоящая под интегралом, убь: вает быстрее 1/|р|, следовательно, в соответствии с леммой Жордана контур 0 можно дополнить дугой радиуса в правой части комплексной плоскости р, причем
Интеграл по этой дуге равен нулю. Тогда интеграл 1± определяется вычетом в точке Р±:
|
(П.3) |
![]() (IXx*U Г Я1'» I
(IXx*U Г Я1'» I
Институт атомной энергии Поступила в редакцию
Им. И. В. Курчатова 5 июня 1979 г.