НЕУСТОЙЧИВОСТЬ ПОЛОЖИТЕЛЬНОГО СТОЛБА В КОРОТКИХ РАЗРЯДНЫХ ТРУБКАХ В ПРОДОЛЬНОМ МАГНИТНОМ ПОЛЕ
А. В. Тимофеев
В работе исследована устойчивость положительного столба газового разряда в короткой разрядной трубке. Показано, что в достаточно короткой трубке первая гармоника (по азимуту) не возбуждается, при дальнейшем укорочении длины трубки положительный столб становится устойчивым по отношению ко всем гармоникам.
Изучая диффузию плазмы из положительного столба газового разряда в продольном магнитном поле, Ленерт[]] обнаружил, что начиная с некоторого Нжр. уход частиц становится аномально большим. Позднее существование критического поля было подтверждено целым рядом авторов^-4]. Ленерт и Ху[2] определили его величину в длинных разрядных трубках (/>100 а; I — длина, а — радиус трубки) для целого ряда газов (N2, Н2, Не, Аг, Кг), Теоретическая интерпретация этого явления была дана Кадомцевым и Недсспасовым [5]. Они показали, что плазма положительного столба при Н^>Нкр. становится неустойчивой по отношению к винтовым возмущениям, и это приводит к увеличению диффузии. Соответствующие расчеты критического магнитного поля хорошо согласуются с экспериментальными результатами. В пользу существования такой неустойчивости свидетельствуют также результаты работы [в], в которой наблюдалось спиралевидное искривление шнура газового разряда, причем в соответствии с[э] сила, действующая на ток
В спирали была направлена наружу.
Однако устойчивость положительного столба в [5] исследовалась в ограниченных условиях: разрядная трубка считалась достаточно длинной, рассматривалась только первая гармоника /п = 1, магнктное поле полагалось не очень сильным (ионы не замагничены). В таких условиях одинаково важную роль играли диффузия электронов вдоль магнитного поля и диффузия поперек его. В соответствии с этим в уравнении непрерывности электронов члены, описывающие продольную и поперечную диффузию, были одного порядка - j - (-') ~ 1. ^2 = --- циклотрон
Ная частота электронов, т — время между столкновениями электрона с молекулами нейтрального газа, те — масса электрона^.
В ['] содержится указание, что в более коротких трубках неустойчивость может начаться с раскачки колебаний с высшими т. Следовательно, представляет интерес снять эти ограничения.
Мы рассмотрим устойчивость положительного столба газового разряда в довольно сильных магнитных полях, когда имеет значение за-
Магниченность ионов, и в коротких трбках при ((Jt) 1, когда пре
Обладает продольная электронная диффузия.
|
» СТ. » С-Ь» Нов; о, =------------- подвижность электронов; Ь< =-------------------- подвижность ионов. /п# /п< Устойчивость колебаний исследуем методом малых возмущений, причем В силу цилиндрической симметрии возмущения /II И?! ищем в виде: /(г) + Здесь о) — частота исследуемых колебаний; к — про Дольное волновое число; 0 — азимутальный угол. Систему уравнений для /I,, срг удобнее составить из уравнения непрерывности ионов и амбиполярного уравнения поперечной диффузии. Последнее получаем, умножая уравнение непрерывности электронов на поперечную подвижность ионов 6*х = : -} > а уравнение непрерывности ионов на попе - |
|
1 - т; Речную подвижность электронов = - и складывая результаты. |
|
Ъ, |
|
Ь. |
|
Если перейти к новым функциям п1г % = ~ п0у1 — |
|
Т2 Г2 |
|
I = |
|
СІГ- |
|
Г СІГ |
|
А = (—/о) — 2)-^ а.- В = к-(Ъ-)Ч |
|
Іт Г |
|
Ф(0,)е> |
|
Здесь Ро = — ; ао — первый корень функции Бесселя нулевого порядка; Т Т. |
|
N0 — плотность при Г— О, В,' |
|
■коэффициент диффузии электро - |
|
ТПш |
|
Дп Ді |
|
Дп |
|
СІІУ (/IV,) = -+- СІІУ (/IV,) = Z/I. |
|
(1) |
|
|||
|
|||
|
|||
|
|
||
|
|||
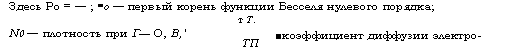 |
|||
|
|||
|
|||
|
|||
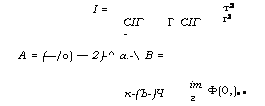 |
|||
Л, = (-/<0-2) ^ -+- Исо0 (2')? /Ть
В, = Л* (2-)2 Й. ч - * (2-) л, ч - ± ^,
* = 1-нр/; р = 1—р/2, т = 1— Р1+рЧ3; 8 = —1-|-р/, е = — 1— *„
А1 = —Р2, р! = —Р— р*+р4г; Т1 ^-р+рЧ-ь-рЧ'—рЧ*, =р-*~р*—р4', н = —1-ь-рч-р1,
4 1 Л*. . . п_1-(ат>!
«0 ' Ь, ' Р (£>Т)2 »
V0 = Ь, Е0 — продольная невозмущенная скорость электронов. Поскольку решение системы уравнений (4) при п0 = ($0г) представляет значи -
Г1
Тельные трудности, МЫ приближенно ПОЛОЖИМ n0 = N0е Ь' . Если ВЫ“' брать 6=^—, то функция Гаусса будет хорошо аппроксимировать -
2г
Реальное распределение. При этом ф = — а А, Аъ В% В становятся постоянными.
Так как в уравнениях имеется оператор Бесселя, то для решения естественно применить интегральное преобразование с ядром 1т(гх}
TOC o "1-5" h z "1 (г) = | V (х) 1„ (гх) с/х. (5>
*1
Для ЭТОГО СВОДИМ систему К одному уравнению ДЛЯ Пх (г)
{-Ь*+(А -+-В,) I—£ I -+- £ А -£г+АВу - А. в] 7.1 (г) = 0. (6>
Применив (5), для и(**) получаем следующее уравнение
** (Л В1 (7)
~£Г х (дг2_+“ А)
Решая последнее, получаем
Ьу
<о(х) = е 4 (л:2-«- А)ах (8)
где
.Л, Я 61. 5 ^ А1В Ь*
А— Л 4 ’ Л 2 1в
Согласно общей теории интегральных представлений [7], пределы интегрирования выбираем такими, чтобы обратить в нуль присоединенную билинейную форму. В нашем случае она имеет вид
•у (х2-*-А) V (х) 1т(гх) (9)
Поэтому МОЖНО ВЗЯТЬ - ЛГ! = О, ДГ2=00.
Таким образом, имеем
00 6*х*
Пх (г) = const [ е 4 (хг-ь-А)* х$Im(rx)dx. (10)
О
В коротких трубках при £6(2т)>1 ^------------- и если---------------- 1, как,
Например, в [*» 2’ °], то А - р - и
6V
Ni (г) ^ const J е 4 x4m(rx)dx =
=<—-5-ЧйЙг1 |(т)Т
Т=-^-(Р —"1 —1).
Так как подынтегральные выражения в (10), (11) существенно различаются только в той области, где за счет обрезания экспонентов они становятся достаточно малыми, собственные значения <*> находим из условия П!(а) = 0. Формально это условие справедливо только при учете диффузии поперек поля, так как в противном случае на границе возможен скачок плотности. Однако если не рассматривать колебания, существенно связанные с границей, и ограничиться возмущениями, развивающимися во внутренней области положительного столба, то в качестве приближенного граничного условия можно принять Пх(а) = 0- Получающееся дисперсионное уравнение имеет вид
А=Т^Г (12>
I m
ИЛИ
(—До — Z) [кгЬ2 (2х)2 tp (1 н-/)-*-2Сш (1 ч-pt) — 2/m (2т) t (—1 - t-p)] -4-
-i - Ik«,[к*Ьг (Q-f tp (1 -/)-+-2Cm (1 - pf-)-+-2/m (2x) t (-1 — p/)]-+- -+- k2D. [№ (2x)2 Pp 2C„ (1 - p/-HpV) -
— 2/m(Qx)/(—l-t-p/-i-pV)] = 0. (13)
Здесь *1 = ^ (2f - ь-ш-1-2), Cm = b'1(*?n—, определяется корнями
Вырожденной гипергеометрической функции. В (12) хт является эффективным поперечным волновым числом. Вырожденная гипергеометриче - ская функция протабулирована лишь для низших т до т = 3 [л]. Однако при больших т для интегрирования (11) можно применить метод перевала с точностью, возрастающей при увеличении т. Приближенное дисперсионное уравнение в этом случае получаем из условия
NI (а) = const V2 (р —1)| =0.
|
Обратным степеням - 1 — . Дисперсионное |
![]() Здесь const 1т |-j - V2(p —1)|—первый член асимптотического ряда по
Здесь const 1т |-j - V2(p —1)|—первый член асимптотического ряда по
Дисперсионное уравнение совпадает
ПО форме С (12), (13), С - р - , где ат — первый корень функции
Бесселя с индексом т. При т^>1, что соответствует большим поперечным волновым числам, естественно искать решение в квазикласси - ческом приближении /(г) — е*Кг. Тогда дисперсионное уравнение принимает вид
TOC o "1-5" h z
|
(14) |
![]()
|
А = |
![]() АВ <) <> _ ш - <)
АВ <) <> _ ш - <)
!— ----- х2 ; X2 = —- х2.
Д. ч-х! ,я' т г2
Появление добавочного члена х^ по сравнению с (12) связано с тем, что ранее решение находилось при условии к~Ь~ (2-)2^> 1, что эквивалентно предположению о малости поперечной электронной диффузии
|
(2-ї2 1 |
![]()
|
X - - |
![]() , а это, очевидно, выполнено только для первых гармоник а = 1.6 Ь.
, а это, очевидно, выполнено только для первых гармоник а = 1.6 Ь.
При малых т из (13) получаем
2у0Ь (2т) і
КЮ‘ ~~П7 ПьГ т (2т)2 ір 2Ст1
Іш («>) =
4т -
(«х)*
|
КгРг Гк*ь* №)* 'У - кЧ1 (<2*г - Гр2Ст ч- 4 (С-т - т2)1 [*242 (2-)2 (р _ 2С, л]2 - н -^т |
|
Неустойчивость наступает при 1т (о>) = 0. Ограничимся для простоты В нуль при //кр. =//0(1 ± 1 —О Ы __ с * 2Ст (Ш4 /7р-- » ГП. I --------- ■ |
|
(**)■■>’ ___ ~ д. |
|
Здесь меньший корень дает значе- Качка колебаний с определенным т, второе же значение Нкр. согтвет- Ствует моменту стабилизации данной гармоники. Если £1 = -^^->1> То первая гармоника всегда устойчива, и неустойчивость может начаться ОI Ние , как видно из приведенной ниже таблицы, монотонно убывая, Стремится приблизительно к 0.5, то при (кЬ)4 ]> положительный В [’'] было обнаружено, что в газовом разряде, начиная с некото- |
|
ГІ+-2 » |
|
|
(16) |
|
V |
|
|
 |
В положительном столбе были такими, что можно было считать kb (2~)^Т. С нашей точки зрения появление шумов обязано неустойчивости одной из первых гармоник. Значение //кр. ~ 1000 гс по порядку величины согласуется с подсчитанным из (16). В рамках линейной теории, не учитывающей воздействия колебаний на нулевой фон, возможна одновременная неустойчивость нескольких гармоник. Возможно, что началом раскачки или стабилизацией какой-то гармоники объясняются скачки в величине шумов. Амплитуда шумов может меняться также и потому, что возрастание эффективной диффузии, вызванное неустойчивостью мелкомасштабных колебаний с высшими /п, уменьшает амплитуду низших гармоник.
В заключение я хотел бы выразить глубокую благодарность Б. Б. Кадомцеву, под руководством которого была выполнена эта работа, а также А. В. Недоспасову за полезные обсуждения.