ТОНКОПЛЕНОЧНЫЕ. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ. НА ОСНОВЕ КРЕМНИЯ

Транспорт носителей заряда

В соответствии с моделью распределения энергетических состояний Мотта — Дэвиса — Стрита возможны три механизма переноса носителей заряда в неупорядоченных полупроводниках [25]-[30], [37]-[39].

Если уровень Ферми находится в зоне локализованных состояний N(Ef), то при низких температурах возможен прыжковый механизм прово­димости по состояниям, расположенным вблизи уровня Ферми. При этом

54

носители туннелируют между узлами, слабо различающимися по энергии, на расстояние переменной длины. Данный механизм проводимости полу­чил название прыжковой проводимости с переменной длиной прыжка. Моттом было выведено выражение для этого режима проводимости:

где 70 = const.

Предэкспоненциальный множитель A определяется как

A = і е2 R 2Уф N (Ef).

где R — длина прыжка; Уф — фононная частота порядка 1013 • с-1.

Таким образом, из выражений (3.1) и (3.2) следует, что из зависимости lga ~ (1/T)1/4 при низких температурах может быть определена плотность состояний на уровне Ферми N(Ef). Зависимость Т-1/4 наблюдается в чистом а-Si либо в сильнолегированных образцах гидрогенизированного аморфного кремния, когда плотность состояний вблизи уровня Ферми велика и осуще­ствляется с первым механизмом переноса.

При более высоких температурах носители заряда могут быть либо захвачены на локализованные состояния хвостов валентной зоны и зоны проводимости, либо оказаться в распространенных состояниях зон выше порога подвижности.

Второй механизм проводимости при высоких температурах связан с переносом носителей заряда по локализованным состояниям на хвостах зон. В этом случае подвижность носителей заряда может быть определена из выражения

где exp[-WkT] — больцмановский фактор; W — разность энергий в со­стоянии до и после прыжка или энергия активации прыжка; exp(-2aR) — множитель, зависящий от перекрытия волновых функций; R — расстояние, покрываемое за один прыжок, при энергиях, близких к Ес, перекрытие

большое и exp(-2aR) ~ 1.

Как видим, в выражение для подвижности носителей заряда входит экспоненциальный множитель, связанный с энергией активации прыжка, что обусловливает экспоненциальную зависимость дрейфовой подвижно­сти от температуры. В этом случае в энергию активации электропроводно­сти входит сумма энергий активации концентрации и дрейфовой подвиж­ности. Если перенос заряда осуществляется по локализованным состояни­ям хвоста зоны проводимости, то выражение для а примет вид

а = ад exp(- (Еа - Ер + W)/kT),

где Еа — край хвоста зоны проводимости.

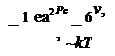Третий механизм реализуется, когда перенос заряда осуществляется по делокализованным состояниям, а длина свободного пробега меньше меж­атомного расстояния, но сравнима с ним (L ~ а), проводимость может быть описана диффузионным движением. В этом режиме подвижность электро­нов определяется по формуле

где а — межатомное расстояние; v — частота прыжков.

Величина рс = 1 - 10 см2/(В-с).

Учитывая, что рс ~ 1/kT, выражение для электропроводности преобра­зуется как

а = ам exp[-(Ec - Ер)/Щ, (3.4)

где ам — минимальная металлическая проводимость.

Она определяется как минимальная безактивационная проводимость. Для большинства неупорядоченных полупроводников величина ам лежит в пределах 10-103 Ом-1-см-1.

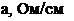
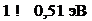
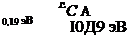
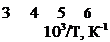
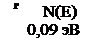10-10 10-12-1!

10-14 10-16

4 5 6 7 8

103/T, К-1

а б

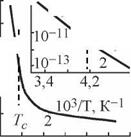
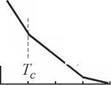
Рис. 3.6. Температурная зависимость дрейфовой подвижности электронов
Pd (а) и проводимости а (б) для пленки кремния, осажденной
в тлеющем разряде при 500 К

Из выражений (3.3) и (3.4) следует, что при переносе носителей заряда по распространенным состояниям валентной зоны и зоны проводимости подвиж­ность слабо зависит от температуры. Энергия активации проводимости опре­деляется энергией активации концентрации свободных носителей заряда.

Измерения дрейфовой подвижности электронов в образце [30], осаж­денном в тлеющем разряде при T = 500 К, показали, что кривая темпера­турной зависимости имеет излом при температуре Tc (~ 250 К), выше кото­рой энергия активации составляет 0,19 эВ, а ниже — 0,09 эВ (рис. 3.6, а). На кривой температурной зависимости проводимости (рис. 3.6, б) также изменяется наклон при той же температуре (~ 250 К). Полученные зависи­мости можно объяснить переносом по нелокализованным состояниям при T > Тс, причем энергия активации дрейфовой подвижности обусловлена за­хватом носителей в область мелких локализованных состояний у края зоны проводимости, а также прыжковым механизмом переноса по этим состоя­ниям при T < Тс.