ТЕОРИЯ сварочных процессов

Термический цикл при однопроходной сварке. Максимальные температуры

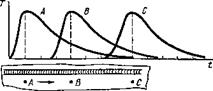
В процессе однопроходной сварки источник теплоты пере­мещается в теле и вместе с ним перемещается температурное поле. Температуры точек тела непрерывно изменяются (рис. 7.6). Вначале температура повышается, достигает максимального зна­чения, а затем снижается. Изменение температуры во времени в данной точке тела называется термическим циклом.

При установившемся температурном поле термические цик­лы точек, расположенных на одинаковом расстоянии от оси движения источника теплоты, одинаковы, но смещены во вре­мени.

Термические циклы точек, расположенных на различных рас­стояниях от оси движения источника теплоты, различаются меж­ду собой. В более удаленных точках температура повышается медленнее и позже достигает максимального значения.

Восходящая ветвь температурной кривой называется стадией нагрева, нисходящая — стадией остывания.

Основные характеристики термического цикла следующие: максимальная температура, скорость нагрева и скорость охлаж­дения при различных температурах, а также длительность пребывания материала выше заданной температуры. Эти харак­теристики цикла зависят от режима сварки, теплофизических свойств материала, конфигурации тела, условий его охлажде­ния, температуры предварительного подогрева.

Максимальные темпера­туры, достигаемые отдель­ными точками, определяются достаточно просто, если из­вестно температурное поле.

В точке максимальной тем­пературы первая производ­ная по времени ИЛИ по рас - рис 7 6 Изменение температуры в точках стоянию равна нулю: тела А, В, С со временем

Производная по времени или по расстоянию берется в за­висимости от того, какую координату содержит выражение для температурного поля. Время t и координата х, как известно, связаны между собой скоростью сварки.

Аналитическое определение максимальной температуры в массивном теле и в пластине, если за исходные брать форму­лы (6.22) и (6.26), сопряжено с трудностями. Максимальную температуру аналитически выразить не удается. Возможно чис­ленное определение максимальной температуры, которое по су­ществу состоит в построении участка термического цикла. Если необходимо определить максимальную температуру в точке, на­ходящейся на расстоянии уо от оси движения источника теплоты, то задаются несколькими отрицательными значениями х0, под­ставляют х0 и уо в формулы (6.22) и (6.26), находят приращение температуры и строят график термического цикла в зависимости от Хо. Координату Zo в уравнении (6.22) полагают равной нулю.

Другой путь определения максимальной температуры состоит в использовании номограмм, приведенных на рис. 7.5, а, б. Вы­числяют значение vl/(2a), где 1=уо, находят величину параметра на вертикальной оси, а затем определяют максимальную темпе­ратуру Ттах = ATi-{-TH. Необходимо иметь в виду, что кривая на рис. 7.5, б вычислена по формуле (6.26) без учета теплоотдачи, т. е. при 6 = 0.

Наконец, возможно определение максимальной температуры в предположении, что источник нагрева быстродвижущийся. Для точечного источника теплоты на поверхности массивного тела путем использования формул (6.46) и (7.10) получаем

где ro = yo + zo.

Для линейного источника теплоты в пластине из формул (6.47) и (7.10) находим

(7.12)

где уо — расстояние от данной точки до оси шва.

При сварке в условиях нормальной температуры, хотя подо­грев как таковой и отсутствует, 7^ «290...300 К.

Пример 3. Автоматический аргонно-дуговой сваркой соединяют встык одно­проходным швом листы 6 = 6 мм из сплава АМГ6. Режим сварки: / = 400 A. U = = 16 В, 11 = 0,5. Скорость сварки v= 18 м/ч = 0,5 см/с.

Определить максимальную температуру, которая достигается на расстоянии /={/= 4 см от оси шва при ГН = 300 К.

Теплофизические коэффициенты находим из табл. 5.1: Я, = 2,7 Вт/(см-К); а= 1 см2/с; ср = 2,7 Дж/(см3-К).

Теплоотдачей в воздух пренебрегаем. Определяем эффективную мощность источника теплоты: <7 = л W = 0,5-16-400= 3200 Вт. Максимальную температуру определяем по номограмме, приведенной на рис. 7.5, б. Вычисляем безразмер­ный критерий:

ol/{2a) =0,5 -4/(2- 1)= 1.

По значению vl/(2a)= 1 находим

А72лХб/?= 1,1; АТ = 346 К; 7тах= Т„ + АТ = 300 + 346 = 646 К.