Размер зоны нагрева
|
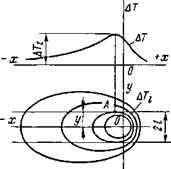
Рис. 7.4. Схема определения ширины 21 зоны, приращение температуры в которой превосходило Д Ті |
Для оценки термического влияния на свариваемый металл бывает необходимо определить ширину 21 зоны, приращение температуры которой выше заданного Д Ті (рис. 7.4). В общем случае ширина зоны нагрева выше ДТі, равная 21, будет найдена, если определить координату у точки А. Точка А, во - первых, находится на изотерме и, следовательно, ДТ = ДГ/, во-вторых, в точке А достигается максимальное приращение температуры на расстоянии у = I, т. е. дТ/дх= 0.
Таким образом, для определения ширины зоны необходимо решить систему двух уравнений. Покажем это на примере наплавки валика на массивное тели.
Из уравнения (6.22) находим:
TOC o "1-5" h z £ = - ■dF'-,-/MII-+"[ f+ ■£(* + Л)] = 0. (7.3)
Полагая 2 = 0 и учитывая, что /2 = у2 = Я2 — х2, из уравнений (7.2) и (7.3) выведем два уравнения в параметрической форме:
i-±T^VT + 25; (7.4)
АІі.:ЛлХа — J_g-P3/(i+p,) (7 5)
qv pi
где рз = vR/(2a).
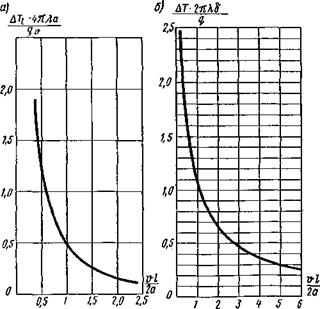
Задаваясь различными значениями р3, находим значения vl/(2a), соответствующие различным приращениям ЛГ;. На рис. 7.5, а представлена номограмма для определения ширины зоны термического влияния при нагреве полубесконечного тела точечным источником. Зная режим сварки, находим вначале значение параметра, отложенного по вертикальной оси, а затем vl/(2a).
Для мощного быстродвижущегося точечного источника теплоты на поверхности полубесконечного тела, используя уравне-
|
Рис. 7.5. Номограммы для определения ширины зоны нагрева 21 движущимся источником теплоты |
ниє (6.42), определим ширину зоны термического влияния аналогичным образом:
2/=У • (7.6)
* nevcp&Ti
Ширина зоны нагрева при сварке пластины определяется так же, как для полубесконечного тела. Уравнения в параметрической форме, получаемые из (6.26) при 6 = 0, позволяют опре
делить ширину зоны нагрева 21:
ir=±P’V4<77»
= e-Vpi-[»'A2«)]‘/f0(o2), (7.8)
Л7/2я>.6
где р2 = vr/(2a).
На рис. 7.5, б показана номограмма для определения ширины зоны нагрева при сварке пластины линейным источником в случае 6 = 0.
Для мощного быстродвижущегося линейного источника теплоты в пластине ширина зоны термического влияния определяется с использованием уравнения (6.45) при 6 = 0 по формуле
Г
2/ =----- -2р. (7.9)
цсрбДГг
Пример 1. На поверхность массивного тела наплавляют валик Определить ширину зоны, нагревавшейся выше температуры Т = 900 К, при которой углеродистая сталь в значительной степени теряет упругие свойства. Режим сварки: эффективная мощность источника теплоты q = 6 кВт, о = 9 м/ч = 0,25 см/с. Теплофизические коэффициенты: а = 0,08 см2/с, Я = 0,39 Вт/(см-К); ср = = 4,9 Дж/(см3-К). Начальная температура тела Тя — 300 К, приращение Т = Т - 600 К.
Определим ширину зоны двумя способами: по номограмме (см. рис. 7.5, а), пригодной для источников теплоты, движущихся с любой скоростью, и по формуле (7.6) для быстродвижущегося источника теплоты.
Определяем безразмерный критерий приращения температуры:
Ь. Т-Алка 600-4-3,14-0,39-0,08
qv ~ 6000-0,25 — ’ '
По номограмме рис. 7.5, а находим vl/{2a) — 2,0.
Ширина зоны, нагревавшейся выше 900 К,
21 = 2-2,0-2а/о = 2-2,0-(2-0,08)/0,25 = 2,56 см.
Определяем ширину зоны по формуле (7.6)
21 =У ТЩДг,718-0,25-4,9-600 = ~/ 7-65 = 2-76 см-
Ошибка в определении ширины зоны составляет около 8%.
Пример 2. Листы из низколегированной закаленной стали 6 = 8 см сваривают за один проход дуговой сваркой при токе/ = 300 А, напряжении дуги (J=34 В и скорости v = 18 м/ч = 0,5 см/с, т) = 0,8. Определить ширину зоны отпуска, которая находится примерно между изотермами 870 и 1050 К, если Т„ = 270 К. Теплоемкость стали — 5,0 Дж/(см3-К).
Находим эффективную мощность источника теплоты: q = iVI — 0,8-34-300 = 8150 Вт.
Воспользуемся формулой (7.9) для мощных быстродвижущихся источников и определим ширину зоны, где L. T = Т — 7„ = 870 — 270 = 600 К:
8150 У 2/(3,14-2,72)
2,600 ----------- 0,5-5-0,8-600 ' - 3'28 СМ’
и ширину зоны, где Д7 = 1050 — 270 = 780 К'
Ширина зоны отпуска
Д = (2/боо - 2/780)/2 = - (3,28 - 2,52) /2 = 0,38 см.