Распространение теплоты от неподвижных источников
МГНОВЕННЫЙ ТОЧЕЧНЫЙ источник
Приращение температуры в точках бесконечного тела в случае действия мгновенного точечного источника будет выражено следующим уравнением:
АТ= , Q '3/2 е-я,/(4«0, (6.1)
ср(4яШ)3/2 v ’
где ДТ — приращение температуры в рассматриваемой точке с координатами х, у, z; / — время, отсчитываемое с момента введения теплоты; R — -jx2 - f - у2 + z2 — расстояние до рассматриваемой точки от начала координат, где была введена теплота.
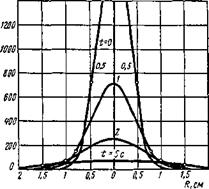
При t=0 во всех точках, где R^= 0, имеем ДГ=0. В точке R=0 при /=0 имеем ДТ —>■ оо. В правильности выбора постоянного множителя в уравнении (6.1) можно убедиться путем вычисления интеграла, выражающего полное количество введенной теплоты во всем объеме бесконечного тела. Это количество в любой момент времени равно Q, так как тело в данном случае не отдает теплоты в окружающее пространство. Распределение температуры при распространении теплоты от мгновенного источника теплоты, приложенного в точке О на поверхности полубес - конечного тела (рис. 6.1), аналогично (6.1) для бесконечного
АТ--
|
|
|
оТ. К |
|
.e-R*/(4at) (6.2) |
|
Плоскость хОу |
|
тела. Это объясняется тем, что граница тела хОу принимается непропускающей теплоту. Так как теплообмен на границе хОу отсутствует и теплота распространяется только в одну сторону от плоскости хОу, то процесс будет выражаться уравнением (6.1) с заменой в нем величины Q величиной 2Q: |
|
2 Q |
ср(4ла1)3/2
|
Рис. 6.1. Распределение приращений температуры по радиусу R в различные моменты времени в процессе распространения теплоты от мгновенного точечного источника в полубескоиечном теле (<? = 2000Дж, ср = 4 Дж/(см3 • К), а = = 0,1 см2/с) |
Теплоотдачей с поверхности хОу можно пренебречь, потому что распределение теплоты в полубеско - нечном теле в основном зависит от распространения ее путем теплопроводности в глубь тела, а не от теплоотдачи. Теплоотдача с поверхности безусловно оказывает некоторое влияние на распределение температуры, но в ряде случаев может не учитываться.
Изотермические поверхности, описываемые уравнениями (6.1) и (6.2), представляют собой сферические поверхности. Убывание температуры по радиусу выражается множителем e~R2^ia‘ в то время как множитель Q/[cp(4nal )3/2] показывает изменение температуры точки R = 0 во времени. Наибольшая температура всегда в точке R = 0.
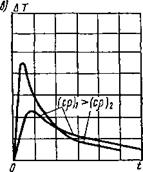
Структура уравнения (6.2) позволяет установить влияние количества введенной теплоты и теплофизических свойств материала на температуру отдельных точек тела. Чем больше Q, тем выше температура точек тела в любой момент времени. Приращение температуры прямо пропорционально количеству введенной теплоты Q (рис. 6.2, а).
Температура точек тела, расположенных на различных расстояниях R от точки О, вначале повышается, достигает максимума, а затем уменьшается (рис. 6.2, б). Чем дальше от места введения теплоты находится точка, тем позже достигается максимальная температура и тем ниже ее значение. С течением времени конечное количество теплоты растекается в неограниченном объеме полубесконечного тела и приращения температуры всех точек стремятся к нулю.
При постоянной теплоемкости ср увеличение коэффициента
|
|
|
6) AT |
|
|
|
R=0 |
т |
|||
|
,1,5 с |
м |
|||
|
^=5 |
|
О! Z 3ft |
Рис. 6.2. Приращения температур от мгновенного точечного источника в полубесконечной теле в зависимости:
а — от количества введенной теплоты Q; б — от расстояния R до точки О, в — от теплоемкости материала ср
теплопроводности металла к приводит к ускорению процесса распространения теплоты. Максимальные достигаемые значения приращений температуры в различных точках остаются теми же самыми, но продолжительность времени с момента введения теплоты до достижения максимальной температуры сокращается во столько раз, во сколько раз повышается теплопроводность материала к. Указанная закономерность обнаруживается, если преобразовать уравнение (6.2), приняв а = к/(ср):
SHAPE * MERGEFORMAT

|
АТ-- |
|
(6.3) |
2Qi/cp —r’c/iai. i)
(4лХ03/2
Коэффициент к входит как сомножитель времени t. Поэтому с увеличением к картина распределения приращения температур в теле остается подобной, но процесс изменения температур ускоряется.
Теплоемкость металла ср при постоянной теплопроводности к оказывает более сложное влияние на процесс распространения теплоты в полубесконечном теле. Изменение теплоемкости можно представить как одновременное действие двух процессов: изменения количества введенной теплоты и изменения скорости распространения теплоты. Запишем уравнение (6.2) иначе:
|
-R7[4«/7p)] |
|
(6.4) |
|
А Т-- |
|
[4иМ/(Ср)]3'2 |
|
2Q/(cp) |
Увеличение теплоемкости ср при к = const равносильно одновременному уменьшению Q и к. Приращение температуры точек тела уменьшается при одновременном замедлении процесса распространения теплоты. На рис. 6.2, в представлены для сравнения термические циклы в одной и той же точке тела при разных ср.
Приращение температуры в пластине от мгновенного линейного источника с равномерным распределением теплоты по толщине при отсутствии теплоотдачи с поверхностей может быть получено путем интегрирования температурных полей (6.1) от мгновенных точечных источников:
|
(6.5) |
cpinat
где r=-jx2--y2 — расстояние до рассматриваемой точки от начала координат, где была введена теплота Q; 6 — толщина пластины.
Температурное поле симметрично относительно оси 2, температура равномерна по толщине.
Влияние Q, X и ср на процесс распространения теплоты и на распределение температур будет таким же, как и в случае мгновенного точечного источника теплоты в полубесконечном теле.
Изменение температуры во времени качественно протекает так же, как и в полубесконечном теле, т. е. температура отдельных точек пластины вначале повышается, достигает максимума, а затем уменьшается. Более удаленные точки нагреваются до меньших максимальных температур. Однако распространение теплоты в. пластине происходит более стесненно, чем в полубесконечном теле. В то время как в полубесконечном теле теплота распространяется в направлении трех координатных осей, х, у, z, в пластине теплота распространяется только в двух направлениях — х и у. Это приводит к тому, что процесс изменения температуры во времени происходит в пластине медленнее.
Теплоотдача через поверхности пластины оказывает более заметное влияние на поле температур, чем в полубесконечном теле. При расчетах температур в пластинах в ряде случаев, в особенности если пластины тонкие, необходимо учитывать теплоотдачу в окружающую среду. Процесс распространения теплоты в пластине с поверхностной теплоотдачей выражается уравнением (6.5), в которое введен сомножитель e~bi (см. п. 5.2):
|
(6.6) |
Д Т _ Q/6 с-г2/(Ш) - Ы
ср(4ла/)
Уравнение (6.6) содержит множитель e~bt, который учитывает теплоотдачу в окружающее пространство, но не отражает того факта, что теплота отдается с поверхности пластины и температура по ее толщине неравномерна. В тонких пластинах, несмотря на значительную теплоотдачу, неравномерность распределения температуры по их толщине незначительна и ею можно пренебречь. В некоторых случаях неравномерность температуры по толщине пластин может достигать нескольких десятков градусов
(см. п. 7.9). Чем продолжительнее процесс распространения теплоты, тем большее значение имеет теплоотдача в изменении температуры пластины.
МГНОВЕННЫЙ ПЛОСКИЙ источник
Приращение температуры от мгновенного плоского источника Q2=Q/F в стержне без теплоотдачи выражается уравнением
AT = --QLF e-*V(4aP (67)
cp(4naf)1/2
Приращение температуры зависит только от координаты х в направлении вдоль стержня и времени t.
Теплота от мгновенного плоского источника в стержне распространяется в основном в направлении вдоль стержня. Если пренебречь теплоотдачей боковых поверхностей, то температуру по поперечному сечению стержня можно считать равномерной, а процесс распространения теплоты — линейным. В случае заметной теплоотдачи с поверхности температура по поперечному сечению стержня будет неравномерной. Теплоотдачу учитывают путем введения в уравнение (6.7) сомножителя е, который отражает лишь понижение средней температуры в сечении, но не выражает неравномерности температуры по толщине стержня:
АТ = —Ш—е-*3^-ь‘. (6.8)
ер(4ясЦ)1/2
Здесь 6, так же как и для пластины, представляет собой коэффициент температуроотдачи для стержня:
b = ap/(cpF),
где р — периметр поперечного сечення стержня, см.
Тепловой поток в воздух в единицу времени с единицы длины стержня в случае одинаковой начальной температуры стержня Ти и среды Гс равен q—apAT. Тепловой поток в стержне еще более стеснен по сравнению с пластиной и массивным телом, поэтому процесс изменения температуры во времени происходит еще медленнее, чем в пластине.
НЕПРЕРЫВНО ДЕЙСТВУЮЩИЕ НЕПОДВИЖНЫЕ ИСТОЧНИКИ
Процесс нагрева тела непрерывно действующим неподвижным источником теплоты можно представить как серию действующих друг за другом мгновенных источников теплоты. Используя принцип наложения, можно найти распределение температур в случае непрерывно действующего источника теплоты путем интегрирования температурных полей от отдельных источников.
|
|
|
-«7(440, (6.10) замену |
|
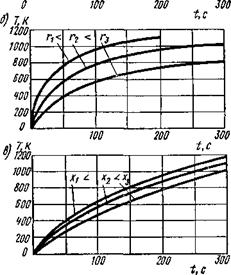
Рис. 6.3. Изменение температуры во времени при действии неподвижного источника теплоты [ {У = 25 В; / = 100 А; г = 0,6; Д = = 0,38 Вт/(см-К); ср = 4,8 Дж/(см3* К)] в точках на расстояних 0,7, 1 и 1,5 см от источника: |
|
2qdt |
|
ср(4ла1)3/2 |
|
Вводим R2/(at)= "2 ем дг=—-— 2лХ/? где Ф(и)=—e~uldu. ■уло Из выражения (6.11) следует, что при t = const приращение температуры убывает с увеличением расстояния R несколько быстрее, чем 1 /R, так как и также уменьшается с ростом R. На рис. 6.3, а показано нарастание температуры отдельных точек во времени. В точках, расположенных ближе к источнику теплоты, предельная температура достигается быстрее. Пример 1. На поверхности массивного тела из низкоуглеродистой стали горит неподвижная дуга, которую можно считать точечным непрерывно действующим неподвижным источником теплоты. Определить приращение температуры в точке на расстоянии R= 1,5 см спустя / = 20 с после начала нагрева прн t/=30B; /=200 А; к. п. д. г| = 0,7. По табл. 5.1 находим значение теплофизн - ческих коэффициентов: Х = 0,4 Вт/(см-К); а = 0,08см2/с. |
|
и и интегриру- ;i—Ф(«)]э (елі) |
|
а — точечный источник теплоты в полубеско - нечном теле; б — линейный источник теплоты в бесконечной пластине б = 1,2 см; в — плоский источник теплоты в бесконечном стержне F = — 8 см2 |
|
Точечный источник теплоты на поверхности полубесконечного тела. Предположим, что мгновенный точечный источник теплоты мощностью q действовал в течение бесконечно малого отрезка времени dt и с тех пор прошло время t. Тогда приращение температуры точек тела на основании уравнения (6.2) Если источник теплоты не прекращал своего действия в течение времени t, то приращение температуры определится путем интегрирования выражения (6.9) в пределах от О до t: . |
|
А Т= |
|
л < |
/г < |
Л |
|||
|
/С |
м |
||||
|
V |
2__ |
|
а) Т„К WOO 800 600 WO 200 |
Определяем эффективную МОЩНОСТЬ
q = ц VI = 0,7 • 30 • 200 = 4200 Вт.
Находим
ф(«) = ф(0,59) = 0,596.
Приращение температуры определяем по формуле (6.11)
4200
АГ=2.3,Т4.0,4-.1,5(1-°'596^450К-
Линейный источник теплоты в пластине. Рассмотрим случай линейного источника теплоты в пластине без теплоотдачи. Так же как и для точечного источника теплоты, из уравнения (6.6) находим приращение температуры:
dT = —e-'V(4*>. (6.12)
6ср(4лсЦ)
Интегрируем от 0 до t и вводим замену z= r2/(4at):
ДГ =
4яХ6
<-7(4af)
где Ei — интегральная показательная функция.
Изменение температуры во времени показано на рис. 6.3, б. В отличие от точечного источника теплоты в полубесконечном теле, где температуры отдельных точек стремятся к определенным значениям, в пластине температуры точек возрастают беспредельно. Непрерывное нарастание температуры объясняется тем, что в пластине тепловой поток стеснен и теплота не успевает перетекать в более холодные зоны. При наличии теплоотдачи с поверхностей пластины (см. п. 5.2) температуры точек стремятся к определенным конечным значениям.
Пример 2. Пластина из низкоуглеродистой стали толщиной 6 = 0,5 см нагревается неподвижной дугой мощностью q= 4000 Вт. Определить время, необходимое для нагрева на Д7" = 800К пятна диаметром 2 см. Теплофизические коэффициенты находим из табл. 5.1: X = 0,4 Вт/(см - К); а=0,08см2/с.
|
К-вг)- |
Используем формулу (6.13)
, ДГ4лХ5 800-4-3,14-0,4-0,5
* I ) =---------------- —- --------- 4000------- = -0’502-
По таблицам для интегральной показательной функции находим, что значение аргумента —r2/(4at) = — 0,55; / = г2/(4а-0,55)= 6 с.
Плоский источник теплоты в стержне. Рассмотрим случай нагрева плоским источником теплоты полубесконечного стержня без теплоотдачи. Поступая аналогично предыдущим случаям, из выражения (6.8) с учетом Ь = 0 находим приращение температуры:
dT= 2ЯЁ* e-*V(ta0. (6.14)
Fcp(4na<) 1
|
Интегрируя от 0 до t и вводя замены, находим
|
Так же как и в случае линейного источника теплоты, температура точек стержня беспредельно возрастает с ростом t (рис.
6.3, в). Нагрев тел неподвижными источниками теплоты, действующими бесконечно длительное время, рассмотрен в п. 6.2.
Неподвижный непрерывно действующий источник теплоты переменной мощности. Определение приращений температуры точек тела при действии источника теплоты переменной мощности принципиально ничем не отличается от ранее рассмотренных случаев с источниками теплоты постоянной мощности. Если мощность источника теплоты изменяется во времени, т. е. q = q{t), то необходимо взамен постоянной величины q в уравнения (6.9), (6.12) и (6.14) подставить функцию q(t), а затем провести интегрирование. Разумеется, при этом может оказаться, что интегралы взять невозможно. В таких случаях их определение следует производить численно, составляя таблицы или программу для ЭВМ.
Выравнивание температур. Определять температуру точек тела в процессе выравнивания, когда источник теплоты прекратил свое действие, можно двояко.
Во-первых, начальное неравномерное распределение температуры Тн можно рассматривать как некоторую температуру, возникшую вследствие выделения теплоты мгновенными элементарными источниками теплоты в момент времени t= 0. Зная закон распределения температуры от отдельного мгновенного источника теплоты, можно путем интегрирования по объему тела определить температуру от суммарного действия всех элементарных источников, т. е. описать процесс выравнивания температуры. Рассмотрим в качестве примера выравнивание температуры в бесконечном стержне сечением F, который при f=0 был нагрет до Тя на участке длиной 21; будем полагать, что остальная часть стержня находилась при Т = 0 (рис. 6.4). Выде-
Т
|
|
|
x-(x'+dx') х |
|
I |
|
I |
о
х
Рис. 6.4. Начальное распределение температуры 7"н в стержне на участке 2/
|
Рнс. 6.5. Процесс выравнивания температуры в неограниченном стержне, участок которого 21 = 2 см нагрет при / = 0 до 7'н= 1000/(; а = 0,1 см2/с: а — распределение температуры в различные моменты времени; 6 — кривые изменения температуры во времени, в — стержень |
|
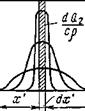
лим некоторый элементарный слой толщиной dx', в котором при /=0 содержится количество теплоты dQ = срТпЕ dx'. Будем рассматривать его как мгновенный плоский источник теплоты. Данный элементарный источник теплоты находится от рассматриваемой точки А на расстоянии х — {х’ --dx'). Следовательно, приращение температуры в точке А через время t от данного источ |
|
Процесс выравнивания описываемый уравнением ставлен на рис. 6.5. Второй прием, с помощью которого можно рассчитать процесс выравнивания, основан на использовании фиктивных источников и стоков теплоты. Его целесообразно применять в тех случаях, когда известен закон действия источника теплоты вплоть до начала процесса выравнивания. Например, известно, что на поверхности полубесконечного тела в течение времени t0 действовал точечный источник теплоты постоянной мощности q |
|
-MSS?*****'””- (*•'« Полная температура в точке А от всех элементарных источников определится путем интегрирования на участке от —I до cpT9dx’ |
|
;=^К#)-ф(дё=)] |
|
ника теплоты составит dTА |
|
dQ/F |
|
Тл4 |
|
е-(*-х')7(4аг) |
|
Ср(4яЩ)|/2 |
|
У4at ' (6.17) температуры, (6.17), пред- |
|
тпд ш |
|
I |
|
lift ,'Ki I |
|
1 .U |
|
t-t |
|
Рис. 6.6. Схема действия фиктивного источника / и фиктивного стока теплоты II для определения выравнивания температуры неподвижный (рис. 6.6). |
Искусственно можно представить, что после прекращения действия источника теплоты q продолжают действовать одновременно в одной и той же точке фиктивный источник теплоты q и фиктивный сток теплоты —q. Под стоком теплоты будем понимать такой источник теплоты, действие которого вызывает отрицательное приращение температуры. Фиктивный источник и фиктивный сток теплоты будут взаимно уничтожаться, т. е. будет соблюдаться условие о прекращении существования действительного источника теплоты начиная с момента времени t = t0. Изменение температуры в период выравнивания определится как разность приращений температур источника ДГИ и стока теплоты АД. Например, для точечного источника, используя выражение
(6.11) , находим
Д7’=ДГи-ДГс=-4-[ 1_ф(_5_У|
1_фГ _«—]} =
2лIR ( L ^4a(t-tо)
_{ф[---------------------------- * 1_ф(_«_и (6.18)
2nXR 1 L - v/4a(/-/o)J 4 УїоГ'
где t — время от начала действия источника теплоты до рассматриваемого момента времени; to — продолжительность действия источника теплоты.
Аналогично можно определить выравнивание температур после окончания действия линейного или плоского неподвижного источника теплоты.
Пример 3. Для условий примера 1 определить приращение температуры течки 7? = 1,5 см спустя 25 с после прекращения горения дуги. Время нагрева t0 =20 с.
Используем формулу (6.18). Полное время t — 45с.
|
АГ 4200 |
Э | Г 1,5 ] Г 1,5 ] 1
|
2-3,14-0,' = 1115[Ф(0,53)-Ф(0,4)]= 132 К. |
,4-1,51 L 4-0,08(45—20) J L 4-0,08-454 >