Поверхностная теплоотдача и граничные условия
Выше были сформулированы условия теплопередачи в твердых телах вследствие теплопроводности металлов. С поверхности металлов теплота передается конвективным путем или посредством радиации. Указанные процессы играют важную роль при сварке: в конечном итоге вся теплота, введенная при сварке, отдается в окружающее пространство и тела остывают.
КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
При конвективном теплообмене теплота с поверхности уносится жидкостью или газом, которые перемещаются относительно поверхности. Движение жидкости или газа может возникать вследствие различной плотности нагретых и ненагретых зон или в результате принудительной циркуляции жидкости и газа.
Приближенно тепловой поток <72к с единицы поверхности за единицу времени при конвективном теплообмене определяется по правилу Ньютона:
<?2к=ак(Г-Тс), (5-Ю)
где а*—коэффициент конвективной теплоотдачи; Т — температура поверхности твердого тела; Тс — температура среды (жидкости или газа).
Коэффициент — не постоянная величина, он может изменяться в широких пределах в зависимости от следующих факторов:
от свойств окружающей среды (теплопроводности, плотности, вязкости) и ее движения относительно поверхности;
от физических свойств поверхности, отдающей теплоту;
от формы поверхности тела и ее положения в пространстве;
от разности температур Т — Тс.
ЛУЧИСТЫЙ ТЕПЛООБМЕН
Тепловое излучение представляет собой электромагнитные колебания. Удельный поток излучения тела пропорционален четвертой степени его абсолютной температуры (закон Стефана — Больцмана):
<72 г=СяП; (5.11)
С, = еС0. (5.12)
Коэффициент Ся зависит от состояния поверхности тела и выражается через коэффициент степени черноты тела є. Для абсолютно черного тела е=1, а Св=/У0 = 57,6 НВт/(см2- К4). Большинство встречающихся в технике тел можно рассматривать как серые, у которых е<1. Значение є зависит от природы тела, характера поверхности и температуры. Для окисленных шероховатых поверхностей сталей є изменяется от 0,6 до 0,95. 6-923 145
У алюминия є изменяется от 0,05 до 0,2 в зависимости от свойств поверхности и температуры.
|
Рис. 5.6. Коэффициенты полной теплоотдачи а и лучистого теплообмена а, вертикальных листов углеродистой стали в зависимости от температуры при Гс = 273 К |
В реальных условиях нагретое тело окружено другими телами (помещение цеха, сварочные приспособления, изделия И др.). Между этими телами происходит взаимный лучистый теплообмен. Каждое тело излучает энергию и воспринимает часть энергии, излучаемой другими телами:
q2r = еС0(Р - Т?), .(5.13)
где Т — температура тела; Гс — температура среды.
Первый член в правой части уравнения (5.13) после раскрытия скобок выражает теплоту, излучаемую телом, второй — поглощаемую им.
По аналогии с выражением
(5.10) можно связать удельный тепловой поток q2, с разностью температур Т — Ті
qtr^OriT-P), (5.14)
где Or — коэффициент лучистого теплообмена.
Тогда удельный поток полной теплоотдачи можно представить как сумму удельных потоков конвективного и лучистого теплообмена:
^2 = оск(Г—7’с) + аг(7’—Гс) = а(7’ —Тс), (5.15)
где a=tXK-f-ar — коэффициент полной поверхностной теплоотдачи.
Коэффициент а значительно изменяется с ростом температуры (рис. 5.6).
При температурах до 400—500 К основная часть теплоты отдается конвективным, при более высоких температурах — лучистым теплообменом.
ГРАНИЧНЫЕ УСЛОВИЯ
Чтобы рассчитать изменение температуры точек тела во времени, кроме закономерности распространения теплоты в теле необходимо знать еще два условия:
условия теплообмена на границах тела — так называемые граничные условия;
начальное распределение температуры в теле при / = 0.
Граничные условия выражают тепловое взаимодействие поверхности тела с окружающей средой и могут быть весьма разнообразны. С практической точки зрения интересны следующие граничные условия.
Граничное условие 1-го рода определяет закон изменения температуры точек поверхности тела. Частный случай условия 1-го рода—изотермическое условие, когда поверхность тела обладает постоянной температурой в течение всего процесса распространения теплоты. Например, при интенсивном омывании поверхности тела жидкостью температура поверхности может оставаться постоянной. В расчетах тепловых процессов при сварке условие 1-го рода встречается относительно редко.
|
А |
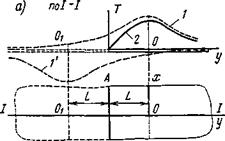
Приведем пример того, как можно с помощью некоторых формальных приемов удовлетворить изотермическому условию. Пусть полубесконечная пластина нагревается в точке О сварочной дугой (рис. 5.7, а), а температура Т границы А—А постоянно поддерживается равной нулю. Очевидно, что если бы пластина была бесконечной, то распределение температур в сечении I — /в некоторый момент времени выражалось кривой 1 и температура по линии А — Л не равнялась нулю. Однако можно представить, что в точке О і той же бесконечной пластины, находящейся также на расстоянии L от А — А, действует источник теплоты с отрицательным знаком, так называемый сток теплоты. Причем свойства этого стока теплоты в точности совпадают со свойствами источника теплоты от сварочной дуги, а распределение температур описывается одинаковым математическим выражением.
|
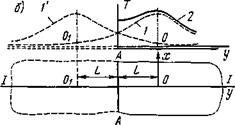
Рис. 5.7. Выполнение граничных условий: а — изотермического путем использования стока теплоты; б — адиабатического путем использования дополнительного источника теплоты |
Тогда отрицательная температура выразится кривой 1', аналогичной кривой 1, но с отрицательным знаком. Складывая ординаты кривой 1' с ординатами кривой /, получим кривую 2 распределения температуры. На границе А —А температура всегда будет постоянна, в то время как в самой пластине температура точек будет непрерывно меняться.
Условие 2-го рода определяет значение тепло
вого потока не границе тела. Если вспомнить, что закон теплопроводности выражает связь между тепловым потоком и градиентом температур, то станет понятным, что условие 2-го рода задает градиент температуры на границе тела.
Адиабатическая граница представляет собой частный случай условия 2-го рода, когда тепловой поток с поверхности тела равен нулю, т. е.
qs = 0; дТ/дп3 = 0.
В технических расчетах, в частности применительно к сварке, нередко встречаются случаи, когда тепловой поток с поверхности тела мал по сравнению с потоками внутри тела. Тогда можно считать эту границу адиабатической.
Например, при нагреве сварочной дугой полубесконечной пластины в точке О (рис. 5.7, 6) граница А—А соприкасается с воздухом и излучает некоторое количество теплоты. Для простоты расчетов можно принять, что граница А — А теплонепроницаема, т. е. адиабатична. Выполнить это условие можно, пользуясь формальным приемом. Допустим, что пластина бесконечна и в ней на расстоянии L по другую сторону от линии А — А в точке 0 действует точно такой же источник теплоты, как и в точке О. Очевидно, что тепловой поток через границу А — А от источника О равен в каждой точке линии А — А тепловому потоку от источника 0. Суммарный тепловой поток через границу А — А, следовательно, равен нулю. Температуру точек полубесконечной пластины находят путем сложения ординат кривой 1 с ординатами кривой V (рис. 5.7,6). Температура края полубесконечной пластины оказывается вдвое больше температуры соответствующих точек бесконечной пластины. Описанный прием компенсации теплового потока носит название метода отражения, так как в этом случае теплонепроницаемая граница может рассматриваться как граница, отражающая тепловой поток, идущий со стороны металла.
Условие 3-го рода определяет теплообмен на границе тела и среды с заданной температурой. По правилу Ньютона,
fe = o(7’-rc), (5.16)
гДе <72s —■ удельный тепловой поток через граничную поверхность; Т — температура точек поверхности тела; Тс — температура среды.
Очевидно, что по закону теплопроводности к границе поступает теплота q2= —кдТ/дп, при этом q2s=q2.
Из условия 3-го рода как предельные случаи могут быть получены изотермическое и адиабатическое условия. Если Я — некоторая конечная, не равная нулю величина, то при а->-оо условие будет изотермическим, а при а->-0 — адиабатическим.
Применение граничного условия 3-го рода проиллюстрируем примером свободного охлаждения тонкой пластины. Задаемся граничными условиями:
1. Начальное распределение температуры в пластине равномерно, т. е. при (=0 Т=Т„.
2. Краевое условие зададим по правилу Ньютона:
q2S=a{T-Tc). (5.17)
За время dt с двух поверхностей пластины 2F будет отдано в окружающую среду количество теплоты
dQ=qs2Fd(=a(T—Tc)2Fdt. (5.18)
Температура пластины объемом бF с теплоемкостью материала ср за время dt понизится на величину dT:
dT=dQ/{cp6F). (5.19)
Подставляя выражение (5.18) в (5.19) и преобразуя, находим dT/(T—Tt) = — [ 2а/(срб)] = - bdt. (5.20)
Величина Ь = 2а/(ср6) носит название коэффициента темпе - ратуроотдачи для пластины и имеет размерность 1 /с.
Интегрируя (5.20), находим
In {Т-Тс)=-Ы + С. (5.21)
Постоянную интегрирования С определим из начального условия Т=Т„ при t = 0:
С=1п(Г„= Тс) (5.22)
Подставляя С в уравнение (5.21) и потенцируя, находим
Т-Тс = {Та-Тс)е~ь‘. (5.23)
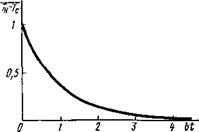
Закон изменения температуры, описываемый экспонентой е~ь‘, графически показан на рис. 5.8.
Пример 1. Перед сваркой пластины из стали толщиной 6 = 40 мм были подогреты до 7'„ = 550К. Определить, в течение какого времени пластины будут сохранять температуру Т не ниже 500 К; тепловыделением при сварке пренебречь. На рис. 5.3 находим для Т = 500...
|
Т-Тп
Рис. 5.8. Изменение во времени температуры равномерно нагретой пластины в процессе свободного охлаждения |
550 К с = 0,55 Дж/г-К; подставляя р = 7,8 г/см3, получим ср = 0,55-7,8 = = 4,29 Дж/(см3-К).
На рис. 5.6 находим для Т « ж*500...550 К а = 2,5- 10“3 Вт/(см2Х ХК); Ь = 2а/(срб) = 2 • 2,5- 10"3/ /(4,29X4) =2,91 • 10-41 /с.
Из выражения (5.23) находим при Tz = 300 К
е~ы = (Г — 7'с)/(7'н — Тс)', —Ы =
= 1п[(Г-7с)/(Ги-7-с)] =
|
0,2232 ‘ = ~2ДГИГ7- = 767 С : |
= 1п(200/250) = — 0,2232. Определяем t: