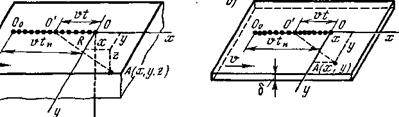Движущиеся источники теплоты
Для составления уравнений, описывающих процесс распространения теплоты от движущихся непрерывно действующих источников, используют принцип наложения. С этой целью весь период действия источника теплоты разбивают на бесконечно малые отрезки времени dt. Действие источника теплоты в течение бесконечно малого отрезка времени dt представляют как действие мгновенного источника теплоты. Суммируя процессы распространения теплоты от действующих друг за другом в разных местах тела мгновенных источников теплоты, получают уравнение температурного поля при непрерывном действии движущегося источника теплоты.
ТОЧЕЧНЫЙ ИСТОЧНИК НА ПОВЕРХНОСТИ ПОЛУБЕСКОНЕЧНОГО ТЕЛА
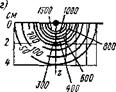
Точечный источник теплоты постоянной мощности q движется с постоянной скоростью v прямолинейно из точки О о в направлении оси х (рис. 6.7, а). Допустим, что с момента движения источника прошло время tH и он находится в точке О. Вместе с источником теплоты перемещается подвижная система координат, начало которой совпадает с местоположением источника теплоты, т. е. с точкой О. Требуется определить приращение температуры точки А{х, у, z).
Для этого запишем приращение температуры в точке А от мгновенного точечного источника теплоты, который действовал в течение времени dt в точке О'. С момента выделения теплоты в точке О' прошло время t. Используем уравнение (6.2), полагая
Q = qdt, а расстояние О'А = sj{x + vt)‘2+ у2+ z2. Тогда
|
(6.19) |
(*+1>02+уЧг*
|
|
Суммируем приращения температуры от всех элементарных источников теплоты на линии ОО0. Время распространения теплоты от мгновенного источника в точке О равно нулю, а от мгновенного источника в точке Оо равно tn. Поэтому интеграл берем в пределах от 0 до tK:
|
(*+оОЧуЧ2*
|
(6.20)
|
|
|
а) * |
|
Я |
|
2 |
|
В) Оо 0' О А(Х)
Рис. 6.7. Схема движения непрерывно действующего источника мощностью q, перемещающегося со скоростью и: а — точечный на поверхности полубесконечного тела; б — линейный в бесконечной пластине; в — плоский в бесконечном стержне |
После преобразований получим
|
|
|
4 о 4а/ |
(6.21)
где /?2 — х24-у24-z2 (рис. 6.7, а).
Уравнение (6.21) выражает приращения температур в полубесконечной теле в стадии теплонасыщения, т. е. когда температура отдельных точек непрерывно повышается. Приращение температуры в стадии теплонасыщения численно определяют по номограмме, приведенной в п. 6.3.
Предельное состояние. После продолжительного действия источника теплоты достигается так называемое предельное состояние, когда температура точек в подвижной системе координат перестает изменяться во времени. Такое состояние достигается при £н—>-оо и называется квазистационарным.
В этом случае уравнение (6.21) интегрируется после подстановки R2/{Aat) = и и принимает вид
|
|
(6.22)
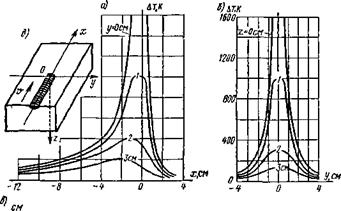
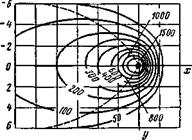
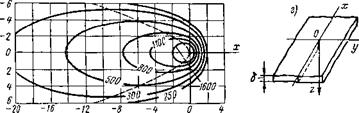
Температурное поле предельного состояния симметрично относительно оси Ох (рис. 6.8). Изотермы на поверхности хОу представляют собой овальные кривые, которые сгущены впереди источника теплоты и раздвинуты позади него (рис. 6.8, а). Изотермические поверхности как бы образованы вращением изотерм относительно оси Ох. Смещенность изотерм относительно друг друга и их вытянутость зависят от безразмерного параметра vR/(2a). В области малых значений vR/(2a) изотермы близки к окружностям, при больших значениях они вытянуты вдоль оси Ох.
Распределение приращения температуры по поверхности массивного тела на расстоянии у, равном 1, 2, 3 см, представлено соответствующими кривыми на рис. 6.8, в. Температура точек при приближении источника теплоты резко возрастает, достигает максимума, а затем убывает. Снижение температуры происходит с меньшей скоростью, чем ее подъем. Максимум температуры в точках, находящихся не на оси Ох, достигается после прохождения источником теплоты плоскости, параллельной yOz, в которой находится рассматриваемая точка. В более удаленных от оси Ох точках максимальная температура достигается позже и имеет меньшее численное значение по сравнению с точками, расположенными ближе к оси Ох. Штриховой линией на рис. 6.8, а соединены точки с максимальной температурой на плоскости хОу. Поверхность раздела областей нагрева и остывания получается путем вращения штриховой кривой относительно оси Ох. Область впереди штриховой кривой нагревается, позади — остывает.
|
|
|
|
|
Рис. 6.8. Приращение температур в предельном состоянии при движении точечного источника теплоты на поверхности полубес- конечного тела д = 4000Вт, v — 0,1 см/с, а = 0,1 см2/с, Х = = 0,4 Вт/(см*К) ]: а — изотермы на поверхности хОу (штриховая кривая разделяет область нагрева и область остывания), б — изотермы в поперечной плоскости xOz, проходящей через центр источника; в — распределение приращений температуры по прямым, параллельным оси х и расположенным на поверхности массивного тела, г — распределение приращений температуры по прямым, параллельным оси у н лежащим в поперечной плоскости xOz; д — схема расположения координатных осей |
|
|
Неподвижный источник теплоты. Если в уравнении (6.22) и = 0, то это будет случай стационарного температурного поля в полубесконечном теле
АТщ=д/(2яХЯ). (6.23)
Температура в направлении от источника теплоты убывает обратно пропорционально R, т. е. по закону гиперболы. Приращения температуры на данном расстоянии R прямо пропорциональны мощности источника теплоты q и обратно пропорциональны коэффициенту теплопроводности к. Распределение температуры не зависит от теплоемкости материала ср.
Пример 4. По поверхности массивного тела движется точечный источник теплоты мощностью 6000 Вт. Определить расстояние от источника теплоты до конца изотермы Д7'= 700 К. Коэффициент теплопроводности металла X — = 0,4 Вт/(см-К).
Используем формулу (6.22). Так как позади источника теплоты по оси R=—x, то ДТнр = q/(2nXR), откуда R= q/(2nXTn?) = 6000/(2-3,14-0,4-700) = = 3,44 см.
ЛИНЕЙНЫЙ ИСТОЧНИК В БЕСКОНЕЧНОЙ
ПЛАСТИНЕ
Линейный источник теплоты мощностью q с равномерным распределением ее по толщине пластины движется с постоянной скоростью и (см. рис. 6.7,6). Граничные плоскости z = 0 и z — 8 отдают теплоту в окружающую среду, температуру которой Тс принимаем равной начальной температуре тела Г„. Коэффициент теплоотдачи а.
Уравнение, описывающее приращение температур в пластине, получим так же, как в случае точечного источника теплоты. Приращение температуры в точке А от мгновенного линейного источника теплоты, который действовал в точке О', составит в соответствии с уравнением (6.6)
dT= ■ Ne ш. (6.24)
6cp(4nat)
Интегрируя от 0 до и преобразовывая, получим
VX / v7 г1
ДТ=-Э—е~~^ (6.25)
4яМ> JQ t к '
где г2 = х2--у2.
Уравнение (6.25) выражает приращение температур в пластине в стадии теплонасыщения. Предельное квазистационарное состояние достигается при оо. В этом случае уравнение (6.25) интегрируется и принимает вид
<6-26>
где Ко—функция Бесселя 1-го рода нулевого порядка;
Ь = -~ (см. п. 5.2 и 6.1).
срб v ’
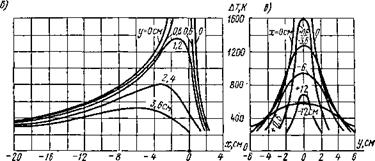
Предельное состояние. При нагреве пластины линейным источником теплоты распределение температуры по ее толщине согласно уравнению (6.26) равномерно. Следует, однако, иметь в виду, что в действительности из-за наличия теплоотдачи с поверхности пластины всегда наблюдается некоторая неравномерность распределения температуры по ее толщине. Эта неравномерность будет тем значительнее, чем больше величина 4ba/v2. Кроме того, при расчете температуры с учетом теплоотдачи коэффициент теплоотдачи а принимался не зависящим от темпера-
а)
|
у£м
|
|
Рис. 6.9. Приращение температур в предельном состоянии при движении линейного источника теплоты в бесконечной пластине [<7 = = 4000 Вт, v = 0,1 см/с, 6 = 1 см, а = 0,1 см2/с; X = 0,4 Вт/ (см • К), Ь = 2,8-1031 /с]: а — изотермы на поверхности пластины (штриховая кривая — точки с максимальными температурами); б — распределение приращений температуры в сечениях, параллельных оси х; в — распределение приращений температуры в сечениях, параллельных оси у; г — схема координатных осей |
туры и имел некоторое среднее значение. Фактически это означает, что в области высоких температур теплоотдача на самом деле будет происходить интенсивнее, а в области низких температур слабее, чем это получается из расчета.
Картины распределения приращения температуры в пластине (рис. 6.9) и в плоскости хОу массивного тела (см. рис. 6.8) качественно имеют много общего. Отличие заключается в том, что изотермы в пластине еще более вытянуты, чем в полубеско - иечном теле. Степень вытянутости изотерм зависит не только от условий сварки и теплофизических свойств материала, но и от теплоотдачи в воздух.
Неподвижный источник. Если в уравнении (6.26) принять v = 0, то получим уравнение стационарного температурного поля в пластине:
|
(6.27) |
|
А Г, |
|
К |
|
пр |
|
2яХб |
|
(л/?)- |
Температурное поле осесимметрично. В отличие от полубеско - нечного тела, где стационарное состояние достигается благодаря значительному теплоотводу в трех направлениях, стационарное состояние в пластине возможно лишь при наличии теплоотдачи в окружающее пространство. Если теплоотдача отсутствует, т. е. б-v0, температура АТпр возрастает беспредельно, так как при
V6F/W0 значение функции Ка{л1 Ьг2/а) стремится к бесконечности. Распределение температуры при стационарном процессе в пластине зависит не только от мощности и коэффициента теплопроводности К, но и от коэффициента теплоотдачи а и толщины пластины 6.
Пример 5. Построить график изменения температуры в пластине на участке от *=2 см до х=—8 см, р= 2 см (см. рис. 6.7,6) при нагреве ее движущимся линейным источником теплоты, когда достигнуто предельное квазистационар - ное состояние; (?=4000Вт, п = 0,1 см/с, 6=1 см; а = 0,085 см2/с, Х=0,42 Вт/(см-К); ср = 4,9 Дж/(см3-К).
Коэффициент теплоотдачи а находим по графику, приведенному на рис. 5.6 для Т=900 К; а=6- 1(Г3 Вт/(см2-К).
Перед вычислением определяем необходимые коэффициенты:
6 = 2а(ср6) = 2,45-10-3 с-1; V v'^/^a'1) + Ь/а = 0,612 см-1;
—о/(2а)= -0,59 см"'; q/(2лЩ = 1515 К-
Температуры определяем для точек х=2 0; —2; —4; —6; —8 см по формуле (6.26). Для удобства вычислений результаты вносим в таблицу в такой последовательности:
|
X., СИ |
г, см |
-vx/{2 а) |
е-«/(2.) |
и = г |
Ко («•) |
А Г, к |
|
Уй+А v 4 а а |
||||||
|
2 |
2,83 |
— 1,18 |
0,307 |
1,73 |
0,1593 |
74 |
|
0 |
2 |
0 |
1 |
1,22 |
0,310 |
470 |
|
_ 2 |
2,83 |
+ 1,18 |
3,25 |
1,73 |
0,1593 |
785 |
|
—4 |
4,47 |
+2,36 |
10,59 |
2,73 |
0,0476 |
763 |
|
-6 |
6,32 |
+3,54 |
34,46 |
3,87 |
0,0129 |
673 |
|
—8 |
8,23 |
+4,72 |
112,2 |
5,03 |
0,00357 |
607 |
При больших значениях аргумента и = r-^v‘2/(4а2) 4- Ь/а (свыше 10) значения Ко(и) можно вычислять по асимптотической формуле
Ко (и) » e-“VvM11 - 1/(8и)].
ПЛОСКИЙ ИСТОЧНИК В БЕСКОНЕЧНОМ СТЕРЖНЕ
Представим, что плоский источник теплоты ПОСТОЯННОЙ мощности q равномерно распределен по поперечному сечению стержня F и перемещается с постоянной скоростью v в направлении вдоль стержня (см. рис. 6.7, б). Боковая поверхность отдает теплоту в окружающую среду при постоянном коэффициенте теплоотдачи а.
Приращение температуры в точке А от мгновенного плоского источника, который действовал в точке О' t с назад, составит
|
qdt |
|
dT |
|
(6.28) |
|
Fcp (4ла<)1, |
|
о—(* + »OV(4oO — bt |
Начало координат движется вместе с источником теплоты и находится в точке О.
Интегрируем приращения температуры от всех мгновенных источников теплоты в пределах от 0 до t„-
|
■(£ + *)' |
|
л ,1/2 |
|
-27* |
|
(6.29) |
|
cpF (4яа)1/2 |
|
А Г =• |
Уравнение (6.29) описывает приращение температуры в пластине в стадии теплонасыщения. Предельное квазистационарное состояние достигается при t„ оо. В этом случае уравнение (6.29) после введения замены t = и2 и интегрирования принимает вид
|
ух -“Ъ5- V |
|
1 + ■ |
|
* 2а 2а~ |
|
(6.30) |
|
где b - -21L cpF |
|
cpvF^J 1 + 4 ba/v2 (см. п. 6.1 ) . |
|
АТ =■ |
Предельное состояние. При нагреве стержня плоским источником теплоты распределение температуры по поперечному сечению стержня согласно уравнению (6.30) равномерно. В действительности из-за теплоотдачи с поверхности стержня всегда будет наблюдаться некоторая неравномерность распределения температуры по его поперечному сечению.
Распределение температуры вдоль стержня будет характеризоваться быстрым нарастанием температуры впереди источника теплоты и весьма плавным спадом температуры позади источника (рис. 6.10). Если 4ba/v2 — 0, т. е. теплоотдача отсутствует,
. то температура позади ис
|
— 0,8 ПК |
|||||
|
4 0,1 |
0,15 |
||||
|
ЇЬа/у |
Ц05 |
||||
|
лТ |
|
-УХ Za |
|
-10 -8 -6-ї |
|
-г |
|
УХ 2а |
точника теплоты будет оставаться постоянной.
|
• - yjbx2ja |
Неподвижный источник. Если в уравнении
(6.30) v = 0, то получим уравнение стационарного температурного поля в стержне:
ЬТ пр =
~2cpF-Jba
(6.31)
|
Рис. 6 10. Распределение приращений температуры по длине стержня при движении плоского непрерывно действующего источника |
Стационарное состояние в стержне возможно лишь при наличии теплоотдачи в окружающую
среду. Распределение приращений температуры при стационарном процессе в стержне зависит от к, b, F и eg.