Быстродвижущиеся источники теплоты
В сварочной технике все чаще применяются мощные источники теплоты, осуществляющие сварку с весьма большими скоростями. В предельном случае, когда q и v стремятся к бесконечности, в то время как отношение q/v сохраняет некоторое конечное значение, распространение теплоты в массивном теле и пластине приобретает особенности, позволяющие значительно упростить расчетные схемы.
ТОЧЕЧНЫЙ источник
Упростим уравнение предельного состояния (6.32), налагая условия
q^~oo, v -*■ оо, q/v = q„ = const, (6.39)
где qn — погонная энергия.
|
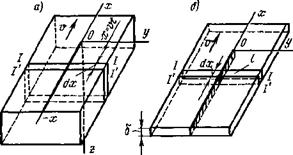
Рис. 6.13. Схема выделения плоскостями / и /' зон распространения теплоты от мощного быстродвнжущсгося источника: а — точечный источник на поверхности полубесконечиого тела; б — линейный источник в бесконечной пластине |
Очевидно, что уравнение (6.22) для области позади источника, теплоты, где а:<0, можно преобразовать с учетом R=-j х2 у'2 г2 и х = — vt к следующему виду:
а,*(-> +ЫТ+(!,1+г*)/у*
ДГ =------- Є к (6.40)
2лЛ. V/2 Ч" (^2_Ь2^)/у '
где t — время, отсчитываемое от момента, когда источник теплоты пересек перпендикулярную оси Ох плоскость /, в которой расположена рассматриваемая точка (рис.6.13, о). .
Так как при v -*■ оо величина (у2 + z2)/v2 мала по сравнению с t2, то
V^+V + г2)/^2 * ( + (У2 + z2)/{2v2t). (6.41)
После преобразований, пренебрегая бесконечно малой величиной, находим
ST =—е-(г/2+2г)/(4о()_ (6.42)
2я Xt
Уравнение (6.42), не содержащее координаты х, указывает на то, что тепловые потоки в направлении, параллельном оси Ох, вдоль которой движется источник теплоты, ничтожно малы по сравнению с тепловыми потоками в перпендикулярном направлении, так как дТ/дх = 0. Это справедливо при v оо. Однако уравнение (6.42) может использоваться для технических расчетов, когда скорость v, хотя и не стремится к бесконечности, но достаточно велика. В этом случае применяют замену
t = — x/v.
Тогда
д т ------- 2—е-гЧ^)- (6.43)
Если из выражения (6.43) найти величину д2Т/дх2, пропорциональную разности тепловых потоков, проходящих через плоскости / и I ' в направлении Ох, и записать ее в функции v и t, то обнаружится, что количество теплоты, поступающей в слой между плоскостями / и Г при конкретном I, сильно зависит ОТ V. Чем больше v, тем меньше влияние тепловых потоков вдоль оси Ох на распределение приращений температур в плоскости yOz.
Процесс распространения теплоты почти полностью зависит от тепловых потоков в плоскости yOz. Такое физическое представление о процессе распространения теплоты позволяет получить уравнение (6.42) другим, довольно наглядным способом. Точечный источник теплоты, проходя через плоскость / (рис. 6.13, а), выделяет на участке dx в течение времени dx/v количество теплоты Q = qdx/v. Эта теплота распространяется в по - лубесконечном плоском слое Г — I толщиной 6 = dx, и, следовательно, для описания процесса распространения теплоты можно использовать уравнение (6.6) для бесконечной пластины с учетом того, что слой Г—/ представляет собой полубесконечную пластину без теплоотдачи (Ь —
|
|
= 0), а количество теплоты в этом случае равно 2Q. Подставляя величины 2Q = 2qdx/v и 6 в уравнение (6.6), получаем уравнение (6.42).
Для определения приращений температуры точек, расположенных позади источника теплоты, можно использовать
|
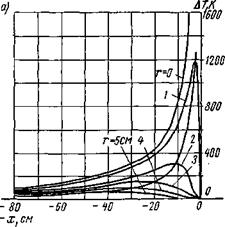
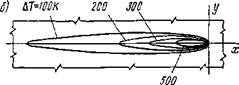
Рис. 6.14. Распределение приращений температуры при движении мощного быстродвижу - щегося точечного источника по поверхности массивного тела (q = 21 кВт, v = 1 см/с): а — распределение приращений температуры по линиям, параллельным оси Ох; 6 — изотермы иа поверхности тела |
уравнения (6.42) или (6.43). При использовании уравнения (6.42) необходимо иметь в виду, что для каждой поперечной плоскости I полубесконечного тела принимается свое время t, отсчитываемое с момента прохождения источника теплоты через рассматриваемую плоскость.
Приведенное на
рис. 6.14 распределение приращений температуры, описываемое уравнением (6.42), в области остывания мало отличается от распределения, описывае-
мого уравнением (6.22), действительным при любой скорости перемещения источника теплоты. Уравнением (6.42) не следует пользоваться в области малых значений t, соответствующих зоне выделения теплоты.
ЛИНЕЙНЫЙ источник
Предельное состояние процесса распространения теплоты при нагреве пластины мощным быстродвижущимся линейным источником теплоты также можно получить из уравнения (6.26) при условии (6.39). Ход рассуждений, основанный на предположении, что теплота распространяется только в направлении стержня 1 (см. рис. 6.13,6), такой же, как для случая точечного источника теплоты. Действительно, источник выделяет на отрезке длиной dx теплоту Q = qdxjv. Эта теплота распространяется вдоль стержня /, ограниченного плоскостями / и Г и имеющего поперечное сечение bdx. Подставляя указанные величины в уравнение (6.8) и заменяя координату х координатой г/, а также учитывая поверхностную теплопередачу, получим
АТ = J е-у'п* *)-»<, (6.45)
v8^J4nlcpt
где b — 2а/(ср6).
Если тела имеют начальную температуру Ги, то для определения абсолютной температуры взамен уравнений (6.42) и (6.45) используют следующие уравнения:
Т = -3-е~'2^+ Гн; (6.46)
2яА(
То =----------- -2--------- е-у*/(ш)-ы+ Tw (6.47)
vh^finXcpt
где Ти—начальная температура или температура подогрева тела.
Пример 6.8. Пластины из низколегированной стали толщиной 6 = 8 мм сваривают с подогревом при Т„ = 450 К дуговой сваркой под флюсом при токе /= 250 А, напряжении дуги (/ = 34 В и скорости о = 18 м/ч. Эффективный к. п.д. источника ч = 0,8. Определить температуру точки околошовной зоны с координатами относительно движущегося источника х = — 20 см, у — 3 см и температуру оси шва в том же сечении. .
По табл. 5.1 находим значения теплофизических коэффициентов а = = 0,08 см2/с, X = 0,39 Вт/(см-К), ср = 4,9 Дж/(см3-К), по графику, приведенному на рис. 5.6, — а « 6-10~3 Вт/(см2-К).
Эффективная мощность дуги
q = ЦШ = 0,8-34-250 = 6800 Вт,
скорость сварки v = 18 м/ч = 0,5 см/с.
Определяем коэффициент температуроотдачи
Ь = 2а/(сР6) = 2-6-10“7(4,9-0,8) = 3,06-10“3 с-'.
Время, прошедшее с момента прохождения источника теплоты через плоскость, в которой находятся заданные точки, определим через расстояние х и скорость сварки о:
t = — x/v — — ( —20)/0,5 = 40 с.
Температуру точки околошовиой зоны с координатой у — 3 см определим по формуле (6.47):
|
+ 450 = |
|
Т = • |
6800e~3 /И-0,08-40)—3,06- 10 • 40 0,5 • 0.8V4-3,14-0,39-4,9-40
= 548е-0,70 0,122 + 450 = 548-0,438 + 450 = 690 К.
Температура оси шва по формуле (6.47) при у = 0
Т = 548е-°122 + 450 = 548-0,885 + 450 = 935 К-