СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Примеры на синтез систем управления
Пример 2.12. Управление устройством электрической тяги
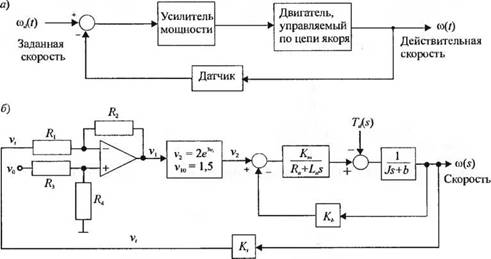
Большинство современных поездов дальнего и пригородного сообщения работают на электрической тяге. На рис. 2.35(a) изображена функциональная схема системы управления приводом электровоза, предназначенная для обеспечения заданной скорости движения. Цель синтеза состоит в получении модели системы, ее передаточной функции в замкнутом состоянии,
a) (s)/to/s), выборе надлежащих номиналов резисторов Rt, R2. R-$ и R4 и предсказании характеристик системы.
Первый шаг состоит в получении передаточной функции каждого блока. В качестве датчика скорости мы используем тахогенератор, выходное напряжение которого. V„ пропорциональное скорости, подадим на один из входов дифференциального усилителя, как показано на рис. 2.35(6). Усилитель мощности обладает нелинейной характеристикой, которая приближенно может быть описана зависимостью v2 = 2e3v‘ = 2exp(3v,) = gCv,). Рабочей точке на этой
|
|
|
|
|
Рис. 2.35. Система управления скоростью электропривода |
характеристике соответствует значение v)0 = 1.5 В. Воспользовавшись методом, изложенным в разд. 2.3, получим линейную модель усилителя мощности:
|
ФОі) |
|
|
dvx |
v10. |
Ay, = 2[3 exp(3v|0 )]Av, = 540Av, . (2.105)
Далее, отбрасывая символы приращений и воспользовавшись преобразованием Лапласа, получим:
V2(s) = 540 Г, (5).
Для дифференциального усилителя можно записать:
l+R7/R, r7
v, =------ 2-3-v0 —2 у (2.106)
1+R3/R4 й.
Потребуем, чтобы входной управляющий сигнал v() численно был равен заданному значению скорости, т. е. to,/=v0, где ш(/ измеряется в рад/с. a v0 — в вольтах. Тогда, если v0 = 10 В, то установившееся значение скорости должно быть равно 10 рад/с. Заметим, что в установившемся режиме v, = К, iad и следует ожидать, что выходное напряжение дифференциального усилителя будет равно
1+ RJiRl Rj
Vi =----- = ~V0 Л * Vii. (2.107)
1 1 +Rj/R4 Rt
Когда система находится в равновесии, то V| = 0 и если К, = 0,1, то
1 + RУ?2
1 +/?3/л4 л.
Это условие выполняется, если R2!R = 10 и R3/Rd = 10. Параметры двигателя и нагрузки приведены в табл. 2.7.
Таблица 2.7. Параметры мощного двигателя постоянного тока
Кт = 10 J = 2
Ra = 1 Ъ = 0,5
U= Кь = 0,1
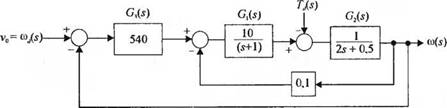
Полная схема системы изображена на рис.2.3 5(6). Используя формулу Мейсона, по сигнальному графу на рис.2.35(г) получим:
сф) _ 540С|(дХ^2(^ 540G|G2
0)^(5) 1 + 0,1 G|G-> + 540 G|G? 1+ 540,1 G(G^
5400 5400 2700
(2.108)
(5+ l)(2s + 0.5)+ 5401 2s2 + 2.5s + 5401,5 s2 + 1,25s + 2700,75
Поскольку характеристическое уравнение имеет второй порядок, то можно видеть, что ыи = 52 и С, = 0,012, т. е. следует ожидать, что реакция системы будет сильно колебательной.
Пример 2.13. Механический акселерометр
На рис. 2.36 изображен механический акселерометр, предназначенный для измерения ускорения салазок, подвешенных на магнитной подушке. Эти салазки от направляющего рельса отделяет зазор величиной 8. Измерение ускорения салазок a(t) обеспечивается за счет того, что положение у массы М относительно корпуса акселерометра пропорционально ускорению этого корпуса (и, соответственно, салазок). Задача состоит в синтезе акселерометра, обладающего заданными динамическими характеристиками. В частности, желательно, чтобы результат измерения, y(t) = qa{t), где q = const, был достигнут за приемлемое время.
|
Акселерометр |
|
Реактивный двигатель |
1---- ► х - положение корпуса
|
— у -------------- ► |
||
|
к |
||
|
и |
Hh |
|
|
Пружина |
ъ |
|
Корпус |
|
|
|
Салазки на магнитной подушке массой Ms |
|
Зазор 8 /____ |
Направляющий рельс
Рис. 2.36. Акселерометр на базе салазок с реактивным двигателем
Сумма сил. действующих на массу, равна
-Ь^--ку=М^{у+х), dt dt
или
,, d2y , dy,, d2x
M—%-+b—+ky=-M—г-. (2.109)
dt dt dt2
Поскольку сила, развиваемая реактивным двигателем, равна
F(t) = Ms~.
dt~
то
Му+ by+ky = -^-F(t).
М,
У* Ті У* Ті (2110)
м м Ms
Зададимся значениями ЫМ= 3, к! М= 2. обозначим F(t)/Mx = Q(t) и примем начальные условия у(0) = -1 и у(0) = 2. Если внешнее воздействие и. следовательно. Q(l) есть ступенчатая функция, то преобразование Лапласа последнего уравнения дает:
(s2Y(s) - sy(0) - j<0)) + 3(аУ(*) - ЯО» + 2Y(s) = - Q(s). (2.111)
Поскольку Q(s) = P/s. где P — амплитуда ступенчатой функции, то
CAXs)+ s - 2)+ 3(іУ(і)+ 1)+ 2Г(і) = -- ,
s
или
с?2 + 35 + 2)Г(д) = -(S +s+P (2.112)
Таким образом, преобразование Лапласа для выходной переменной имеет вид:
|
(s + S+ Р) |
|
(2.113) (2.114) |
|
s(s + Зі’ + 2) s(s + l)(s + 2) Разложение этого выражения на простые дроби дает: V/ к к2 ^3 s j+1 s+ 2 Дальнейшие действия дают следующее: |
|
(.s2+s+P) |
|
Y(s) = - |
|
Р ~2 ' |
s + s+ Р
|
(2.115) |
к, =-
(s + l)(s + 2)
Р+ 2
Аналогично. к2 = Р и =
. Таким образом, z
Р Р Р+ 2
|
(2.116) |
Y(s) = ~-- + —---
2s s + 1 2(s + 2)
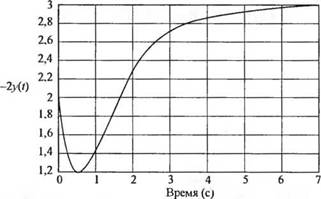
Следовательно, измеряемое значение выходной переменной равно ></) = -[-Я + 2Ре~' -(Р+ 2)ё~2' ], 1> 0.
График y(t) для Р = 3 представлен на рис. 2.37. Как видно из графика. y(t) становится пропорциональным величине силы спустя 5 секунд. Если это время считается недопустимо большим, то следует увеличить жесткость пружины к и коэффициент трения b с одновременным уменьшением массы М. Если выбрать значения ЫМ = 12 и к/М = 32, то акселерометр будет обеспечивать правильные показания через 1 секунду. (Читателю предоставляется возможность убедиться в этом самостоятельно.)
|
|
|
Рис. 2.37 Реакция акселерометра |
Пример 2.14. Синтез лабораторного работа
В этом примере мы попытаемся показать все сложности реального проектирования лабораторного устройства. Одновременно мы представим ряд элементов, которые обычно входят в состав систем управления.
Робот, предназначенный для использования в лабораторных условиях, показан на рис. 1.16. Рабочее пространство робота должно позволять ему достигать любой точки и манипулировать имеющимися в распоряжении приспособлениями. Кроме того, должна быть предусмотрена достаточная площадь для складирования материалов, не участвующих в текущих операциях. Лабораторный робот может выполнять три типа задач в процессе исследований. Первая задача состоит в том, что роботу поручается захватывать различные подносы, каркасы и контейнеры
и вносить их в рабочую зону. Второй круг задач включает в себя транспортировку образцов между пунктами приготовления химических препаратов и их анализа. В третьей группе задач роботу предоставляется возможность имитировать работу человека-оперетора в процессе различных лабораторных экспериментов.
Фирма Хьюлетт-Паккард создала лабораторный робот ORCA, смонтированный на рельсовых направляющих, имеющий антропоморфную руку, оптимально приспособленную для аналитических операций. Рельс может быть расположен как спереди, гак и сзади рабочего пространства. либо по его центру, если необходим доступ по обе его стороны. С помощью простой программы рука робота может перемещаться с одной стороны рельса на другую, сохраняя ориентацию кисти (чтобы переносить открытый контейнер) или фиксируя угловое положение кисти (при переносе объектов с произвольной ориентацией). Прямолинейная геометрия, в отличие от цилиндрической геометрии многих роботов, дает больше возможностей для размещения предметов в рабочем пространстве и установки самого робота в лаборатории. Движение всех сочленений координируется программными средствами, которые облегчают использование робота, задавая его ориентацию в более привычных декартовых координатах.
Основные технические характеристики робота ORCA приведены в табл 2.8.
|
Таблица 2.8. Технические характеристики робота ORCA
|
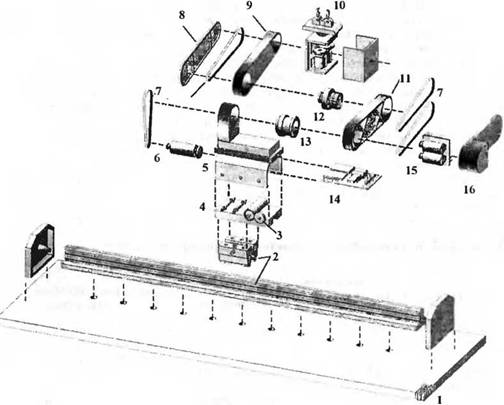
Синтез лабораторного робота ORCA заключался в выборе компонентов, необходимых для сборки всего устройства. Робот в разобранном виде изображен на рис. 2.38. В нем использованы шесть двигателей постоянного тока, редукторы, ременные передачи, рельс и тележка. При синтезе основной задачей проектировщика являлась разработка точных моделей компонентов системы и исследование их взаимодействия.
Пример 2.15. Синтез фильтра низких частот
Цель состоит в синтезе низкочастотного фильтра первог о порядка, который пропускал бы сигналы с частотой менее 106.1 Гц и ослаблял сигналы с частотой выше указанной. Кроме того, фильтр должен иметь коэффициент передачи по постоянному току, равный 1/2.
|
Рис. 2.38. Элементы робота ORCA в разобранном виде: 1 — ячеистая платформа, 2 — рельс и тележка, 3 — привод тележки, 4 — шасси, 5 — литой корпус, 6 — привод плеча, 7 — ременные передачи, 8 — крышка предплечья, 9 — литое предплечье, 10 — захват руки в сборке, 11 — литая рука, 12 — локтевое сочленение, 13 — плечевое сочленение, 14 — печатная плата управления корпусом, 15 — печатная плата и двигатели, управляющие локтем и запястьем, 16 — крышка руки |
В качестве искомого фильтра может служить двухзвенная цепь с одним реактивным элементом. изображенная на рис. 2.39(a). Заметим, что эта схема действительно будет иметь требуемый коэффициент передачи, поскольку конденсатор для постоянного тока представляет собой разомкнутую цепь. Выражения для токов и напряжений имеют вид:
/, = (К, - V2)C. h = (Уг ~ Уъ)С>,
У2 = (У, - I2)R,
Уз = AZ
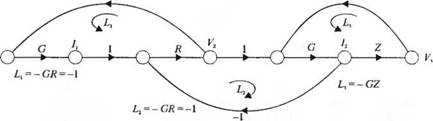
где G = 1/R. Z(s) = 1/Cs и У|(і) = /| (опуская зависимость от і). Эти четыре уравнения отражает сигнальный граф. приведенный на рис. 2.39(6). Граф содержит три контура: L, = - GR = - I. L2 = - GR = -1 и /.j = - GZ. Все контуры касаются прямого пути, а контуры Lt и L3 'не касаются друг друга. Поэтому передаточная функция равна
Т(х)=Уз=___________ !л___________ GZ______ 1 1/ЗДС
1-(А + ^2 + £з)+3+2GZ iRCs+2 S+2/3RG '
-о
|
R
|
|
О- |
+
|
R
|
|
у, к |
С l(s)
|
I |
|
|
|
О |
|
-о |
|
-1 |
|
-1 |
|
Рис. 2.39. (а) Двухзвенная цепь и (б) ее сигнальный граф |
|
і +- |
б)
КО
Заметим, что коэффициент передачи равен 1/2 , как и ожидалось. Желаемое значение полюса р= 2п ■ 106,1 = 666,7 = 2000/3. Отсюда следует, что RC = 0.001. Выберем R = 1 кОм и С = 1 мкФ. Тогда фильтр будет иметь передаточную функцию
|
|