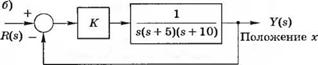СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза с продолжением: система чтения информации с диска
|
□ |
Высококачественные диски имеют до 5000 дорожек на см. Ширина дорожек обычно порядка 1 мкм. Поэтому предъявляются очень жесткие требования к точности позиционирования считывающей головки и к ее перемещению от одной дорожки к другой. В этой главе мы разработаем модель дисковода в переменных состояния, которая будет учитывать эффект изгиба пластины.
Рассмотрим еще раз конструкцию считывающего устройства, изображенную на рис. 2.65. Поскольку для быстрого перемещения головки необходимо иметь малую массу рычага, то нам придется учесть эффект изгиба пластины, изготовленной из очень тонкой упругой стальной ленты. Еще раз отметим, что нам необходимо с высокой точностью управлять положением головки y(t), как это показано на рис. 3.34(g) (шаг 2 процедуры синтеза на рис. 1.19). Прежде всего мы попытаемся разработать модель системы, изображенной на рис. 3.34(a). Обозначим массу двигателя через Мх, а массу головки через М2- Изгиб пластины будем характеризовать коэффициентом упругости к. Сила u(t), приводящая в движение массу Мх, создается двигателем постоянного тока. Если пластина является абсолютно жесткой (не подверженной изгибу), то мы получим упрощенную модель, изображенную на рис. 3.34(6). Типичные параметры этой системы с двумя массами приведены в табл. 3.3.
|
► q(t) !-► y(t) Упругая Масса J Положение пластина головки головки —АШЛЛАЛ— м2 k — |
|
а) |
|
Масса двигателя |
|
y{t) |
|
u(t) - Сила |
|
Mi |
|
u(t) |
|
Ьг |
|
б) |
Рис. 3.34. (а) Модель системы с двумя массами и упругой пластиной.
(б) Упрощенная модель с жесткой пластиной
|
Таблица 3.3. Типичные параметры системы с двумя массами
|
Сначала мы получим передаточную функцию упрощенной модели на рис. 3.34(6) (шаг 5 процедуры синтеза на рис. 1.19). Учтем, что М= Мх+Мг = 20,5 г = 0,0205 кг. Тогда мы имеем:
|
(3.130) |
M^ + bl^- = u(t). dt2 dt
Следовательно, передаточная функция модели
Y(s) 1
U(s) S (Ms + )
С учетом параметров в табл. 3.3 получим:
|
40 |
Y(s)_ 1 _______
U(s) s (0,0205s + 0,410) s (s + 20)'
Структурная схема считывающего устройства с учетом обмотки электродвигателя приведена на рис. 3.35. При R = 1 Ом, L = 1 мГн и Кт = 125 мы имеем:
7(s) 5000
G(s) = -
F(s) s(s+ 20) (s+ 1000)
что совпадает с передаточной функцией, полученной в гл. 2.
(3.131)
Рис. 3.35
Структурная схема считывающего устройства с жесткой пластиной
|
Обмотка двигателя |
U(8) |
Масса |
||
|
Кп |
1 |
|||
|
Ls + R |
Сила |
s(Ms + bj) |
|
F(s) |
|
Y(s) |
Теперь получим модель в переменных состояния для системы с двумя массами, изображенной на рис. 3.34(a). Дифференциальные уравнения имеют следующий вид:
|
dt (fy dt |
для массы Мх М, —^ + ЪХ — + k(q - у) = u(t), dt2
d2 у
для массы М2: М2 —~ + b2 — + к (у - q) = 0.
Выберем в качестве переменных состояния Х = q их2=у. Тогда
dq dy
— И Хл =—.
dt dt
Уравнение состояния в векторно-матричной форме:
х = Ах + В и,
|
(3.132) |
где
|
Я |
0 |
0 |
0 |
1 |
0 |
||
|
у |
0 |
0 |
0 |
0 |
1 |
||
|
> в = |
, А = |
||||||
|
Я |
1/М, |
-к! Мх |
кІМу |
-Ьх 1МХ |
0 |
||
|
_У_ |
0 |
к! М2 |
-к/М2 |
0 |
-ь2/м2 |
|
X = |
Заметим, что выходом является y(t) =х4. Кроме того, пренебрегая индуктивностью обмотки двигателя (L = 0, имеем и(1) = Kniv(t). Выбрав значение к= 10и используя остальные параметры из табл. 3.3, получим:
|
ВТ |
= [0 0 |
50 0] |
|
|
0 |
0 |
1 |
0 ' |
|
0 |
0 |
0 |
1 |
|
-500 |
500 |
-20,5 |
0 |
|
20000 |
-20000 |
0 |
-8,2 |
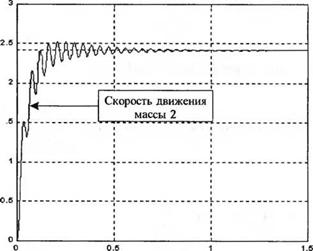
Реакция переменной у при v{t) = 1 В, t > 0 изображена на рис. 3.36. Характер процесса является сильно колебательным, поэтому ясно, что необходимо иметь пластину с большой жесткостью, т. е. выбирать к > 100.
|
Единицы; к — кг/м, b — кг/(м/с) т — кг |
Рис 3.36
Реакция переменной у на ступенчатое входное воздействие в модели с двумя массами при к = 10
% Параметры модели к=10;
М1=0.02; М2=0.0005;
Ы=410е-03; Ь2=4.1е-03:
t=£0:0.001:1.5]; Ч-------
% Модель в переменных состояния А=[0 0 1 0; 0 0 0 1; - К/М1 кУМ1 - Ы/М1 0; кУМ2 - кУМ2 0 -Ь2/М2];
В=[0;0;1/М1;0]; С=[0 0 0 1]; D=[0]; sys=ss(A, B,C. D);
% Вычисление переходной характеристики step(sys. t), grid
xlabel( Время (с)'), уІаЬеІ(‘Скорость (м/с)')
|
Вр[!»Я (С) |
Резюме
В этой главе мы рассмотрели метод описания и анализа систем во временной области. Были введены понятия состояния и переменных состояния системы. Показано, что в качестве переменных состояния целесообразно выбирать такие переменные, которые характеризуют накопление энергии в системе; в то же время было замечено, что набор переменных состояния не является единственным. Рассмотрено дифференциальное уравнение состояния и способы получения его решения (t). Было продемонстрировано, что передаточную функцию (или дифференциальное уравнение) системы можно представить двумя различными конфигурациями сигнального графа. Затем было показано, как по этим сигнальным графам можно легко записать дифференциальное уравнение состояния. Проиллюстрировано применение к сигнальным графам формулы Мейсона и показано, как с ее помощью можно определить переходную матрицу состояния, а с помощью последней — временные характеристики системы. Рассмотрен также дискретный способ получения временных характеристик нелинейных и нестационарных систем. Установлено, что дискретная аппроксимация временных характеристик и переходной матрицы состояния линейных систем хорошо поддается программированию и решению задач на цифровом компьютере. Обсуждено и проиллюстрировано на примерах применение MATLAB для преобразования одного вида модели системы (передаточной функции) в другой (уравнение состояния) и вычисления переходной матрицы состояния. В заключительной части главы была разработана модель в переменных состояния для системы чтения информации с диска.
Упражнения
|
|
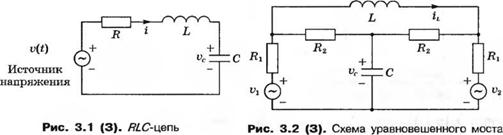
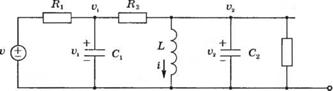
У-3.1. Укажите, что бы вы приняли в качестве переменных состояния для цепи, изображенной на рис. 3.1 (У).
У-3.2. Дифференциальное уравнение, описывающее движение одного сочленения Vl руки робота, имеет вид:
Yt = - *iv(0 - к2><*) + кАЧ ~
Рис. 3.1 (У). RLC-цепь
где v(/) — скорость, y(t) — положение, а »(0 — ток в обмотке двигателя, управляющего сочленением. Запишите уравнения состояния и определите соответствующие матрицы для случая к, = к2 = 1.
У-3.3. Система описывается уравнением состояния (3.16), где
ГО 11
4-і - і ■
Определите корни характеристического уравнения системы.
Ответ', s = -1/2 ± j'JbIZ У-3.4. Получите в переменных состояния описание системы, дифференциальное уравнение которой имеет вид:
d* V d2 у dy
j - + 4 —+ 6^-+ 8у=10и(0. di dt2 dt
У-3.5. На рис. 3.5(У) изображена структурная схема системы. Запишите уравнения состояния для этой системы в форме (3.16) и (3.17).
|
Рис. 3.5 (У). Структурная схема системы |
У-3.6. Система описывается уравнением (3.16), где
О Г
О О
А =
(а) Определите матрицу Ф(г). (б) Определите х(/) при начальных условиях л,(0) =^2(0) = 1. Ответ: (б) = (1 + /), х2 = 1, / > 0.
У-3.7. Рассмотрите систему из пружины и массы, изображенную на рис. 3.3, где М= 1 кг, к= 100 Н/м, Ь = 20Н/м/с.
(а) Запишите векторно-матричное уравнение состояния.
|
Ответ', (а) х = |
(б) Определите корни характеристического уравнения данной системы.
|
0 |
1 ' |
'o' |
|||
|
X = |
-100 |
-20 |
х + |
1 |
и |
|
(б) s = -10, -10. |
У-3.8. Посадка на борт небольшого судна в условиях неблагоприятных погодных условий затруднена из-за качки. Динамика качки описывается матрицей А:
|
"0 |
1 |
0 |
|
|
A = |
0 |
0 |
1 |
|
0 |
-5 |
-2 |
Определите корни характеристического уравнения.
|
ЮМ |
|
*»- *2 |
|
Выходная переменная |
|
Рис. 3.9 (У). ЯС-цепь |
|
|
У-3.9. На рис. 3.9(У) изображена электрическая цепь, находящаяся в режиме свободного движения. В качестве физических переменных состояния выбраны заряды на і Ф конденсаторах, т. е. xl=ql и х2 = д2- (а) Изобразите сигнальный граф с физическими переменными состояния и запишите вектор-
но-матричное дифференциальное уравнение, (б) Перейдите к диагональной (канонической) форме графа и соответствующему дифференциальному уравнению. Учтите, что і, = dqxldt = dxt/dt и i2 = dx2ldt. В качестве выходной переменной примите ток i2.
У-3.10. Система управления посадкой летательного аппарата описывается двумя переменными состояния, и матрица А имеет вид:
_ 0 б'
-1 -5
А =
(а) Вычислите корни характеристического уравнения.
(б) Определите переходную матрицу состояния Ф(/). Ответ: (a) s = -3, -2.
|
-6е"3' + ве2' |
|
(б) Ф(0 = |
|
.„-2/ |
|
Ъе~” - 2-е |
|
Зе~2' - 2е~ е'ъ‘ - ^ |
У-3.11. Составьте описание в форме фазовой переменной для системы, заданной передаточной функцией
Y(s) 4 (s + 3)
R(s) (s+2)(s+4)
У-3.12. Получите модель в переменных состояния для электрической цепи, изображенной на рис. 3.12(У). Определите реакцию цепи на единичное ступенчатое входное воздействие, считая начальные значения тока и напряжения на конденсаторе нулевыми.
|
R = 4 Ом |
|
L = 0.10 Гн |
|
с — юоо мкФ : |
|
Vr |
|
Рис. 3.12 (У). RLC-цепь |
У-3.13. Система описывается двумя дифференциальными уравнениями:
dy
v у — 2и+ aw = 0.
dt
dW L Л Гі
by+ 4 и = О,
dt
где w и у есть функции времени, a u(t) — входное воздействие, (а) Выберите переменные состояния. (б) Запишите матричное дифференциальное уравнение и определите элементы матриц. (в) Определите корни характеристического уравнения системы как функцию параметров а и Ь.
Ответ', (в) s = — 1/2 ± V1 - 4аЪ /2 У-3.14. Опишите в пространстве состояний радиоактивное вещество с массой М, которая пополняется со скоростью r(t) = Ku(t), где К = const. Поясните смысл переменных состояния.

|
I—► X |
q |
||
|
k |
К |
||
|
-чш— |
171 |
—чЛААЛ— |
т |
|
Коэффициент трения скольжения ^ Ь |
|
К HM/VH ihr |
|
kx —МЛЛ-і |
||
|
т1 |
т2 |
|
—7МА— u{t) -* Внешняя сила |
|
. - |
Рис. 3.15 (У). Система с двумя массами Рис. 3.16 (У). Две связанные тележки
У-3.15. Рассмотрите систему с двумя взаимосвязанными массами, изображенную на рис. 3.15(У). Коэффициент трения скольжения каждой массы равен Ь. Запишите векторно-матричное уравнение состояния.
У-3.16. На рис. 3.16(У) изображены две тележки, трением качения которых можно пренебречь. Внешняя сила равна u(t). Выходом является положение тележки 2, т. е. y(t) = g(t). Запишите векторно-матричное уравнение состояния.
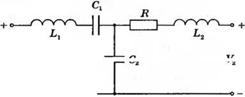
У-3.17. Запишите векторно-матричное дифференциальное уравнение состояния для цепи, представленной на рис. 3.17(У).
У-3.18. Запишите векторно-матричное дифференциальное уравнение состояния для цепи, изображенной на рис. 3.18(У). В качестве переменных состояния примите xt = х2 = i2 nx3 = v.
|
R3 |
Rt
|
Ф”* |
^ф C2=bu2 ©и, фу„
|
Рис. 3.17 (У). RC-цепь |
Рис. 3.18 (У). RLC-цепь
У-3.19. Система с одним входом и одним выходом описывается уравнениями
|
" 0 |
1 ■ |
'о' |
||
|
X = |
х + |
|||
|
-3 |
-4 |
1 |
у=[ 10 0] х.
Определите передаточную функцию G(s) = Y(s)IU(s).
Ответ: G(s) = —z---------- .
s + 4s + З
Задачи
3-3.1. На рис. 3.1(3) изображена RLC-пеиь. (а) Выберите переменные состояния, (б) Запишите систему дифференциальных уравнений первого порядка относительно переменных состояния,
(в) Запишите векторно-матричное уравнение состояния.
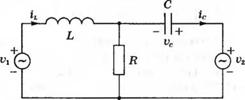
3-3.2. На рис. 3.2(3) изображена схема уравновешенного моста. В качестве переменных состояния примите (хь х2) = (vc, і,), (а) Покажите, что для данной схемы матрицы А и В имеют вид:
|
А = |
-2/(Л, + R2)C |
0 |
, в =-------- і— |
' 1/С |
1/С ' |
|
0 |
-2Л, Л2/(Л| + R2)L |
Rt+ R2 |
r2/l |
-r2/l_ |
|
(б) Изобразите структурную схему в переменных состояния, приняв (х,, х2) = (vc, iL).
|
|
Рис. 3.3 (3). RLC-цепь |
3-3.3. На рис. 3.3(3) изображена электрическая цепь, в которой переменными состояния являются х, = iL и х2 — vc. (а) Получите дифференциальное уравнение состояния.
[О 1/L
Ответ (частично): А =
-1/С -1/ЛС 3-3.4. Система имеет передаточную функцию
r(s)_
R(s) s3 + 2s2 + 3s + 10 '
|
T(s) = |
+ 2s + 5
Изобразите модель системы в виде сигнального графа и запишите векторно-матричное уравнение состояния для двух вариантов конфигурации графа: (а) в форме фазовой переменной и
(б) в виде структуры с многомерным входом.
3-3.5. На рис. 3.5(3) изображена замкнутая система управления, (а) Определите передаточную функцию системы T(s) = Y(s)/R(s). (б) Изобразите сигнальный граф для случая, когда он представлен в форме фазовой переменной, и запишите матричное дифференциальное уравнение состояния. (в) Изобразите сигнальный граф и запишите матричное дифференциальное уравнение состояния относительно физических переменных, указанных на рис. 3.5(3).
3-3.6. Запишите матричное уравнение состояния для электрической цепи, изображенной на рис. 3.6(3). Переменными СОСТОЯНИЯ ЯВЛЯЮТСЯ Х, = V|, Х2= V2 И х3 = І.
|
Рис. 3.5 (3). Замкнутая система управления 4 кОм 2 мГн |
I
|
0.5 мкФ |
:0.25 мкФ v,
Рис. 3.6 (3). /?ІС-цепь
|
R(s) Заданная ~ глубина |
|
Рис. 3.7 (3). Система управления подводным роботом |
3-3.7. На рис. 3.7(3) изображена система автоматического регулирования глубины погружения подводного исследовательского робота. Глубина погружения измеряется датчиком давления. Установленный на корме привод имеет коэффициент передачи К = 1 при вертикальной скорости 25 м/с. Передаточная функция робота
|
Привод |
||||
|
К |
5. |
G(s) |
1 |
|
|
S |
|
Y(s) Глубина |
Датчик
давления
H(s)
|
G(s) = |
1 f
s2+ 1
а передаточная функция датчика в цепи обратной связи H(s) = 2s+ 1.
(а) Запишите уравнение состояния, (б) Определите, является ли система устойчивой.
|
Модуль |
|
Тяга двигателя = к dm/dt |
|
|
3-3.8. На рис. 3.8(3) схематически изображен процесс мягкой посадки лунного модуля. Примите в качестве переменных состояния я, = у, х2 = dy/dt, хъ = т, а в качестве управляющего воздействия и = dm/dt. Гравитационная постоянная Луны обозначена через g. Запищите уравнения состояния для этой системы. Является ли данная модель линейной?
|
Поверхность Луны _______ |
|
Рис. 3.8 (3). Управление посадкой лунного модуля |
3-3.9. В системах управления скоростью часто применяются элементы, принцип действия которых основан на использовании потока жидкости или газа. В таких системах совершенно отсутствуют движущиеся механические части. Они способны поддерживать заданное значение скорости с точностью до 0,5% за счет использования регулируемого ответвления потока и золотникового исполнительного устройства. Такие системы обладают также малой чувствительностью к возмущениям и высокой надежностью в широком диапазоне температур, электромагнитного и ядерного излучения, ускорений и вибрации.
|
О- |
|
»-w(s) Скорость |
|
R(s) - Заданная — скорость |
|
Золотниковое ИУ |
Возмущение А |
|||
|
Фильтр |
Турбина |
|||
|
10 |
1 |
1 |
||
|
(s + 10 ) |
S |
;U |
Js + b |
|
Регулируемое ответвление и детектор ошибки |
|
К, |
|
Рис. 3.9 (3). Система управления паровой турбиной |
Усиление в системе достигается за счет использования форсунки с отклонением потока. Система подобного рода может управлять паровой турбиной мощностью 500 кВт со скоростью 12000 об/мин. Структурная схема такой системы изображена на рис. 3.9(3).
Параметры системы заданы безразмерными единицами: Л = 0,1, ./ = 1 и А', = 0,5. (а) Определите передаточную функцию замкнутой системы 7’(.у) = co(s)/R(s). (б) Запишите векторно-матрич - ное дифференциальное уравнение состояния, (в) Определите характеристическое уравнение системы, использовав для этого матрицу А.
3-3.10. На рис. 3.10(3) изображена двухко
|
Рис. 3.10 (3). Двухкоординатная система управления |
ординатная система управления. Коэффициенты передачи по каналам соответственно равны Кх и К2, а переменные состояния обозначены на рисунке.
(а) Запишите дифференциальное уравнение состояния, (б) Получите характеристическое уравнение системы, использовав для этого матрицу А. (в) Определите переходную матрицу состояния при Кх = 1 и К2 = 2.
3-3.11. Система описывается уравнением (3.16), где
1 -2
Известно, что u(t) = 0, ^(О) =х2(0) = 10. Определите *,(<) и x2(t). 3-3.12. Система описывается передаточной функцией
J» S(s+5)
|
ОД |
s3 + 12s2 + Us + 48 '
(а) Представьте систему в форме фазовой переменной, (б) Определите канонический вид матричного уравнения состояния, (в) Определите переходную матрицу состояния Ф(/).
3-3.13. Рассмотрите еще раз RLC-цепь из задачи 3.1, полагая Л = 2,5, L= 1/4 и С= 1/6.
(а) С помощью матрицы А определите характеристическое уравнение системы и исследуйте ее устойчивость, (б) Определите переходную матрицу состояния цепи, (в) Определите реакцию системы, если начальное значение тока через индуктивность равно 0.1 A. vc.(0) = 0 и v(/) = 0.
(г) Повторите п. (в), если все начальные условия равны нулю, a v(/) = Е = const при t > 0.
3-3.14. Получите векторно-матричное уравнение состояния для системы, имеющей передаточную функцию
т_______________________________
R(s) s3 + 9s2 + 26s + 24
|
п*) = |
s + Is+2
3-3.15. Изобразите сигнальный граф и запишите матричное уравнение состояния для системы с передаточной функцией
гм-М 3(;*6)--------------------------- _
ад s3 + ios2+ 3is+ зо
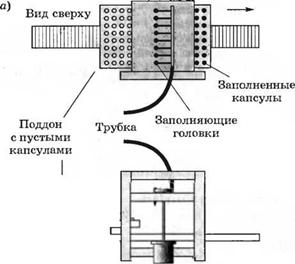
представив ее (а) в форме фазовой переменной и (6) в канонической (диагональной) форме. 3-3.16. На рис. 3.16(3), (а) изображена система распределения в капсулы радиоактивной жидкости. Движение поддона с капсулами в горизонтальном направлении осуществляется с помощью линейного привода. Структурная схема системы управления этим движением приведена на рис. 3.16(3), (б). Полагая К = 500. (а) представьте систему в переменных состояния и (б) вычислите ее реакцию на единичное ступенчатое входное воздействие, (в) Определите корни характеристического уравнения замкнутой системы.
|
Ось х |
|
I Стол I--------- |
|
|
Рис. 3.16 (3)
|
Линейный привод Двигатель Вид сбоку с червячной передачей |
Автоматическое распределительное устройство
|
|
3-3.17. Динамические характеристики подводной лодки существенно отличаются от аналогичных характеристик самолета, ракеты или надводного корабля. Это различие объясняется в первую очередь наличием момента в вертикальной плоскости, возникающего за счет выталкивающей силы. Поэтому представляет интерес рассмотреть задачу управления глубиной погружения подводной лодки. Уравнения, описывающие динамику подводной лодки, можно получить с помощью законов Ньютона из рассмотрения углов, обозначенных на рис. 3.17(3). Чтобы упростить эти уравнения, предположим, что угол 0 является малым, а скорость v постоянна и равна 7, 5 м/с. Рассматривая движение только в вертикальной плоскости, примем в качестве переменных состояния х, = 0, х2 = dQ/dt их3 = а, где а — угол атаки. В этом случае векторно-матричное уравнение состояния имеет вид:
|
0 |
1 |
0 |
0 |
||
|
X = |
-0,0071 |
-0,111 |
0,12 |
х + |
-0,095 |
|
0 |
0.07 |
-0.3 |
0.072 |
|
т |
|
Центр тяжести |
|
|
|
0 Скорость v |
|
Руль глубины |
|
|
|
Рис. 3.17 (3). Управление глубиной погружения подводной лодки |
|
где ll(t) = Ss(t) — отклонение кормового руля глубины. (а) Определите, является ли система устойчивой, (б) Используя дискретную аппроксимацию уравнения состояния, определите реакцию системы на ступенчатое изменение угла 8„ равное 0,285е, считая начальные условия нулевыми. Примите шаг дискретности по времени Т= 2 с. (в) Задав шаг дискретности Т= 0,5 с. с помощью цифрового компьютера вычислите реакцию каждой переменной состояния в течение 80 секунд. Сравните реакции, полученные в пп. (б) и (в). 3-3.18. Система описывается уравнениями состояния: |
|
' 1 |
1 |
-1‘ |
'0' |
||
|
х = |
4 |
3 |
0 |
х + |
0 |
|
-2 |
1 |
10 |
1 |
|
у =[20 30 10] х. |
|
Ч>2 Запястье |
|
МмммМ к, Ъ |
|
»(*) Ток |
|
Определите G(s)= Y(s)/U(s). Рис. 3.19 (3) Фрагмент промышленного робота |
|
Двигатель |
— |
( |
|
|
— |
V |
3-3.19. Рассмотрите задачу управления роботом, схематически представленную на рис. 3.19(3). Двигатель в локтевом сочленении приводит в движение запястье через предплечье, обладающее определенной гибкостью, как показано на рисунке в виде пружины. Пружина имеет коэффициент упругости к и коэффициент трения Ь. Пусть переменными состояния являются •*1 = Фі _ Ч>2 и х2 = Юі-Ч, гДе шо = k(J + Запишите уравнение состояния в вектор
но-матричной форме, ЄСЛИ Х3 = (Uj/COq.
3-3.20. В ряде случаев производную аппроксимируют следующим выражением:
x(t) а [Зх (к + 1) — 4х (к) + х (к -1)].
При такой аппроксимации для оценки производной нужно знать два предшествующих значения сигнала, тогда как при использовании выражения (3.89) — только одно. Используя данную аппроксимацию, повторите вычисления примера 3.6. Сравните значения х,(/)- полученные при Т= 0,2 с, с данными, приведенными в табл. 3.1. Является ли данная аппроксимация более точной?
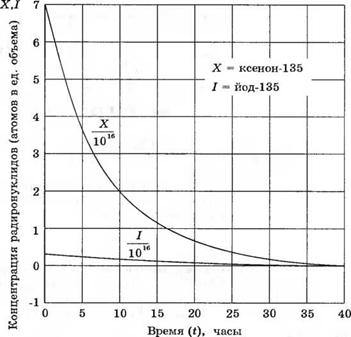
3- 3.21. Яаерный реактор, работавший при постоянном уровне мощности и при высокой плотности потока тепловых нейтронов, внезапно останавливают. В момент остановки плотность ксенона-135 (X) и йода-135 (Г) составляет соответственно 7 ■ 1016 и 3 • 1015 атомов в единице объема.
|
|
|
Рис. 3.21 (3) Характеристики ядерного реактора |
Период полураспада радионуклидов йод-135 и ксенон-135 составляет соответственно 6,7 и 9,2 час. Уравнения распада имеют вид:
|
0,693 6,7 |
|
0,693 9,2 |
|
Л Х=- |
|
X -1. |
Определите концентрации йода-135 и ксенона-135 как функции времени после остановки реактора (а) путем вычисления реакции с помощью переходной матрицы состояния и (6) путем дискретного вычисления этих характеристик. Убедитесь, что реакция системы имеет вид, изображенный на рис. 3.21(3).
|
Ща) |
|
Y(s) |
|
Рис. 3.22 (3). Модель системы второго порядка |
|
|
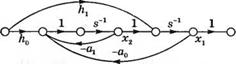
3-3.22. Существует несколько различных эквивалентных способов представления сигнального графа в переменных состояния. Две таких эквивалентных модели, соответствующие передаточной функции (3.38), изображены на рис. 3.8 и 3.10. Еще одна возможная конфигурация сигнального графа приведена на рис. 3.22(3). В данном случае
система имеет второй порядок и ее передаточная функция
G(J) = IW= у±4>_.
U (s) s + + a0
|
и(0ь |
(а) Убедитесь, что граф на рис. 3.22(3) действительно соответствует этой передаточной функции. (б) Покажите, что векторно-матричное дифференциальное уравнение, соответствующее графу, имеет вид:
|
' 0 |
1 ' |
х + |
К |
|
-°о |
""і. |
Л. |
где Л] = i»j и h2-b0-blal.
|
|
|
о + |
|
^ У Выходное 3 “ напряжение |
|
Рис. 3.23 (3). /?/.С-цепь |
3-3.23. Определите вид матричного дифференциального уравнения состояния для электрической цепи, изображенной на рис. 3.23(3). Переменными состояния являются = г, х2 = v, и хъ = v2. Выходная переменная есть v0(/).
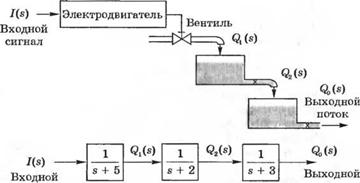
3-3.24. На рис. 3.24(3) изображена система с двумя проточными баками. Электродвигатель изменяет степень открытия входного вентиля и в конечном счете влияет на скорость выходного потока. Система имеет передаточную функцию
T(s) = - ------------------------ ,
s3 + 10s + 31s + 30
а ее структурная схема представлена на рис. 3.24(3), (б). Изобразите сигнальный граф и запишите матричное дифференциальное уравнение состояния для следующих конфигураций графа: (а) в форме фазовой переменной, (б) в виде структуры с многомерным входом, (в) в физических переменных состояния и (г) с развязанными переменными состояния.
|
|
|
о) |
|
поток |
Рис. 3.24 (3)
Система с двумя проточными баками.
(а) Физическая модель и
|
б) |
(б] структурная схема.
3-3.25. Представляется очень заманчивым поддерживать постоянную температуру в здании с помощью регуляторов, использующих накопление солнечной энергии. Одна из таких систем описывается уравнениями:
dx,
—1 = ІХ, + и, + и, ,
dt
dx0
—i + щ + а,
dt
где xt — отклонение температуры от желаемого значения, а х2 — температура среды, накапливающей энергию (например, резервуар, наполненный водой). Соответственно к, и и2 есть тепловые потоки, отдаваемые в окружающую среду и поступающие от источника (Солнца), где транспортной средой является движение воздуха. Возмущение со стороны поступающей солнечной энергии, изменяющее температуру накопителя (например, из-за сплошной облачности), представлено переменной d. Запишите матричное уравнение состояния и определите реакцию системы при и, = 0, «2 = 1 и d= 1 в случае нулевых начальных условий.
3-3.26. Система описывается следующим дифференциальным уравнением:
|
"-I 0" |
'0" |
|
|
х + |
||
|
2 -3 |
1 |
КО-
Определитс матрицы Ф(5) и Ф(/) для данной системы.
|
Рис. 3.27 (3). Система с обратной связью |
3-3.27. На рис. 3.27(3) изображена структурная схема системы. Запишите дифференциальное уравнение состояния и определите переходную матрицу состояния Ф(і’).
|
Рис. 3.28 (3). Гироскоп |
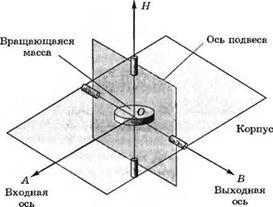
3-3.28. На рис. 3.28(3) изображен гироскоп с одной степенью свободы. Гироскопические датчики измеряют угловое перемещение и используются в системах управления полетом. Ось вращения гироскопа смещается относительно направления ОБ (выходной переменной). Входная переменная есть угловое перемещение относительно оси ОА. Уравнение движения относительно выходной оси получается путем приравнивания скорости изменения угловых моментов сумме действующих моментов. Составьте описание гироскопической системы в переменных состояния.
|
У і |
У- 1 |
||
|
и —► |
т1 |
т2 |
|
|
Сила |
к |
|
Коэффициент трения качения = Ь |
3-3.29. На рис. 3.29(3) изображена система с двумя массами. Коэффициент трения качения равен Ь. Запишите уравнение состояния в матричной форме, если выходная переменная есть y2(t).
|
Рис. 3.29 (3). Система с двумя массами |
3-3.30. В настоящее время значительные усилия направлены на поиск способов манипулирования с объектами в космосе — например, при сборке космической станции или снятии спутника с орбиты. Для выполнения этих задач в грузовом отсеке космического челнока размешается дистанционно управляемый манипулятор. Эффективность использования
такого манипулятора подтверждена последними полетами челноков, но теперь уже рассматривается проект создания нового устройства — манипулятора типа руки с надувными сегментами. Это позволит примерно в четыре раза уменьшить вес манипулятора и в восемь раз — объем, занимаемый им в грузовом отсеке космического челнока.
На рис. 3.30(3), (о) схематически показано применение манипулятора для сборки некоторой конструкции, а на рис. 3.30(3), (6) изображена модель гибкой руки манипулятора, где J— момент инерции приводного двигателя, a L — расстояние до центра тяжести элемента, играющего роль нагрузки. Запишите уравнения состояния для этой системы.
|
Многозвенная рука робота
Манипулятор |
|
б) |
|
|
|
Приводной двигатель |
Космическая
конструкция
|
Рис. 3.30 (3). Дистанционно управляемый манипулятор
|
3-3.31. Получите уравнения состояния для ік
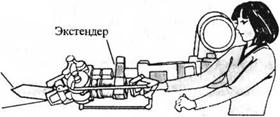
электрической цепи с двумя входами и одним выходом, изображенной на рис. 3.31(3), считая выходной переменной ток i2- 3-3.32. Экстендер — это особый тип манипуляторов, увеличивающий силу человеческой руки при различных дей - Рис. 3.31 (3). RLC-цепь с двумя входами ствиях с нагрузкой, как показано на рис. 3.32(3). Передаточная функция такой системы
М. С(,).-а,
U(s) s2+4s+3
|
|
где U(s) — усилие человеческой руки, прикладываемое к манипулятору, a Y(s) — усилие, прикладываемое манипулятором к нагрузке. Взяв за образец структуру графа на рис. 3.7, т. е. использовав его представление в форме фазовой переменной, запишите уравнения состояния и определите переходную матрицу состояния.
Рис. 3.32 (3)
Экстендер, увеличивающий силу человеческой руки
Нагрузка
Захват
3-3.33. Лекарство, принимаемое внутрь, усваивается со скоростью г. Масса лекарства, находящегося в желудочно-кишечном тракте, равна ть а масса лекарства в кровеносной системе — т2. Скорость изменения массы лекарства в желудочно-кишечном тракте равна разности скоростей его усвоения и поступления в кровеносную систему, причем считается, что она пропорциональна текущему значению массы. Скорость изменения массы лекарства в кровеносной системе пропорциональна его количеству, поступающему из желудочно-кишечного трата минус скорость, с которой масса теряется за счет метаболизма, которая пропорциональна текущему значению массы лекарства в крови. Разработайте модель этой системы в переменных состояния.
Для частного случая, когда элементы матрицы А равны единице (с соответствующими знаками), определите реакцию системы на начальные условия т,(0) = 1 и т2(0) = 0. Постройте график изменения переменных состояния в зависимости от времени, а также соответствующую траекторию на плоскости (дг|, х2).
3-3.34. Динамика ракеты описывается передаточной функцией
^-gw-4.
U(s) s
причем используется обратная связь по состоянию и = - х2 - 0,5х|; где jcj =>'(/) и х2 = y{t). Определите корни характеристического уравнения системы и ее реакцию на начальные условия jc, (0) = 0 и х2(0) — 1. U(s) и Y(s) соответствуют приложенному моменту и положению ракеты.
3-3.35. Система имеет передаточную функцию
|
Г(«) т |
8
= T(s) =
у3 + Is + 14s + 8
(а) Запишите матричное дифференциальное уравнение состояния для данной системы.
(б) Определите элемент <р,,(/) переходной матрицы состояния.
3-3.36. Изобразите сигнальный граф в переменных состояния для системы, изображенной на рис. 3.36(3). Индуктивностью обмотки двигателя и трением можно пренебречь. Постоянная двигателя Кт = 10, а коэффициент противоЭДС Къ = 0,0706. Момент инерции двигателя и вентиля J= 0,006, а площадь сечения бака равна 50 м*. Учтите, что двигатель управляется током якоря i„. Переменные состояния хj = А. х2 = 0 и - х3 - dO/dt. Считайте также, что расход д, = 800. где 0 — угол поворота вала двигателя. Расход на выходе из бака q0 = 50h(t).
|
Рис. 3.36 (3) Система с проточным баком |
|
Резервуар |
|
|
|
Усилитель Ка =50 |
|
* |
|
=* Вентиль Qi |
Яо
Ж
Задачи повышенной сложности
П-3.1. Рассмотрите систему электромагнитной подвески, изображенную на рис. 3.1(П). В верхней части экспериментальной установки находится электромагнит. С помощью электромагнитной силы/необходимо удерживать стальной шарик в подвешенном состоянии. Заметим, что такая простейшая система является неработоспособной, поэтому требуется использовать обратную связь. Для этого под шариком помешается датчик, измеряющий величину зазора по значению наведенного в нем вихревого тока
Предположим, что в качестве переменных состояния выбраны х, =х. х2 = dx/dt их3 = і. Катушка электромагнита имеет индуктивность L = 0,508 Гн и сопротивление R = 23.2 Ом. Для определения электромагнитной силы используйте разложение в ряд Тейлора. Ток »,=/(, + /. где 10 = 1,06 А соответствует рабочей точке, а і есть величина переменная. Масса шарика т = 1,75 кг. Величина зазора xg=X0 + х, где рабочей точке соответствует Х0 = 4,36 мм, а х есть
малое отклонение. Электромагнитная сила опреде
|
|
|
Электромагнит |
|
f |
f=k(it/xg)2, где к = 2,9-10 4 Н • м2/А2. Запишите матричное дифференциальное уравнение и определите передаточную функцию X(s)/V(s).
П-3.2. Рассмотрите массу т, установленную на тележке, как показано на рис. 3.2(П). Определите передаточную функцию Y(s)/U(s) и на ее основании запишите матричное дифференциальное уравнение состояния.
|
Рис. 3.1 (П). Система электромагнитной подвески |
|
Стальной шарик |
|
|
ляется уравнением
|
Масса т а ~о |
—чЛАЛЛААЛ—
|
mg Датчик зазора |
-Di-
Рис. 3.2 (П). Масса на тележке
|
Транспортное |
|
|
средство |
|
|
1 |
Y(s) |
|
(s + l)(s + 2) |
Положение |
|
Регулятор |
|
|
R(s) |
2 s2+ 6s + 5 |
|
Вход |
s +1 |
П-3.3. Движение автономного транспортного средства из одного пункта в другой требует управления его положением с высокой точностью.
|
Рис. 3.3 (П). Система управления положением |
Подобную задачу решает система, изображенная на рис. З. З(П). Определите каноническую диагональную форму матричного дифференциального уравнения (или приблизьтесь к такой форме по возможности точнее).
|
Рис. 3.4 (П). Модель амортизатора |
П-3.4. В горных велосипедах применяется пружинная амортизация передней вилки. По сравнению с жесткой вилкой, с помощью которой переднее колесо крепится к раме, такая подвеска поглощает ударные импульсы, защищая раму и велосипедиста от тряски. Однако в подобных амортизаторах используется только одна пружина, которая совершенно одинаково реагирует на ударные воздействия как при больших, так и при малых скоростях, хотя эти воздействия значительно отличаются по силе.
Очень хорошим решением является амортизатор с несколькими упругими элементами, которые могут настраиваться во время движения велосипеда. Существуют модели, у которых амортизатор имеет две пружины — одну обычную и вторую в сочетании с масляным демпфером. Такой амортизатор позволяет регулиро-
вать коэффициент упругости, приспосабливая его к профилю
грассы и весу велосипедиста. На рис. 3.4(П) показана схема такой подвески, где параметр b является настраиваемым. Выберите соответствующее значение Ь, позволяющее велосипеду приспосабливаться (а) к сильным ударам при больших скоростях и (б) к слабым ударам при малых скоростях. Примите значения kt = 1 и к2 = 2.
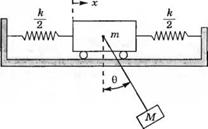
П-3.5. На рис. 3.5(П) изображена масса Л/, подвешенная к другой массе т с помощью легкого стержня длиной L. Считая угол 0 малым, т. е. используя линейную модель системы, запишите матричное дифференциальное уравнение состояния.
|
|
|
Рис. |
|
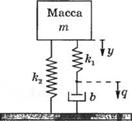
3.5 (П). Масса, подвешенная к тележке |
|
|
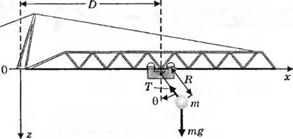
П-3.6. На рис. 3.6(П) изображен подъемный кран, тележка которого перемещается в направлении х, тогда как груз массой т смещается в направлении z. Двигатели, осуществляющие эти перемещения, являются достаточно мощными по отношению к массе тележки, подъемного троса и груза. В качестве входных управляющих переменных рассмотрите расстояния D и R. Примите также, что 0 <50°. Разработайте линейную модель системы и запишите дифференциальное уравнение состояния.
Рис. 3.6 (П)
Подъемный кран с горизонтальным перемещением тележки и вертикальным перемещением груза
Задачи на синтез систем
СС-3.1. Вернитесь к линейному приводу с барабаном и рейкой, изображенному на рис. 2.1(СС). Пренебрегая индуктивностью обмотки двигателя и трением скользящей части стола, получите модель системы в переменных состояния. Параметры системы приведены в табл. 2.1(СС).
С-3.1. Система «масса-пружина» с затуханием, изображенная на рис. 3.3, используется в качестве амортизатора в мотоциклах высокого класса. Заданы следующие параметры системы: те = 1 кг. Ъ = 9 Н ■ с/м, к = 20 Н/м. (а) Определите матричное уравнение состояния системы, корни характеристического уравнения и переходную матрицу состояния Ф(/)- Примите следующие начальные условия: у(0) = [ и dy/dt, _ 0 = 2. (б) Изобразите графически процессы у(е) и dy/dt для первых двух секунд, (в) Измените коэффициент упругости пружины и коэффициент грения таким образом, чтобы уменьшить величину ускорения d~y/dr. действующего на мотоциклиста. Масса при этом должна оставаться постоянной и равной 1 кг.
|
«(/). |
С-3.2. Система описывается следующим уравнением состояния в форме фазовой переменной:
|
' 0 Г |
0' |
|
|
х + |
||
|
-а - Ъ |
d |
|
X = |
|
'-3 |
o' |
т |
||
|
z = |
2 + |
|||
|
0 |
-1 |
1 |
Выходная переменная у= 10*,. Необходимо записать уравнение состояния в канонической диагональной форме:
и, у = [-5 5] z.
Определите параметры а, Ъ и d, при которых уравнение будет иметь требуемый вид.
|
Масса поршня поглотителя энергии т3 = 5 |
|
кг Масса подвижной к каретки nt2= 10 |
|
dx/dt= 60 м/с при х = 0, / = 0. h - 30 м |
|
Коэффициент упругости троса 2 к2 = 1000 |
|
Коэффициент упругости троса 1 Лі = 500 |
|
Масса самолета пц = 300 |
|
лг3(0) = лг2(0) = лг,(0) = 0 |
|
|
|
-VvWv- |
I—vWW—
|
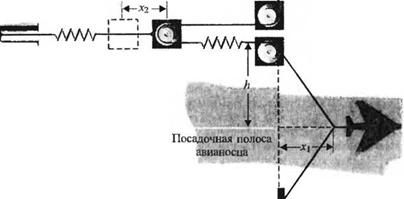
Рис. 3.3 (С). Система остановки самолета на палубе авианосца С-3.3. На рис. 3.3(C) изображена система остановки самолета при его посадке на палубу авианосца. Линейная модель каждого поглотителя энергии обладает тормозящей силой fD = КГ)х3. Необходимо, чтобы самолет останавливался через 30 м после захвата им удерживающего троса. В момент посадки скорость самолета равна 60 м/с. Выберите требуемое значение коэффициента KD и изобразите график изменения переменных состояния. С-3.4. Компания, производящая спортивное оборудование, заказывает вам проектирование корда для прыжков, при котором прыгун не мог бы удариться о землю, если его масса находится в диапазоне от 50 до 100 кг. Дополнительное требование сводится к тому, чтобы время прыжка (т. е. движение вверх и вниз) составляло от 25 до 40 секунд. Определите характеристики корда, считая, что прыгун стоит на платформе в 90 м над землей, а корд прикреплен к перекладине, находящейся в 10 м над платформой. Считайте, что рост прыгуна равен 2 м, а корд пристегнут к поясу (т. е. в точности на уровне 1 м). КО Задачи, решаемые с помощью MATLAB |
|
М-3.1. С помощью функции SS получите модель в переменных состояния для систем, имеющих в разомкнутом состоянии следующие передаточные функции: |
|
3^ +105+1 |
|
1 |
|
s+ 14 |
|
(a )G(s)=- |
|
(б)С(*) = |
|
(в) G(s) = |
|
s3 + 3s2 + Зі + 1 |
|
s + 10............................. + 8s + 5 М-3.2. С помощью функции tf определите передаточные функции для систем, модели которых в пе- ременных состояния представлены следующими матрицами: |
|
' 1 |
1 |
0' |
'0' |
|
|
-2 |
0 |
4 |
, В = |
0 |
|
6 |
2 |
Ю |
1 |
|
С = [1 0]; (б) А = |
|
(а) А = |
|
, В = |
|
0 1 -1 -2 |
|
(в) А = |
|
,С = [1 1]. |
|
,В = |
М-3.3. Рассмотрите схему, изображенную на рис. З. З(М). Считая операционный усилитель идеальным, определите передаточную функцию
|
|
У&УУ,(*).
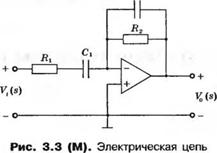
(а) Представьте схему в переменных состояния, если /?| = 1 кОм, /?2 = 10 кОм, С| = 0,5 мФ и С2 = 0,1 мФ. (б) На основании модели в переменных состояния из п. (а) с помощью функции step получите график переходной характеристики.
М-3.4. Рассмотрите систему, заданную уравнениями
|
■ 0 |
1 |
0' |
"O' |
|
|
0 |
0 |
1 |
х + |
0 |
|
-3 |
-2 |
-5 |
1 |
|
и, у=[ 1 0 0] х. |
(а) С помощью функции tf определите передаточную функцию Y(s)/U(s).
(б) Постройте график реакции системы на начальные условия х(0) = [0 —1 I]1 для 0 < t < 10.
(в) С помощью функции ехрт вычислите переходную матрицу состояния и определите х(0 при t= 10 для начальных условий из п. (б). Сравните полученный результат с данными из п. (б).
|
(1) |
|
(2) |
М-3.5. Рассмотрите две системы:
|
' 0 |
1 |
O' |
"O' |
|
|
0 |
0 |
1 |
x, + |
0 |
|
-4 |
5 |
-8 |
_4_ |
|
ц ГІ1 0 0] х, |
|
' 0,5000 0.5000 |
0,7071' |
"0" |
||
|
x2 = |
-0,5000 -0.5000 |
0,7071 |
x2 + |
0 |
|
-6,3640 -0,7071 |
-8,0000 |
4 |
|
и. >-=[0,7071 -0.7071 0]х2. |
(а) С помощью функции tf определите передаточную функцию Y(s)/U(s) для системы (1).
(б) Проделайте то же самое для системы (2).
(в) Сравните результаты пп. (а) и (б) и прокомментируйте их.
М-3.6. Рассмотрите замкнутую систему, представленную на рис. 3.6(М).
(а) С помощью MATLAB получите модель в переменных состояния для регулятора.
(б) Проделайте то же самое для объекта.
(в) Используя результата пп. (а) и (б), с помощью функций series и feedback получите модель в переменных состояния для замкнутой системы и постройте график ее реакции на импульсное входное воздействие.
|
[1 Of. |
М-3.7. Рассмотрите систему
|
" 0 1' |
'O' |
|
|
x + |
||
|
-2 -3 |
1 |
|
и, у=[ 1 0] х |
|
Рис. 3.6 (М) Замкнутая система управления |
|
Щ8) |
|
Л r |
Регулятор |
Объект |
|||
|
1 |
1 |
||||
|
J * |
s + 2 |
sz + 2s + 4 |
|||
|
Y(s) |
при начальных условиях х(0) =
С помощью функции Isim вычислите и изобразите графически реакцию переменных *,(/) и x2(t) при u(t) = 0.
Ключевые термины и понятия
Вектор СОСТОЯНИЯ. Вектор, компонентами которого ЯВЛЯЮТСЯ все п переменных СОСТОЯНИЯ, Х|, Х2, ...,Хп.
Временная область. Математическая область, в которой описание системы задается функциями времени t.
Дискретная аппроксимация. Аппроксимация, используемая для вычисления временных характеристик системы путем деления интервала времени на малые отрезки At.
Дифференциальное уравнение состояния. Дифференциальное уравнение относительно вектора состояния: х = Ах + Ви.
Нестационарная система. Система, в которой один или несколько параметров могут зависеть от времени.
Обратная связь по состоянию. Способ формирования сигнала, прикладываемого к объекту управления, при котором он является непосредственной функцией всех переменных состояния.
Переменные состояния. Совокупность переменных, полностью описывающих поведение системы.
Переходная матрица состояния Ф(0- Матричная экспоненциальная функция, описывающая свободное движение системы.
Состояние системы. Совокупность таких чисел, которые при известных входной функции и уравнениях динамики системы позволяют определить будущее состояние системы.
Фундаментальная матрица. См. переходная матрица состояния.