СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза: ременный привод печатающего устройства принтера
В обыкновенном недорогом принтере для компьютера горизонтальное перемещение печатающего устройства вдоль страницы осуществляется с помощью ременного привода. Печатающее устройство может быть струйным, матричным или термическим. Пример ременного привода принтера с исполнительным устройством в виде двигателя постоянного тока изображен на рис. 3.24. В данной конструкции положение печатающего устройства измеряется с помощью фотодатчика, а натяжение ремня изменяет его коэффициент упругости. Целью синтеза является выбор надлежащих параметров электродвигателя, шкива, регулятора и анализ влияния коэффициента упругости ремня на характеристики системы. Для решения поставленной задачи сначала нам потребуется разработать модель привода и выбрать многие из его параметров. На основании этой модели мы построим сигнальный граф и выберем переменные состояния. После этого определим передаточную функцию системы и выберем ее остальные параметры, кроме коэффициента упругости ремня. И, наконец, исследуем влияние коэффициента упругости, проварьировав его в разумных пределах.
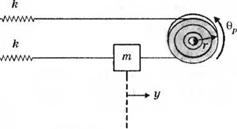
На рис. 3.25 изображена модель ременного привода. Предполагается, что коэффициент упругости ремня равен к, радиус шкива — г, угол поворота вала двигателя — 0, угол поворота правого шкива — вр, масса печатающего устройства — т, а его положение — y(t). Выходом фотодатчика является напряжение vlt пропорциональное перемещению у, т. е. V] = ку. Регулятор вырабатывает выходное напряжение v2, являющееся функцией v,. Напряжение v2 подается на обмотку возбуждения двигателя. Предположим, что мы можем использовать линейную зависимость
|
dt |
и выберем параметры к2 = 0,1 и къ = 0 (т. е. будем использовать обратную связь по скорости).
|
|
|
Рис. 3.24 Ременный привод |
|
Напряжение |
|
fv Ремень 2_ |
|
Источник света |
|
|
|
принтера |
|
Печатающее устройство |
|
К Двигатель F j постоянного | тока |
|
Фото датчик |
|
Регулятор + |
|
y(t) Положение 4— печатающего устройства |
|
Шкив |
|
|
|
- ^ |
Регулятор, dvt |
Датчик |
«........ |
|
|
V2 |
V1 |
У |
|
Двигатель |
|
Рис. 3.25 Модель ременного привода принтера |
|
|
Момент инерции двигателя вместе со шкивом J=Jm + JmK. Если мы выберем двигатель средней мощности в 1/8 л. с. (чуть менее 100 Вт), то для него J = 0,01 кг м2, индуктивностью обмотки возбуждения можно пренебречь, сопротивление обмотки возбуждения равно 2 Ом, постоянная двигателя Кт = 2 Н-м/А, а коэффициент трения совместно со шкивом b = 0,25 Н мс/рад. Радиус шкива г = 0,15 м. Все эти параметры сведены в табл. 3.2.
|
Таблица 3.2. Параметры устройств принтера
|
Перейдем к записи уравнений движения системы; заметим, что у = гвр. Тогда сила натяжения Ту равна:
Г, = А(г0 - г0р) = k{rQ - у).
Сила натяжения Т2 - к(у - г0). Сила, действующая на массу m:
|
£I dt2 |
|
(3.115) |
7J - T2=m
T —T2 = k(rQ-y)-k(y-rQ)=2k(rB-y) = 2kxl, (3.116)
где X[ = (/-0 - у) примем за первую переменную состояния. Пусть второй переменной состояния будет х2 = dy/dt, тогда из (3.115) и (3.116) мы получим:
|
(3.117) |
dx2 _ 2к dt m 1
|
dx, dd =r— |
Если в качестве третьей переменной состояния выбрать х3 = dQ/dt, то
|
dt |
|
dt dt |
dy
Теперь нам потребуется дифференциальное уравнение, описывающее вращение электродвигателя. При L = О ток возбуждения і = v-,/R и момент на валу Тт = Kmi. Следовательно,
Т i-v " R 2’
т. е. момент, развиваемый двигателем, должен быть равен моменту, обеспечивающему движение ремня, плюс возмущающий момент нагрузки:
T„, = T+Td.
Момент Т обуславливает вращение шкива, поэтому
d2Q, Л
T=J^- + b-^ + r(Tl - Г,> dt dt
Таким образом, мы замечаем, что
dx3 d2B dt ~ dt2 ’
из чего следует:
|
2 kr -xl, |
ф3 J'm dt
где
:——v-> и v, =-k, k-y — =-k, k1x1. R ' ' dt
|
В результате мы получаем: |
|
dt JR J J J ' J Уравнения (3.117—3.119) полностью описывают динамику нашей системы. Дифференциа- льное уравнение состояния в векторно-матричном виде таково: |
|
0 |
-1 |
г |
Г -1 |
|
|
0 |
||||
|
2 к |
||||
|
0 |
0 |
х + |
0 |
|
|
m |
1 |
|||
|
2 кг |
Kmklk2 |
Ь |
J |
|
|
_ J |
JR |
J. |
|
X - |
|
Td- |
|
X-, x3 X|------------------------------ |
|
2 kr |
|
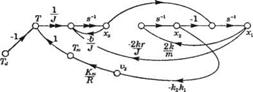
Сигнальный граф, соответствующий этому уравнению, изображен на рис. 3.26, где дополнительно включен узел, отражающий наличие возмущающего момента Td. По графу мы теперь можем определить передаточную функцию Xx(s)IT,^s). По этой передаточной функции легко можно будет установить, как уменьшить влияние возмущения Td на характеристики системы. С помощью формулы Мейсона находим: Г _7 S J |
|
Х(Д)__________ Та (s) I - C^i + l2 + + La ) + L| l2 |
|
Рис. 3.26 Сигнальный граф для ременного привода принтера |
|
Td |
|
(3.119) |
|
(3.120) |
|
|
L, L7=- — s-2, L3=-^-s- Д, =- 2кК”‘к'к2 s~
J т J mJR
Следовательно,
Tj(s) з (2к 2кг "l (2kb 2kKmkxk2r
V J J m J ^ Jm JmR
|
(3.121) |
С учетом численных значений параметров из табл. 3.2 получим: *,(s)_ -15s
Td (s) s3 + 25s2 + 14,5As + 1000* (0,25 + 0,15/c,)
Нам желательно иметь такой коэффициент упругости к и коэффициент регулятора к2, при которых переменная состояния х1 как можно быстрее принимала бы малое значение после появления возмущения. Для проверки примем возмущение в виде ступенчатой функции, т. е. T/s) = a/s. Имея в виду, что х, = г9 - у, упомянутое выше требование эквивалентно тому, чтобы переменная у стала практически равной заданному значению г0. Если ремень является абсолютно жестким, т. е. к -» оэ, то у в точности будет равно гв. При ступенчатом возмущении Tjs) = a/s мы имеем:
Лі(*) = -7 ; — (3-122)
s + 25s2 + 14,5/и + 1000* (0,25 + 0,15к2 )
По теореме о конечном значении
limx1(/) = limsA'1(s) = 0, (3.123)
t—>00 А’—>0
т. е. установившееся значение Xj(t) будет равно нулю. Зададимся реалистичным значением к в диапазоне <к< 40. Пусть это будет 20. Тогда при к2 = 0,1 мы получим:
. — 15а 15а, _ .
Jfi(s) = — = ------------------------- . (3.124)
s3 + 25s + 290s + 5300 (s + 22,56) (s2 + 2,44s + 234,93)
Характеристическое уравнение имеет один вещественный и два комплексных корня. Разложение Xt(s) на простые дроби дает:
Jf,(s) A Rs + С
(3.125)
a s + 22,56 (s+1,22)2 +(15,28)2
где вычисление неопределенных коэффициентов приводит к результатам: А =-0,0218, В = 0,0218, С — —0,43 81. Очевидно, что при таких малых значениях вычетов реакция системы на единичное возмущение будет незначительной. Так как А и В существенно меньше, чем С, TOvV'i(s) можно аппроксимировать выражением:
Jf,(s) -0,4381
• ~ -
a (s+1,22)2 +(15,28)2 Найдем оригинал этого выражения, воспользовавшись табл. 2.3:
»- 0,0287е-1-22' sin 15,28Л (3.126)
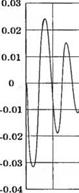
Рис. 3.27
|
|
|
*;(*) |
Реакция переменной ^(t) на ступенчатое возмущение: максимальное значение = - 0,0325
О 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Время (с)
График этой функции приведен на рис. 3.27, откуда следует, что влияние нежелательного возмущения является весьма незначительным. Таким образом, поставленная задача синтеза нами выполнена.