СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Передаточные функции линейных систем
Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные условия равны нулю. Передаточная функция системы (или элемента) однозначно описывает динамическую связь между этими переменными.
Передаточная функция существует только для линейных стационарных (с постоянными параметрами) систем. В нестационарных системах один или несколько параметров зависят от времени, поэтому преобразованием Лапласа воспользоваться нельзя. Передаточная функция описывает поведение системы в терминах вход-выход и не несет никакой информации о внутренних переменных и характере их изменения.
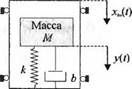
Передаточная функция системы масса-пружина получается, если в исходном уравнении (2.19) все начальные условия положить равными нулю:
|
(2.38) |
Mv2K(.v) + bsY(s) + kY(s) = R(s). Отсюда находим передаточную функцию:
|
(2.39) |
выход. K(.v) 1
= G(s) = —-= ---------------------
вход R(s) Ms2 +bx+k
|
|
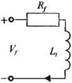
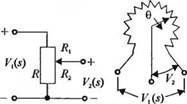
Передаточная функция ЛС-цепи, изображенной на рис. 2.13, получается путем записи в операторной форме уравнений Кирхгофа относительно напряжений:
(2.40)
и далее
|
(2.41) |
|
R
Рис. 2.13. /7С-цепь |
К2(*) = /(*)і-.
Выражая I(s) из (2.40) и подставляя его в (2.41), получим:
|
|
Тогда передаточная функция будет иметь вид:
G(s) = ^^=—-—= - J_=_^L., (2.42)
F[(5) flCs+l ts+1 5+1/т
где т = RC есть постоянная времени цепи. Единственный полюс функции G(s) равен s = - 1/т. Выражение (2.42) можно было бы получить сразу, если рассматривать цепь как обычный делитель напряжения, т. е.
Ут№ = —^(f)— (2 43)
F,(s) Z,(.v)+Z2(.v)
где Z,(.v) = Л, Z2(.v) = 1/Су.
Многоконтурная электрическая цепь или подобная ей механическая система с неско - gm. лькими массами описываются системой уравнений относительно переменной пре - образования Лапласа. Решать такие уравнения обычно удобнее с помощью матриц и определителей. С матрицами и определителями можно познакомиться на Web-сайте MCS.
Теперь рассмотрим поведение системы высокого порядка и найдем ее реакцию на входной сигнал после затухания собственного (свободного) движения. Пусть дифференциальное уравнение системы имеет вид:
т/7 ,, 1/1-1 ІЛ-1 _ 1П-2
“ У « у а г а г /п...
<2 44)
где j>(t) есть реакция системы, a r(t) — входной сигнал, т. е. возмущающая функция. Если все начальные условия равны нулю, то вход и выход системы можно связать передаточной функцией:
У(Д)=С(л-)Д(Д)=^/г(Д)= ‘ +Р"-^П 2+-+Ро R(S). (2.45)
cj(s) s + q„_S +...+qQ
Реакция системы состоит из свободного движения (определяемого начальными условиями) и вынужденного движения, обусловленного входным сигналом. В результате можно записать:
W
Ф) Ф)
где q(s) = 0 есть характеристическое уравнение системы. Если изображение по Лапласу входного сигнала представляет собой дробно-рациональную функцию
d(s)
ТО
У(Ю ==^ ^= Yx (s)+ Y2 (s)+ r3 (s), (2.46)
q(s) q(s) d(s)
где K|(.v)— составляющая, характеризующая свободное движение, У2(5) — составляющая, обусловленная сомножителями q(s), а У3(у) — составляющая, включающая в себя сомножители d(s).
Обратное преобразование Лапласа дает:
АО = УМ + УїС) + Уг( /)•
Переходный процесс в системе обусловлен составляющими}^?) +y2(t), a y^fjt) есть установившееся движение системы.
Пример 2.2. Решение дифференциального уравнения
Рассмотрим систему, описываемую дифференциальным уравнением
d2y. dy „ „ , „
— +4 — + 3y=2r(t)
dt
<Г
dy
|
= 0 при r(t) = 1, / > 0. |
с начальными условиями >’(0) = 1. —
dt
Преобразуя это уравнение по Лапласу, получим:
[ґВД - ч<0)] + 4[вВД ->'(0)] + ЗВД = 2R{s). Поскольку /?(.у) = - и _>j(0) = 1, то
■У
s+ 4
Y(s) =
s2+4s+3 s(s2+4s+3)’
где q(s) = s'+ 4s + 3 = (s + 1 )(s + 3) = 0 есть характеристическое уравнение, a d(s) = s. Tогда разложение У(х) на простые дроби дает:
|
" 3/2 |
J/2.L |
Г 1/3 |
1 |
|
_s+ 1 |
s+з] |
Ь+з |
s+ 1- |
|
Y(S) = |
|
2/3 +-------- =------- Y](s)+Y2(s)+Yi(s). s |
|
гз 1 -3,1 |
1 -3/ -/ |
|
|
— е —е _ 2 2 |
+ |
—і 1 Си 1 гп 1 |
Следовательно, реакция системы описывается уравнением:
2 3
а в установившемся режиме lim ylt) = — .
/->® 3
Пример 2.3. Передаточная функция операционного усилителя
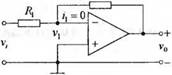
Операционный усилитель (ОУ) относится к важному классу аналоговых интегральных схем, обычно используемых в качестве элементов систем управления и во многих других устройствах. Операционные усилители являются активными элементами (т. е. они имеют внешний источник питания) с высоким коэффициентом усиления при работе в линейном режиме. Модель идеального операционного усилителя приведена на рис. 2.14.
Для идеального ОУ характерным является следующий режим работы: (1) /, = i2 = 0, что соответствует бесконечному входному сопротивлению, И (2) v2 - V, = 0 (т. е. v2 = V|). Связь между входом и выходом идеального ОУ определяется соотношением:
v0 = K(v2 - v,) = - A'(v, - v2),
где К —> то. В данном примере мы будем считать, что имеем дело с идеальным ОУ, работающим в линейном режиме.
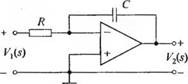
Рассмотрим инвертирующий усилитель, изображенный на рис. 2.15. При указанных выше условиях можно считать, что ix = 0, и для данной схемы справедливо соотношение
■ = Q
|
R, |
R,
|
'|=°. |
|
Инвертирующий вход 4 |
|
о Выход |
|
Неинвертируюший0 вход 4 |
|
Рис. 2.14 Идеальный операционный усилитель |
Так как v, = v, (см. рис. 2.14) и v2 = 0 (см. рис. 2.15), отсюда следует Vj = 0. Таким образом,
|
Рис. 2.15. Идеальный инвертирующий операционный усилитель |
Vi v„
0,
Л, Г<2
откуда имеем
^ _ _^2 V, R,
Если принять /?, = R2, то данная схема просто инвертирует знак входного напряжения.
Пример 2.4. Передаточная функция системы
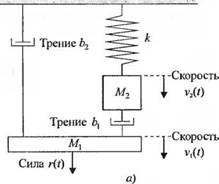
Рассмотрим механическую систему, изображенную на рис. 2.16(c) и ее аналог в виде электрической цепи на рис. 2.16(6). Как было показано в табл. 2.1, сквозными переменными-аналогами в механической и электрической схемах являются, соответственно, сила и ток. Скорости V[(/) и v2(/) механической системы являются прямыми аналогами напряжений v,(/) и v2(0 в электрической цепи. Уравнения, описывающие движение механической системы, в случае нулевых начальных условий имеют вид:
MisVi(s) + (fc, + b2)V,(s) - b, V2(s) = R(s), (2.47)
|
V2(S) _ |
|
(2.48) |
|
0. |
|
M2sV2{s)+b&y2{s)-Vx(s)+k |
Эти уравнения получены на основании сложения сил, действующих на элементы механической системы. Перегруппируя члены, входящие в (2.47) и (2.48), получим:
[Mxs + (Ь, + Ь2)]У^) - b, F2(s) = R(s),
-by{{s) + ^M2s + + — j V2(s) = 0,
|
(2.49) |
или то же самое в матричной форме:
|
Mxs + і) + bj |
-h к |
'W |
'R{s) |
|
|
-h |
M2s + + — s _ |
J2(s) |
0 |
|
v,(0 |
/?, V2 |
(0 |
|
|
r- |
= c, |
J Ro C2- |
|
|
|
|
Ток і ко |
б)
Рис. 2.16. (а) Механическая система с двумя массами;
(б) Электрическая цепь с двумя узлами — аналог механической системы. Параметры-аналоги: С) = Мл, С-г = Mi, L - 1 /к, /?1 = 1 jb, /?2 = /Ь2
Считая выходной переменной скорость массы Л/,, с помощью обращения матрицы либо по правилу Крамера получим:
т =-------------- (M2s + bl + kls)R(s) (250)
(M{s + і) + b2)(M2s + bj + kh)- fc.
Тогда передаточная функция механической (или электрической) системы будет равна:
G(s) = ii^ =_________ (M2s+ + к Is) =_______ (M2s2 + t^s + к)_______
R(s) (Mts+ + b2)(M2s+ + k/s)-bf (M^+bj+b2)(M2s2 + b^+k)-l^s
Если за выходную переменную принять перемещение jc,(/), то передаточная функция примет вид:
|
(2.52) |
ЛГ](я) КДя) _ G(s)
R(s) sR(s) s
В качестве еще одного примера получим передаточную функцию очень важного элемента электрических систем управления — двигателя постоянного тока. Подобные двигатели используются для перемещения нагрузки и носят название исполнительных устройств.
Исполнительное устройство — это элемент системы управления, обеспечивающий поступление на вход объекта управления сигнала достаточной мощности.
Пример 2.5. Передаточная функция двигателя постоянного тока
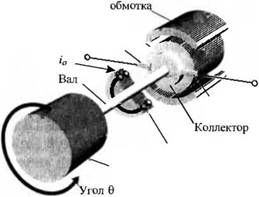
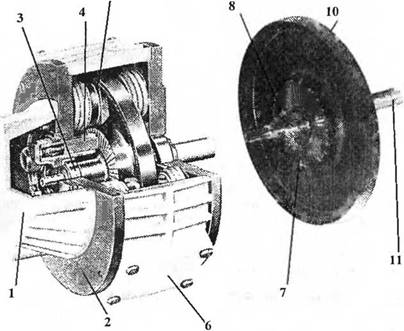
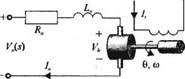
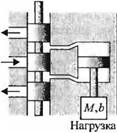
Двигатель постоянного тока — это мощное исполнительное устройство, снабжающее нагрузку энергией, как показано на рис. 2.17(c): схематическое устройство двигателя показано на рис. 2.17(6). На рис. 2.18 изображена в разрезе конструкция такого двигателя. Двигатель преобразует электрическую энергию постоянного тока в механическую энергию вращательного движения. Основная часть момента, создаваемого ротором (якорем) двигателя, используется для управления внешней нагрузкой. Благодаря таким качествам, как высокий вращающий момент, возможность регулирования скорости в широком диапазоне, компактность, хорошие нагрузочные характеристики и одинаковая способность быть использованными в различных системах управления, двигатели постоянного тока широко применяются в роботах-манипулято - рах, лентопротяжных механизмах, дисководах, в машиностроении и исполнительных устройствах следящих систем.
|
Статорная |
|
Щетка Подшипники Инерционная нагрузка |
|
ю’® Инерция = J |
|
Рис. 2.17. Двигатель постоянного тока: (а) эквивалентная электрическая схема и (б) схематическое устройство |
|
|
|
Цель якоря |
|
|
|
Роторная обмотка Щетка |
|
|
|
Цель возбуждения ^ а) |
|
Трение = Ъ Нагрузка |
|
Рис. 2.18. Двигатель постоянного тока плоской конструкции с постоянными магнитами. Двигатели данного типа способны создавать высокий момент при малом моменте инерции ротора. Типичное значение механической постоянной времени — порядка 15 мс. 1 — защитная алюминиевая крышка, 2 — плоская форма, обеспечивающая компактность конструкции, 3 — подшипники со смазкой длительного действия, 4 — щетки с большим сроком службы, 5 — постоянные магниты из сплава алнико, обеспечивающие высокое отношение мощность/вес, 6 — принудительная вентиляция, 7 — обмотка, зафиксированная в эпоксидной среде с высоким диэлектрическим сопротивлением, 8 — медный коллектор, специально обработанный для увеличения срока службы, 9 — якорь с малой индуктивностью, не содержащий деталей из железа, 10 — тарельчатая форма якоря, обеспечивающая малый момент инерции, 11 — вал, изготавливаемый на заказ под специфические нужды потребителя |
Передаточную функцию двигателя постоянного тока мы получим путем линейной аппроксимации реальных характеристик, пренебрегая такими второстепенными эффектами, как гистерезис и падение напряжения на щетках. Входное напряжение может быть подано на обмотку возбуждения либо на якорь. Если отсутствует насыщение, то магнитный поток в воздушном зазоре пропорционален току возбуждения, т. е.
Ф = Kf ij. (2.53)
Предполагается, что момент, развиваемый двигателем, линейно зависит от Ф и тока якоря: Тт = А'Ф /„(г) = KtKf if(t)ia(t). (2.54)
Из уравнения (2.54) вытекает, что для того чтобы двигатель можно было считать линейным элементом, один из токов должен быть постоянным, а второй следует рассматривать в качестве входного тока. Сначала мы рассмотрим двигатель, управляемый по цепи возбуждения, за счет чего обеспечивается значительное усиление по мощности. Преобразуя (2.54) по Лапласу, получим:
TJs) = (KiK/JIj (s) = KJjis), (2.55)
где /0 = /„ есть постоянный ток якоря, а Кт носит название постоянной электродвигателя. Ток возбуждения связан с напряжением возбуждения соотношением
V/(s) = (Rj + Ljs)J/(s). (2.56)
Развиваемый двигателем момент прикладывается к нагрузке. При этом можно записать:
TnXs)=TL(S)+Us). (2.57)
где Tj(s) — момент нагрузки, a TJs) — возмущающий момент, которым часто можно пренебречь. Однако возмущающий момент в ряде случаев принципиально надо учитывать, например, когда на систему действуют внешние силы (скажем, сила от порыва ветра, действующая на антенну). Момент нагрузки в случае ее вращательного движения (см. рис. 2.17) записывается как
|
(2.58) (2.59) (2.60) (2.61) |
T,{s) = Js2Q(s)+ bsB(s).
Из (2.55)-(2.57) имеем:
Ti.(s) = TJs) - Tds), TJs) = Km 1/s).
Vf{s)
Jf(s) =
Rf + LjS
Следовательно, при TJs) = 0 передаточная функция двигателя равна
|
0(5) |
KJJL,
(2.62)
Vf(s) s(Js + b)(LjS + Rf) s(s+ blJ){s + RfILf)
Модель электродвигателя, управляемого по цепи возбуждения, в виде структурной схемы приведена на рис. 2.19. Альтернативное выражение для передаточной функции можно получить, если ввести в рассмотрение постоянные времени:
|
0(5) |
|
(2.63) |
K^/bR,
= C{s) =
Vf(s) s(xjs+ I)(t, s+ 1)
где X/ = Lf/Rj H T, = ЛЬ. Обычно T, > Ту, и постоянной времени обмотки возбуждения можно пренебречь.
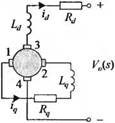
В двигателе, управляемом по цепи якоря, входным (управляющим) воздействием является ток якоря 1Я. Поле, создаваемое статором, может быть образовано током в обмотке возбуждения или постоянными магнитами. В первом случае, если ток возбуждения является постоянным, момент, развиваемый двигателем, определяется как
TJs) = (KxKjIj)la (s) = KJa (4 (2.64)
При использовании постоянных магнитов мы имеем:
TJs) = Кт Ja(s),
где Кт — коэффициент, зависящий от магнитной проницаемости. Ток в цепи якоря связан с напряжением, приложенным к якорю, соотношением
Уа(*) = (Я, + Las)la(s) + Vb{s), (2.65)
где Vb(s) — противоЭДС, пропорциональная скорости вращения. Следовательно,
|
VAs) |
= Кь сф) (2.66)
|
Цепь возбуждения |
Возмущение Tj(s) |
Нагрузка |
Скорость |
|||
|
1 |
Jj(s) |
кт |
ад>-Л^«н |
1 |
И (■'■) |
1 |
|
Rj + LfS |
Js+b |
S |
|
Положение —► 0(5) |
Рис. 2.19. Структурная схема двигателя, управляемого по цепи возбуждения
|
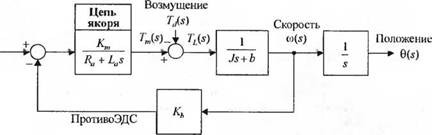
Рис. 2.20. Структурная схема двигателя, управляемого по цепи якоря |
и ток якоря
(2.67)
Я, + О'
Из уравнений (2.58)-(2.59) получим выражение для момента нагрузки:
T/{s) - Js2Q(s) + bs6(s) = Tm(s) - TAs). (2.68)
Связь между переменными, характеризующими динамику двигателя, управляемого по цепи якоря, схематически показана на рис. 2.20. С помощью уравнений (2.64), (2.67) и (2.68) или непосредственно по структурной схеме, полагая TJs) = 0, получим передаточную функцию двигателя:
G(j) = -^- =-------------------- ^------------------ = —---------------- - (2.69)
К, (s) + Las){Js + b)+К hKm] s(s + 2C, o)„s + ш*)
Для многих двигателей, однако, постоянной времени якоря т = La /11а можно пренебречь. Тогда С(-) е<^) Кт KJ(Rab+KbKJ
K,(s) s[RJJs+ b)+К hKm] s(t, s+1)
где эквивалентная постоянная времени т, = RctJI{Rab + A^m).
Интересно заметить, что Кт = Кь. Это можно показать, если рассмотреть установившийся режим работы двигателя и баланс мощностей в предположении, что сопротивлением якоря можно пренебречь. Мощность, подводимая к якорю, равна Кьюіа, а мощность, сообщаемая валу, равна Ты. В установившемся режиме эти мощности равны, так что Kbmia = Ты: поскольку 7’= Kmia (см. 2.64), то отсюда следует, что Кь = Кт.
Электродвигатели применяются для перемещения нагрузки в тех случаях, когда не требуется высокого быстродействия и развиваемой мощности. Типичные параметры такого двигателя приведены в табл.2.4.
|
Таблица 2.4. Типичные параметры электродвигателя постоянного тока мощностью в доли л. с.
|
|
500 400: 300 200 100 70 50 40 30 20 10 7 5 4 3 2 1 0.7 0.5 0.4 0.3 0.2 |
|
V Г Пока lie существующие. А устройства |
|
>, D. а а 2 й ю & ч о о. о X 3 о |
Рис. 2.21
Сравнение по быстродействию и развиваемой мощности электромеханических и электрогидравлических устройств
Прокатные станы. Возможные 4 гидроприводы :
Краны и подъемники;
Типичные. электрогидравлические устройства
Станки
" j "Управление антеннами
Типичные ■ ' Роботы
электромеханические; устройстеа;..;
•Регуляторы ;
автфмббильйых двигателей.
... ;РеіЧуійторьі уровня
5 7 10 20 30 40 50 70 100 200 300 500 1000
400 700
Быстродействие (в обратных единицах)
Более значительной нагрузочной способностью обладают гидравлические исполнительные устройства. На рис. 2.21 показаны в сравнении обычные сферы применения электромеханических и электрогидравлических приводов.
Пример 2.6. Передаточная функция гидравлического исполнительного устройства
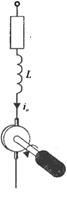
Для линейного перемещения массы может быть использовано гидравлическое исполнительное устройство, приведенное в табл. 2.5 (поз. 9). Подобное устройство способно обеспечить значительное усиление по мощности. Будем считать, что жидкость подается от источника под постоянным давлением и что ее сжимаемостью можно пренебречь. Перемещение золотника вниз, обозначенное через x(t), приводит к поступлению жидкости в верхнюю часть гидроцилиндра и, соответственно, поршень также перемещается вниз. Малая мощность, необходимая для перемещения x(t), преобразуется в высокую мощность, связанную с перемещением поршня y{t). Объемный расход жидкости Q зависит то перемещения x(t) и разности давлений, действующих на поршень, т. е. Q = g(x, Р). Воспользовавшись методом линеаризации путем разложения в ряд Тейлора, запишем:
в = {¥) *+(И] Р=^-крР. (2.71)
где g = g(x, Р) и (хд, Р0) — координаты рабочей точки. Сила, развиваемая поршнем гидроцилиндра, равна произведению его площади А на давление Р, т. е.
А
|
(2.72) |
АР = M^~y+ Ь - dt2 dt
|
(2.73) |
|
dt2 |
|
dt |
|
Подставляя (2.71) в (2.72), получим А |
|
(kyX-Q) |
Кроме того, объемный расход жидкости связан с перемещением поршня соотношением
Q = A^. (2.74)
dt
|
* ^ Ь+ — к, ч |
|
Akx,,d у —-х = М—^ + кр dt2 |
Тогда, подставляя (2.74) в (2.73) и перегруплируя члены, получим:
у - (2-75)
dt
Далее, используя преобразование Лапласа, получим передаточную функцию
|
(2.76) |
У(д) К
X(s) s(Ms+ В)
где
Акх А2
К = —- и В = Ь+ — .
кР К
Заметим, что по форме передаточная функция гидравлического исполнительного устройства совпадает с передаточной функцией электродвигателя. Кроме того, если это исполнительное устройство работает при высоких давлениях и от него требуется большое быстродействие, то в расчетах должен быть принят во внимание эффект сжимаемости жидкости.
Обозначения многих переменных в табл. 2.5 и единицы их измерения помещены на Web-came MCS. Там же можно найти таблицы взаимных преобразований единиц измерения между Международной системой СИ и английской системой единиц.
Понятие передаточной функции и основанные на нем методы являются очень важными, поскольку они предоставляют в распоряжение исследователя и проектировщика столь ценное средство, как математическая модель элементов систем управления. Следует признать, что передаточная функция оказывает неоценимую помощь в попытках получения моделей динамических систем. Особая ценность передаточной функции заключается в том, что ее нули и полюсы на s-плоскости дают полное представление о переходной характеристике системы. В табл. 2.5 приведены передаточные функции некоторых динамических элементов.
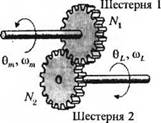
В технике часто требуется передавать вращательное движение от одного вала к другому. Например, в автомобиле мощность, развиваемая двигателем, передается вращающимся колесам через коробку передач и дифференциал. Коробка передач позволяет водителю выбирать то или иное передаточное отношение в зависимости от дорожных условий, тогда как дифференциал находится в неизменном положении. В этом случае скорость движения не является постоянной — водитель может менять ее по своему усмотрению. Другим примером является система редукторов, с помощью которой вращение вала электродвигателя преобразуется в поворот антенны вокруг ее оси. Примерами механических преобразователей данного типа могут служить зубчатые, цепные и ременные передачи. В электрических системах типичным преобразователем является трансформатор. Примером устройства, преобразующего вращательное движение в поступательное, является передача зубчатое колесо-рейка (см. поз. 17 в табл. 2.5).
|
1. Интегрирующая цепь, фильтр |
|
|
|
у2и). 1 ^(s) RCs |
|
2. Дифференцирующая цепь |
|
R
|
|
^ = - RCs |
|
—о+ V&) |
|
3.Дифференцирующая цепь Л, Л2 |
|
V2(s) _ R2(Rfs+ 1) K,(s) Л, |
|
|
|
—0 + |
|
У,(А с |
|
4. Фильтр с интегрированием |
|
K2(s) _ (Rf ]S + 1 )(Rf^s + 1) y,(s) ~ Rf2s |
|
|
|
y,(s) С, _ о-------- |
|
ад |
|
5. Двигатель постоянного тока с управлением по цепи возбуждения (вращательное движение) |
|
|
|
+°—С |
|
6(s) |
|
Vj (s) s(Js + b)(Ljs + Rf) |
6. Двигатель постоянного тока с управлением по цепи якоря (вращательное движение)
|
J, ъ |
|
|
6(s) К,_________
F» s[(Ra + Las)(Js+b)+KhKm]
7. Двухфазный двигатель переменного тока (вращательное движение)
|
0(5) |
|
Vc(s) s{xs + 1) т = J/(b - т) т - наклон линеаризованной зависимости скорости от момента нагрузки (обычно отрицательный) |
|
К.. |
|
•3 |
|
J. b Возбуждение |
8. Электромашинный усилитель
|
|
Vo(s) (K/RcRg) Vc(s) (stc + 1)(їт9 + 1)
Т с Lc/Ro T, J Lq/Rq В режиме холостого хода
id - 0. « Tq
0,05 с < тс < 0,5 с
У12 = Уф Уз4 = К,
9. Гидравлическое исполнительное устройство
|
Возврат Источник давления Возврат |
|
I x{t) Перемещение ^ золотника |
|
Поршень |
|
|
|
Akv |
|
К ■■ |
|
р dg дх |
|
к, = |
|
ё = g(x> Р) = поток А — площадь поршня |
|
т __________ X(s) s{Ms+ В) |
|
. кр=^- р дР |
|
. B = b + |
|
к |
|
р |
|
10. Шестеренчатый редуктор (передача вращения) |
|
|
|
Передаточное число п = Л'гбL =N10111, 0JL = «0)и = тот |
|
11. Потенциометр |
|
|
|
v2(s) _r2_ r2 |
|
F,(s) R Rt + R2 R2 _ 0 Я ~ 0 .... |
|
12. Потенциометрическая схема формирования ошибки П I « |
|
Vzis) = Av(0 - 02(j)) ^2(s) = *A(s) Fn |
|
Vo |
|
0... |
|
о Напряжение ошибки |
|
13. Тахогенератор (датчик скорости) 04- |
|
Вал 0(s),to(j) 1 |
|
V2(s) = = /і/і0(ї) K, = const |
|
ум |
|
14. Усилитель постоянного тока |
|
Vf(s) st+1 R0 — выходное сопротивление C0 — выходная емкость т = RoCo. т« I с и можно пренебречь, если усилитель предшествует сервоприводу |
|
|
^q(s)
|
15. Акселерометр (датчик ускорения) Станина
|
Xm(s) + (b/M)s+ к/М
Для низкочастотных колебаний, где ш < ш№
|
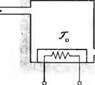
16. Система подогрева |
*,(» ,, ш2 ^О'й) к/м У(з) 1
|
Входной у поток — жидкости |
|
Та Выходной —V поток жидкости |
|
Нагревательный элемент |
|
|
q(s) C, s+ (QS + 1/Л) ГДЄ Т- То-Т,, — разность температур С, — теплоемкость Q — расход жидкости = const 5 — удельная теплоемкость воды R, — тепловое сопротивление изоляции q(s) — тепловая мощность
нагревательного элемента
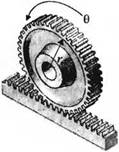
17. Зубчатое колесо и рейка
|
|
х = ИЗ
|
|
преобразует круговое движение в прямолинейное