СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Моделирование систем управления с помощью MATLAB
Многие программные средства анализа и синтеза систем управления (как классическими, так и современными методами) основаны на использовании математических моделей. При описании систем передаточными функциями для этих целей может быть использован MATLAB[1].
В этом разделе мы сначала покажем, насколько полезным может оказаться MATLAB при анализе математической модели механической системы масса-пружина. Используя нотацию MATLAB, мы создадим программу, позволяющую в интерактивном режиме исследовать влияние собственной частоты колебаний и коэффициента затухания на свободное движение массы. При этом мы воспользуемся аналитическим решением, описывающим свободное движение массы.
Далее мы рассмотрим, как MATLAB оперирует с передаточными функциями и структурными схемами. В частности, будет показано, как MATLAB работает с алгебраическими полиномами, вычисляет полюсы и нули передаточных функций, определяет передаточные функции замкнутых систем, производит упрощения структурных схем, вычисляет реакцию систем на единичное ступенчатое воздействие. В заключение мы проиллюстрируем применение MATLAB к синтезу системы управления устройством электрической тяги из примера 2.12.
В этом разделе мы познакомимся с функциями MATLAB roots, tf, series, parallel, feedback, pole, zero, poly, conv, polyval, minreal, pzmap, step.
Система масса—пружина. На рис. 2.2 изображена механическая система масса-пружина с демпфированием. Перемещение массы y{t) описывается дифференциальным уравнением
My(t)+ by(t)+ ky(t) = r(t).
Движение системы при отсутствии внешней силы /■(/) описывается выражением
у(t) = ^=Le<a"' 8ІП(ЮйЛ/і+
лМ2
где 0 = arccos С,, а д>(0) — начальное отклонение. При С, < 1 реакция системы является недо - демпфированной, при С, >1 — передемпфированной, а при С,= 1 — критически демпфированной. С помощью MATLAB мы можем пронаблюдать характер изменения положения массы как реакцию на начальное отклонение ^(0). Рассмотрим случай недодемпфиро - ванной системы:
у{0) = 0,15 м, ши = V2 рад/с, С, = —(к/М = 2, ЫМ = 1).
2V2
|
unforced. m |
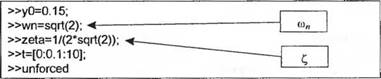
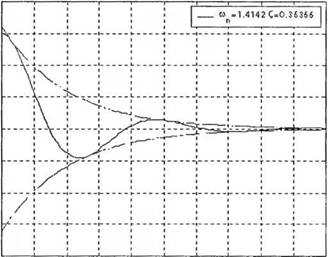
Программа MATLAB для построения графика свободного движения системы приведена на рис. 2.40. Прежде всего, перед запуском программы, в качестве входных данных для основного блока должны быть заданы значения ^(0), ш,„ t и С,. После этого выполняется основная программа unforced. m, которая представляет результат в графической форме. Если возникает необходимость исследовать влияние на свободное движение собственной частоты колебаний и коэффициента затухания, то просто необходимо ввести новые значения ю„ и С, и еще раз выполнить программу. На рис. 2.41 приведен график свободного движения системы. Заметим, что программа автоматически указывает на графике значение коэффициента затухания и собственной частоты колебаний. Это позволяет избежать недоразумений при многократном проведении моделирования.
Рис. 2.40
Скрипт анализа движения системы
«пружина-масса»
%Вычисление реакции на начальное условие %
c=(y0/sqrt(1 - zetaA2)); y=c*exp(-zeta*wn*t).*sin(wn*sqrt(1-zetaA2)*t+acos(zeta));
%
bu=c*exp(-zeta*wn*t); bl=-bu;
|
огибающая |
%
plot(t, y,t, bu,'—',t, bl,'—'), grid хІаЬеІ('Время (с)'), ylabel('y(t) (метры)’) legend(['omega_n=',nurri2str(wn)1' zeta=',num2str(zeta)]);
|
Рис. 2.41 |
0.2 |
|
Свободное |
|
|
движение |
0.15 |
|
системы |
|
|
«пружина-масса» |
|
|
0.1 |
|
|
0.05 |
|
|
С 0 |
|
|
ч |
|
|
•0.05 |
|
|
-0 1 |
|
|
-0.15 |
|
|
-0.2 |
|
01 2345678 9 10 Время (с) |
|
|
В рассмотренной выше задаче мы воспользовались известным аналитическим решением однородного дифференциального уравнения. В общем случае, при моделировании замкнутых систем управления, подверженных влиянию различных внешних воздействий, а также при разных начальных условиях, аналитическое решение бывает получить очень трудно. Здесь можно прибегнуть к помощи MATLAB, который численно решит поставленную задачу и представит результат в графической форме.
MATLAB позволяет исследовать системы, описываемые передаточными функциями. Поскольку передаточная функция имеет вид отношения двух полиномов, мы сначала рассмотрим, как MATLAB оперирует с алгебраическими полиномами. При этом не будем забыват ь, что в передаточной функции должны быть заданы оба полинома— и в числителе, и в знаменателе.
|
|
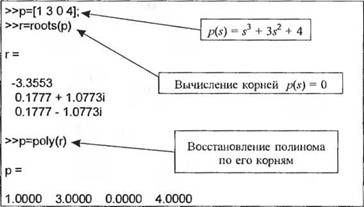
Полиномы в MATLAB представляются в виде векторов-строк, состоящих из коэффициентов в убывающем порядке степеней. Например, полином p(s) = s' + 3s2 + 4 задается так, как показано на рис. 2.42. Обратите внимание, что даже если коэффициент при ка - кой-то степени равен нулю, он все равно включается в представление полинома p(s).
Рис. 2.42
Ввод полинома /0(s) = s3 + 3s2 + 4 и вычисление его корней
Если р есть вектор-строка, состоящая из коэффициентов p(s) в порядке убывания степеней, то функция roots(p) определяет вектор-столбец, содержащий корни этого полинома. И наоборот, если г — вектор-столбец, содержащий корни полинома, то функция poly(r) дает вектор-строку из коэффициентов полинома в убывающем порядке степеней. На рис. 2.42 показано, как с помощью функции roots вычисляются корни полинома p(s) = = s3 + Зі2 + 4. На рис. 2.42 показано также, как можно восстановить полином по его корням с помощью функции poly.
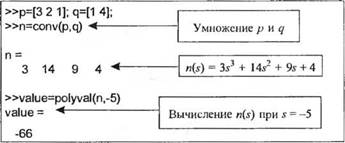
Умножение полиномов производится с помощью функции conv. Предположим, что мы хотим получить полином n(s) в развернутой форме, где n(s) = (Зі2 + 2s + 1 )(.s + 4). Эта процедура выполняется так, как показано на рис. 2.43. В результате умножения получаем полином n(s) = 3s3 + 14s2 + 9s + 4. Для вычисления значения полинома при заданном значении переменной используется функция polyval. Как показано на рис. 2.43, полином n(s) имеет значение п(-5) = -66.
В пособиях по применению MATLAB модели линейных стационарных систем рассматриваются в качестве объектов, позволяя манипулировать ими как единым целым. При использовании аппарата передаточных функций модели систем создаются с помощью функции tf; если модель должна быть представлена в переменных состояния, то применяется функция ss (см. главу 3). Применение функции tf проиллюстрировано на рис. 2.44(a). Благодаря возможностям объектно-ориентированного программирования, присущим MATLAB, модели систем обладают свойствами объектов, которые легко можно изменять; аналогично, функции, применяемые для работы с объектами, принято называть методами. Например, если вы имеете две модели систем,
|
1 5+1* |
10
|
G (*) = - |
и G2(s) =
5' +2s+5
то вы можете сложить их с помощью оператора «+»:
G(s) = С, (s)+G2 (s) = f tgl+15 .
s +3i' + 7s+5
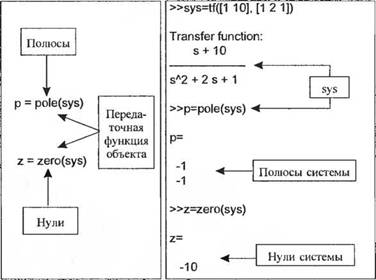
Соответствующая программа MATLAB приведена на рис. 2.44(6), где sysl представляет передаточную функцию G[(.v), a sys2 — G2(s). Вычисление полюсов и нулей передаточной функции производится при работе с ней как с объектом путем применения функций pole и zero. Это проиллюстрировано на рис. 2.45.
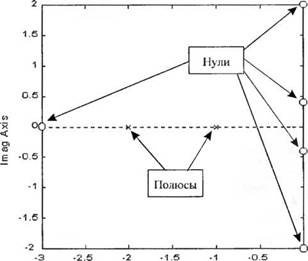
В следующем примере мы покажем, как с помощью функции pzmap (рис. 2.46) можно указать расположение на комплексной плоскости полюсов и нулей передаточной функции. Нули на диаграмме обозначаются кружочками, а полюсы — крестиками. Если функция pzmap вызывается без аргументов, то диаграмма строится автоматически.
|
|
|
Рис. 2.43 Использование функций conv и polyval для умножения полиномов (3s2 + 2s + 1 )(s + 4) и вычисления значения произведения |
|
G](j) |
|
Передаточная функция объекта |
|
G(s) = |
|
den |
|
Рис. 2.44 (а) Функция tf; (б) Применение функции tf для образования передаточных функций объектов и их сложение с помощью оператора «+» |
|
sA2 + 2 s + 5 »num2=[1]: den2=[1 1]; »sys2=tf(num2,den2) Transfer function: 1 |
|
»num1=[10]; den1=[1 2 5]; »sys1=tf(num1,den1) Transfer function: 10 |
|
G2(s) |
|
sys = tf(num, den) |
s + 1
»sys=sys1 +sys2
Transfer function: sA2 + 12 s + 15
G,(s) • g2(s)
sA3+ 3 sA2 + 7 s + 5
|
б) |
а)
|
|
|
Рис. 2.45 (а) Функции pole и zero; (б) Применение функций pole и zero для вычисления полюсов и нуля линейной системы |
|
а) б) |
Пример 2.16. Передаточные функции
Рассмотрим передаточные функции
г, л +1 и/л (s+l)(s+2)
СС0 = 1—- г -—: и H(s) =
.Vі + Зі2 + 3s + 1 (s+ 2i)(s-2i)(j+ 3)
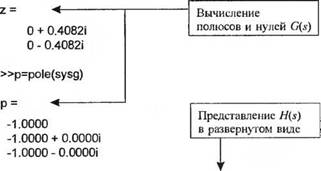
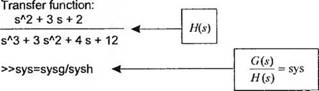
С помощью программы MATLAB мы можем вычислить полюсы и нули G(s), получить характеристические уравнение для H(s), разделить G(s) на H(s), а также получить на комплексной плоскости картину расположения полюсов и нулей функции G(s)!H(s).
|
Pole-zero map
Real Axis |
|
Рис. 2.46 Функция pzmap |
|
ik |
т > num G(s)-—— = sys den |
|
[P, Z]=pzmap(sys) |
|
Р: полюсы в виде вектора-столбца Z: нули в виде вектора-столбца |
Рис. 2.47
Расположение полюсов и нулей функции G{s)/H(s)
Расположение полюсов и нулей передаточной функции G(s)/H(s) показано на рис. 2.47, соответствующие инструкции MATLAB приведены на рис. 2.48. На картине ясно видно расположение пяти нулей и всего двух полюсов. В действительности этого не может быть. т. к. известно, что число полюсов дожпо быть больше или равно числу нулей. Используя функцию roots, мы можем убедиться, что на самом деле четыре полюса находятся в одной и той же точке s = - l. Таким образом, функция pzmap не позволяет различить кратные полюсы или нули.
Модели в виде структурных схем. Предположим, что мы получили математические модели объекта управления, регулятора и, возможно, многих других элементов системы, таких как датчики и исполнительные устройства, причем эти модели представлены в виде передаточных функций. Дальнейшая цель состоит в том, чтобы объединить все эти элементы в единую структуру, создав тем самым систему управления. С помощью MATLAB можно выполнить все необходимые преобразования структурной схемы.
Простейшую разомкнутую систему управления можно получить, соединив последовательно объект управления и регулятор, как это показано на рис. 2.49. Как с помощью MATLAB определить передаточную функцию, связывающую R(s) и У(л), будет продемонстрировано в следующем примере.
»numg=[6 0 1]; deng=[1 З 3 1]; sysg=tf(numg, deng); »z=zero(sysg)
|
|
|
Рис. 2.48 Операции с передаточными функциями G(s) и H(s) |
»n1=[1 1]; n2=[1 2]; d1=[1 2*i]; d2=[1 -2*i];d3=[1 3]; »numh=conv(n1 ,n2); denh=conv(d1 ,conv(d2,d3)); »sysh=tf(numh, denh)
|
|
Transfer function: 6 sA5 + 18 sA4 + 25 sA3 + 75 sA2 + 4 s + 12
|
Картина расположения полюсов и нулей_________ |
sA5 + 6 sM + 14 sA3 + 16 sA2 + 9 s + 2 » pzmap(sys) <
Рис. 2.49
Разомкнутая система управления
|
Регулятор |
t/(s) |
Объект |
|
|
Gc{s) |
G(s) |
|
од- |
Пример 2.17. Последовательное соединение
Пусть объект управления задан передаточной функцией G(s) = 1/500 s2, а регулятор имеет передаточную функцию Gc(s) = (s + l)/(s + 2). На рис. 2.50 изображено последовательное соединение двух систем с передаточными функциями С|(л) и G2(s), а также проиллюстрирован смысл функции series, а нарис. 2.51 показано, как с ее помощью определяется произведение Gc(s)G(s). Результирующая передаточная функция имеет вид
Gc(s)G(s) =--------------- г = sys,
500s + 1000s2
где sys есть обозначение передаточной функции в программе MATLAB.
В структурных схемах очень часто встречается параллельное соединение элементов. В таких случаях для определения передаточной функции соединения используется функция parallel. Смысл этой функции поясняет рис. 2.52.
|
Система 1 |
Система 2 |
||
|
G,(s) |
Сф) |
|
Y(s) |
|
Рис. 2.50 (а) Структурная схема; (б) Функция series |
|
о) |
|
т- |
|
б) |
|
т, ^ y('v) Т (s) =---- = sys t7(s) %-------------------- |
|
Gi(s) = sysl |
|
Сг(.ї) = sys2 |
[sys]=series(sys1 ,sys2)
|
a) |
|
ад—► |
|
ОД = |
|
500/ |
|
Рис. 2.51 Применение функции series |
|
6) |
»numg=[1]; deng=[500 0 0]; sysg=tf(numg, deng); »numh=[1 1]; denh=[1 2]; sysh=tf(numh, denh); »sys=series(sysg, sysh);
|
Transfer function: s + 1 |
»sys
|
Рис. 2.52 (а) Структурная схема; (б) Функция parallel |
500 sA3 + 1000 sA2
|
Система 1 |
|||
|
G,(s) |
+ |
||
|
с |
|||
|
Система 2 |
+t |
||
|
G_,(s) |
|
m- |
б)
|
G|(s) = sysl |
|
G2(s) = sys2 |
T(s) = = sys
U(s)
A------
[sys]=parrallel(sys1 ,sys2)
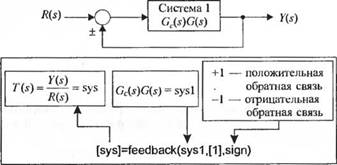
Мы можем ввести в рассмотрение сигнал обратной связи, замкнув контур единичной обратной связью, как показано на рис. 2.53. В этом случае £a{s) есть изображение по Лапласу сигнала ошибки, a R(s) — эталонного входа. Передаточная функция замкнутой системы определяется выражением
Сс (5X7(5)
т-
(1+GC (s)G(s))
С помощью функции feedback мы имеем возможность упростить структурную схему, вычислив передаточную функцию замкнутой системы. Эта функция применима как к одноконтурным, так и к многоконтурным системам управления.
Рис. 2.53 + е„ (s)
Система управления R(s) '
с единичной обратной ±J 1
связью
|
Регулятор |
U(s)t |
Объект |
||
|
Сф) |
G(s) |
|
Часто встречается случай, когда замкнутая система имеет единичную обратную На рис. 2.55 изображена система с неединичной обратной связью и проиллюстриро- Рис. 2.54 , (а) Структурная (б) Применение |
|
Рис. 2.55 (а) Структурная схема; (б) Функция feedback |
|
о) |
|
T (s) = = sys /?(*) |
G(s) = sysl |
H(s) = sys2 |
+1 — пол. обр. связь —1 - отр. обр. связь |
|
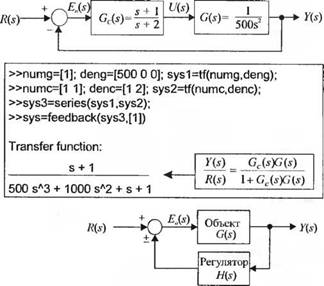
Пример 2.18. Применение функуции feedback к системе с единичной обратной связью Пусть передаточные функции объекта и регулятора на рис. 2.51(a) соответственно равны G(s) и Gc(s). Чтобы воспользоваться функцией feedback, сначала нам необходимо применить функцию series, чтобы вычислить произведение G(s)Gc(s). Эта последовательность действий приведена на рис. 2.56(6). В соответствии с рис. 2.56(6), передаточная функция замкнутой системы равна = = ,*+1 = l + Gc(s)G(s) 500s + 1000s + s + 1 |
|
у у у [sys]=feedback(sys1 ,sys2,sign) |
|
|
|
Система 1 |
|
■* № |
|
R(S)------- ►О |
|
G(s) |
|
Система 2 H(s) |
|
б) |
|
|
|
Рис. 2.57 Система с регулятором в цепи обратной связи |
|
Рис. 2.56 (а) Структурная схема; (б) Применение функции feedback |
|
а) |
|
б) |
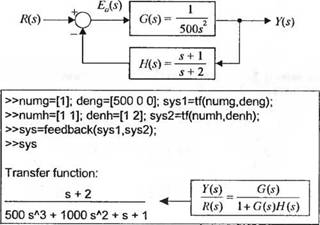
Другая конфигурация системы с обратной связью приведена на рис. 2.57. В данном случае регулятор находится в цепи обратной связи. Замкнутая система имеет передаточную функцию
G(s)
T(s) =
1+G(s)N(s)
Пример 2.19. Функция feedback
Пусть объект и регулятор имеют, соответственно, передаточные функции G(s) и H(s), как показано на рис.2.58(а). Для определения передаточной функции замкнутой системы воспользуемся функцией feedback. Соответствующая программа приведена на рис. 2.58(6). В результате получим
|
ТҐ s+2 7 (s) = г---------------------------------- = sys. 500s3 + 1000s2 + s+l
|
|
а) б) |
Рис. 2.58
Применение функции feedback:
(а) Структурная схема;
(іб) Скрипт MATLAB
Функции MATLAB series, parallel и feedback могут оказаться полезными при упрощении структурных схем многоконтурных систем.
Пример 2.20. Упрощение многоконтурной системы
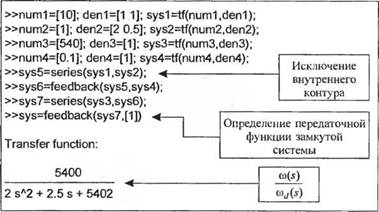
Многоконтурная система изображена на рис. 2.26. Наша цель — определить передаточную функцию T(s) = Y(s)/R(s), если
С-(у) = —тт;- С2М = - Ц. G3(s)= 2 ~l, G4(s) = -~ //,(,)= 2. H3(s)= L
s+10 s+1 s + 4s+4 s + 6
В данном примере все действия сводятся к пяти этапам:
□ Этап 1. Ввести все передаточные функции в программу MATLAB.
□ Этап 2. Перенести узел через блок С4 в направлении движения сигнала.
□ Этап 3. Исключить контур G^GJit.
□ Этап 4. Исключить конту р, содержащий Н2.
□ Этап 5. Заменить оставшийся контур одним блоком и записать выражение T(s). Соостветствующие операции показаны на рис. 2.27, а программа, выполняющая их, приведена на рис. 2.59. Выполнение программы дает следующий результат:
s5 + 4/ + 6s3 + 6s2 + 5s + 2 SyS ~ 12s6 + 205s5 + 1066s4 + 2517s3 + 3128s2 + 2196s+ 712 '
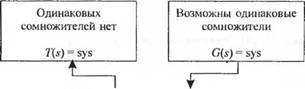
При определении передаточной функции замкнутой системы следует соблюдать осторожность. Передаточная функция определяет соотношение между входом и выходом после сокращения одинаковых нулей и полюсов. Если мы вычислим полюсы и нули T(s), то обнаружим, что полиномы в числителе и знаменателе имеют одинаковый сомножитель (s + 1) . Эти сомножители необходимо сократить, прежде чем утверждать, что мы действительно получили передаточную функцию. В сокращении нуля и полюса нам может помочь функция minreal. Ее смысл поясняет рис. 2.60. Заключительная процедура в упрощении ст руктурной схемы состоит в удалении одинаковых сомножителей из числителя и знаменателя 7’(s), как показано на рис. 2.61. Итоговый результат также приведен на этом рисунке. После применения функции minreal можно видеть, что порядки полиномов в числителе и знаменателе уменьшились на единицу за счет сокращения одного полюса и одного нуля.
|
Рис. 2.59 Упрощение многоконтурной системы |
|
Этап 1 Этап 2 Этап З Этап 4 Этап 5 |
|
»ng1=[1]; dg1=[1 10]; sysg1=tf(ng1,dg1); »ng2=[1]; dg2=[1 1]; sysg2=tf(ng2,dg2); »ng3=[1 0 1 ]; dg3=[1 4 4]; sysg3=tf(ng3,dg3); »ng4=[1 1]; dg4=[1 6 ]; sysg4=tf(ng4,dg4) »nh1=[1 1]; dh1=[1 2]; sysh1=tf(nh1,dh1); »nh2=[2]; dh2=[1]; sysh2=tf(nh2,dh2); »nh3=[1]; dh3=[1]; sysh3=tf(nh3,dh3); »sys1=sysh2/sysg4; »sys2=series(sysg3,sysg4); »sys3=feedback(sys2,sysh1,+1); »sys4=series(sysg2,sys3); »sys5=feedback(sys4,sys1); »sys6=series(sysg1 ,sys5); »sys=feedback(sys6,[1]) |
Transfer function: sA5 + 4 sA4 + 6 sA3 + 6 sA2 + 5 s + 2 12 sA6 + 205 sA5 + 1066 sA4 + 2517 sA3 + 3128 sA2 + 2196 s + 712
Рис. 2.60 Функция minreal
|
sys=minreal(sys1) |
|
Рис. 2.61 Применение функции minreal |
|
Сокращение одинаковых сомножителей |
»num=[1 4 6 6 5 2]; den=[12 205 1066 2517 3128 2196 712]; »sys1=tf(num, den); »sys=minreal(sys1); <■ Transfer function: 0.08333 sA4 + 0.25 sA3 + 0.25 sA2 + 0.25 s + 0.1667 sA5 + 16.08 sA4 + 72.75 sA3 + 137 sA2 + 123.7 s + 59.33
Пример 2.21. Управление устройством электрической тяги
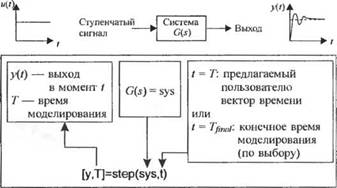
В заключение мы еще раз вернемся к системе управления устройством электрической тяги из примера 2.12. Структурная схема этой системы приведена на рис. 2.35(e). Здесь мы вычислим передаточную функцию замкнутой системы и исследуем реакцию скорости ca(s) на задающее воздействие (ojs). Первый этап, проиллюстрированный программой на рис. 2.62, состоит в определении передаточной функции T(s) = ш(ї)/ш()(ї). Характеристическое уравнение замкнутой системы имеет второй порядок, причем сои = 52 и (, = 0,012. Поскольку коэффициент затухания очень мал, следует ожидать, что реакция системы будет иметь сильно колебательный характер. Реакцию ы(/) на эталонный вход соJt) можно исследовать с помощью функции step. Эта функция, смысл которой поясняет рис. 2.63, вычисляет реакцию линейной системы на единичное ступенчатое воздействие. Ступенчатая функция имеет важное значение потому, что качество систем управления обычно оценивается по их реакции на воздействие данного вида.
Если единственной целью исследований является получение графика y{t), то функцию step можно использовать без указания аргументов в левой части инструкции. График будет получен автоматически с указанием переменных по осям координат. Если же y(t) необходимо для каких-то других целей кроме построения графика, то функцию step надо использовать с указа-
|
|
|
Рис. 2.62 Упрощение структурной схемы системы электрической тяги |
|
|
|
а) б) |
Рис. 2.63 Функция step
нием всех аргументов в левой части инструкции, после чего вывод графика осуществляется с помощью функции plot. Переменная / определяется как вектор-строка, состоящая из моментов времени, в которые мы желаем получить значения выходной переменной y(t).
В программе MATLAB можно также задать значение t = tf, так что переходная характеристика будет вычислена на интервале от t = 0 до / = tj, и кроме того указать число точек в этом интервале.
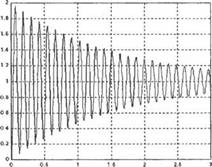
Переходная характеристика электропривода приведена на рис. 2.64. Как и ожидалось, выходная переменная у(1) = ы(/). т. е. скорость вращения, имеет сильно колебательный характер.
|
|
|
Время (с) |
|
Рис. 2.64. (a) Переходная характеристика электропривода; (б) Скрипт MATLAB |
|
б) mresp. m |
|
%Эта программа вычисляет %переходную характеристику %электропривода % num=[5400]; den=[2 2.5 5402]; sys=tf(num, den); t=[0:0.005:3]; [y, t]=step(sys, t); plot(t, y),grid хІаЬеІ('Время (c)‘) у1аЬе1(‘Скорость вращения’) |
|
а) |