СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Качество системы второго порядка
Рассмотрим одноконтурную систему второ-
|
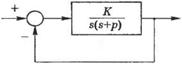
го порядка и найдем ее реакцию на единичное ступенчатое воздействие. Для системы, изображенной на рис. 5.4. можно записать: |
|
К s(s+p) |
|
Рис. 5.4. Замкнутая система управления |
|
1 + G(j) s - + pS + К Используя обозначения, введенные в разд. 2.4, перепишем (5.6) в виде |
|
(5.5) |
|
£(«) |
|
|
|
G(s)= |
|
■R(s) |
|
Y(s) |
|
(5.6) |
С0„
|
т R(s). |
|
(5.7) |
Г(*) = -
s' +2^юия+со"
При единичном ступенчатом входном воздействии получим:
to;
|
(5.8) |
14s) = -
s(s2 + 2C,®„s + to2 )
Воспользовавшись таблицей преобразований Лапласа (табл. 5.3), найдем оригинал:
ЯО = 1-^-^"'5Іп(ш„р; + Є), (5.9)
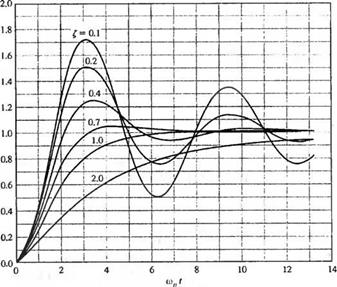
где р = д/і-^2,0 = arccos С, и 0 < ^ < 1. На рис 5.5 (а) изображены переходные характеристики этой системы для различных значений коэффициента затухания С,. С уменьшением С,
корни характеристического уравнения замкнутой системы приближаются к мнимой оси и реакция становится сильно колебательной. На рис. 5.5 (б) приведены те же переходные характеристики в зависимости от параметра С, и времени.
В случае единичной импульсной функции, для которой изображение по Лапласу R(s) = 1, можно записать:
|
(5.10) |
со:
Y(s) =
7 9 9
s~ +2C, a„s+®~
|
|
|
12.0 |
|
14.0 |
Рис. 5.5
(а) Переходные характеристики системы второго порядка при ступенчатом входном сигнале.
|
а) |
(б) Те же характеристики в зависимости от £ и времени
|
10 |
|
Рис. 5.6 |
1.0 |
|
Реакция системы |
|
|
второго порядка |
0.8 |
|
на импульсную |
|
|
входную функцию |
0.6 |
|
0.4 |
|
|
0.2 |
|
|
АО |
|
|
О О 1 7 3 |
|
|
-0.2 |
|
|
-0.4 |
|
|
-0.6 |
|
|
-0.8 |
4 5
со,,/
что совпадает с передаточной функцией замкнутой системы T(s) = Y(s)/R(s). Реакция системы на единичную импульсную функцию определяется выражением
со.,
|
(5.11) |
y(t) = - r-e sinco„pr,
которое является производной от реакции на единичную ступеньку. На рис. 5.6 изображены реакции системы второго порядка на единичную импульсную функцию для различных значений параметра При определении показателей качества проектировщик может использовать реакцию системы как на ступенчатую, так и на импульсную функцию.
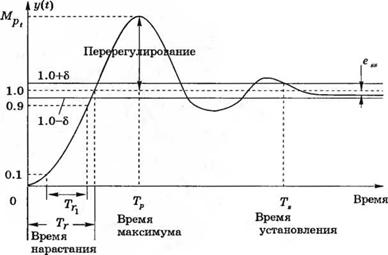
Типовые показатели качества обычно определяются по виду реакции на ступенчатое входное воздействие, как показано на рис 5.7. Быстродействие системы напрямую связа-
|
|
|
Рис. 5.7 Реакция системы управления на ступенчатое воздействие |
но с временем нарастания Тг и временем максимума переходной характеристики Тр. Для недодемпфированных систем, переходная характеристика которых обладает перерегулированием, время нарастания определяется как время изменения реакции от 0 до 100% заданного значения выходной переменной. Если система передемпфирована, то перерегулирование отсутствует, время максимума смысла не имеет, а в качестве времени нарастания Т рассматривается интервал, в течение которого переходная характеристика изменяется от 10% до 90% ее значения. Насколько хорошо действительная реакция системы соответствует ступенчатому входному сигналу, оценивается по относительному перерегулированию и времени установления Ts. При единичном ступенчатом воздействии относительное перерегулирование (ОП) определяется как
М„ — к. з.
О. П. = —р - 100%, (5.12)
к. з.
где Мр — максимальное значение переходной характеристики, а к. з. — ее конечное значение. Обычно к. з. совпадает с величиной входной ступеньки, но во многих системах оно существенно отличается от желаемого значения, определяемого входным сигналом. Для системы, описываемой уравнением (5.8), к. з. = 1.
Время установления Ts определяется моментом, после которого переходная характеристика остается полностью внутри зоны, отличающейся от величины входного воздействия на +8%. Данная зона изображена на рис 5.7. Для системы второго порядка, реакция которой описывается выражением (5.9), время установления Тх можно найти по моменту, начиная с которого реакция отличается от своего конечного значения не более, чем на 2%, т. е. если
e-Ws <0,02,
Т, * 4.
|
:4т = |
Следовательно,
(5.13)
Таким образом, время установления можно считать равным четырем постоянным времени т, где х = 1Я>„ — постоянная времени, соответствующая доминирующим корням характеристического уравнения. По реакции системы на ступенчатое воздействие можно также определить установившуюся ошибку, как это показано на рис. 5.7.
Реакцию системы на ступенчатое воздействие можно охарактеризовать двумя факторами:
1. Быстродействием, которое определяется временем нарастания и временем максимума.
2. Близостью к желаемому виду, которая определяется перерегулированием и временем установления.
По своей сути эти факторы являются противоречащими друг другу, что заставляет искать определенный компромисс.
Чтобы получить зависимость показателей Мп и Тр от параметра С,, можно продифференцировать выражение (5.9) и приравнять производную нулю. Другой способ основан на
использовании свойства дифференцируемости преобразования Лапласа, которое записывается в виде
>(0~
= sY(s
dt
|
(5.14) |
при условии, что начальное значение y(t) равно нулю. В результате мы можем получить производную от_у(0, умножив выражение (5.8) над, что даст нам правую часть выражения (5.10). Применив обратное преобразование Лапласа к последнему выражению, мы получим (5.11), которое обращается в нуль при ю„ р< =п. Отсюда выражение для времени максимума переходной характеристики системы второго порядка:
|
т - .... |
71 |
|
1-С2 |
а максимальное значение переходной характеристики,
|
(5.15) |
Мр= 1+e-W^.
|
(5.16) |
В результате относительное перерегулирование составляет
ОП = 100е
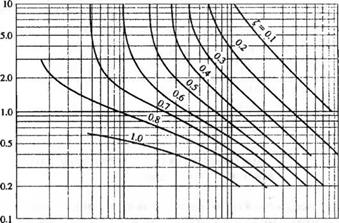
Зависимость относительного перерегулирования от коэффициента затухания С, представлена на рис. 5.8. Здесь же изображена зависимость нормированного времени максимума (йпТр от коэффициента затухания С,. Для некоторых значений коэффициента затухания С, величина относительного перерегулирования представлена в таблице 5.2. И снова мы сталкиваемся с необходимостью поиска компромисса между скоростью реакции и допустимым перерегулированием.
Таблица 5.2. Относительное перерегулирование (в %) в зависимости от коэффициента затухания для системы второго порядка
Коэффициент затухания Относительное перерегулирование
0,9 0,8 0,7 0,6 0,5 0.4 0.3
0,2 1,5 4,6 9,5 16,3 25,4 37,2
|
5.00 4.80 4.60 4.40 4.20 4.0 Ю"ТР 3.80 3.60 3.40 3.20 3.00 |
|
о к л ч О) Еч К ^ о * о и Ен О Я К о й ej |
Рис. 5.8
Зависимость относительного перерегулирования и нормированного времени максимума от коэффициента затухания для системы второго порядка
|
V 1 1 1 1 I 1 Относительное |
|||||||||
|
* |
іерє |
per |
улк |
ров |
ан* |
ІЄ |
|||
|
/ |
°пТр |
||||||||
|
г |
|||||||||
|
У |
/ |
||||||||
|
ч |
V |
/ |
|||||||
|
< |
|||||||||
|
100 90 80 70 60 50 40 30 20 10 |
|
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Коэффициент затухания, £ |
Рис. 5.9
|
|
Зависимость нормированного времени нарастания ТГу от С для системы второго порядка
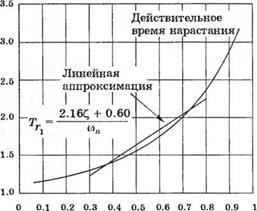
Скорость реакции системы на ступенчатое воздействие можно оценить временем ее нарастания от 10% до 90% величины ступеньки. В таком определении время нарастания Т указано на рис. 5.7. Нормированное время нарастания «>„7^ в зависимости от С,
(0,05 < С, < 0,95) изображено графически на рис 5.9. Действительную кривую Тг трудно описать аналитически, однако можно воспользоваться линейной аппроксимацией
|
(5.17) |
2,16^+0,60
Т,=
которая является достаточно точной для 0,3 < £ < 0,8. Данная аппроксимация приведена на рис. 5.9.
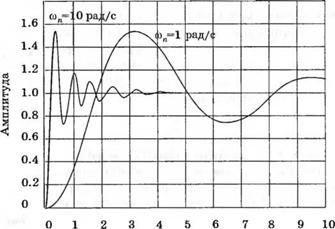
Скорость реакции на ступенчатый входной сигнал, описываемая выражением (5.17), зависит от С, и со,,. При данном С, реакция тем быстрее, чем больше со,,, как показано на рис 5.10. Заметим, что перерегулирование не зависит от co„.
|
Время (с) |
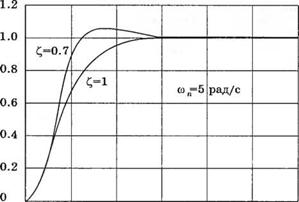
При данном ю„ реакция тем быстрее, чем меньше С,, как показано на рис. 5.11, однако ее скорость ограничивается допустимым перерегулированием.
Рис. 5.10
Реакция системы второго порядка на ступеньку при £ = 0,2, со„ = 1
и о>„ = 10
|
|
|
Рис. 5.11 Реакция системы второго порядка на ступеньку при шл = 5, £ = 0,7 и £ = 1 |
|
W >> н К 4 с 5 С |
|
2.5 |
|
3.0 |
|
0.5 1.0 1.5 2.0 Время (с) |
5.4. Влияние третьего полюса и нуля
на характеристики системы второго порядка
Кривые, изображенные на рис. 5.8, являются точными только для системы второго порядка, определяемой выражением (5.8). Тем не менее они являются весьма полезными и для многих других систем, обладающих парой доминирующих корней, реакция которых на ступенчатое воздействие может быть представлена в виде рис. 5.8. Такой подход, хотя и является приближенным, позволяет обойтись без применения обратного преобразования Лапласа для оценки относительного перерегулирования и других показателей качества. Например, для системы третьего порядка, имеющей в замкнутом состоянии передаточную функцию
T(s) = —------- 1-------------- , (5.18)
(s2 +2ф+ l)(ys+1)
|
JCо |
|
А = КОрнИ замкнутой |
расположение ее корней показано на рис. 5.12 (здесь предполагается, что w„ = 1). Экспериментально было установлено, что относительное перерегулирование, ОП, и время установления, Ts, для данной системы соответствуют кривым для системы второго порядка, если
|1/У|> Ю|Сши|.
Иными словами, реакцию системы третьего порядка можно аппроксимировать с помощью доминирующих корней системы второго прядка, если только действительная часть этих корней меньше 1/10 действительной части третьего
корня. Рис. 5-12. Положение корней
системы третьего порядка на 5-плоскости
С помощью вычислений на компьютере для С, = 0,45 можно найти реакцию системы на единичное ступенчатое воздействие. При у = 2,25 реакция является монотонной (система передемпфирована), т. к. действительная часть комплексных полюсов равна - 0,45, тогда как вещественный полюс равен — 0,444. Время установления (по критерию 2% от конечного значения) составляет 9,6 с. При у = 0,90, или 1/у = 1,11, в сравнении с = 0,45 мы видим, что перерегулирование составляет 12%, а время установления равно 8,8 с. Если бы комплексные корни были доминирующими, то перерегулирование составляло бы 20%, а время установления равнялось бы 4/<^ш(1 = 8,9 с. Результаты расчетов сведены в табл. 5.3.
|
Таблица 5.3. Влияние третьего полюса при С, = 0,45
|
* Примечание-. Время установления нормировано, т. е. приведено в значениях со„7Л и определено по критерию 2%.
Следует также заметить, что показатели качества, отмеченные на рис. 5.8, имеют силу только тогда, когда передаточная функция не имеет конечных нулей. Если же передаточная функция содержит конечные нули, которые располагаются достаточно близко к доминирующим комплексным полюсам, то эти нули будут оказывать существенное влияние на вид переходной характеристики системы.
На переходную характеристику системы с одним нулем и двумя полюсами сильное влияние оказывает положение нуля. На рис. 5.13(a) приведена номограмма для определения относительного перерегулирования при ступенчатом входном воздействии для системы с передаточной функцией
T(s)= ,
s' +2C, a>ris+(i)-
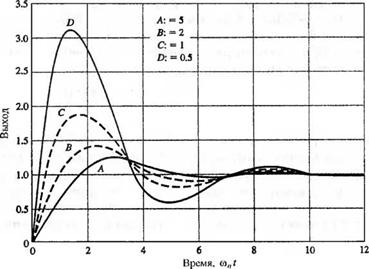
причем кривые построены для С, < 1 в зависимости от о/^(оп. Сами же переходные характеристики для нескольких значений а/С, ш„ приведены на рис. 5.13(6). Важнейшие показатели качества для этих значений a/C, on при С, = 0,45 представлены в табл.5.4.
Связь между положением на s-плоскости полюсов передаточной функции замкнутой системы и ее переходной характеристикой играет важную роль при выборе требований, предъявляемых к системе. Чтобы проиллюстрировать это, мы рассмотрим простой пример.
|
Таблица 5.4. Показатели качества системы второго порядка с параметром £=0,45 при наличии нуля
|

Примечание: Время нормировано, т. е. приведено в значениях соа время установления определено по критерию 2%.
|
|
|
а |
|
500 1000 |
Рис. 5.13
|
а) |
(а) Зависимость относительного перерегулирования от £ и со„ для системы второго порядка, передаточная функция которой содержит нуль.
(б) Переходные характеристики системы второго порядка
|
|
|
10 20 50 100 200 Относительное перерегулирование |
с параметром £ = 0,45, передаточная функция которой содержит нуль, для четырех значений отношения а/Стл:
А =5, В = 2,
|
б) |
С = 1 и D = 0,5
Пример 5.1. Выбор параметра
|
|
На рис. 5.14 изображена одноконтурная система управления. Необходимо выбрать коэффициент усиления К и параметр р так, чтобы удовлетворить требования, предъявляемые к переходной характеристике системы. Пусть система должна обладать как рис. 5.14. Одноконтурная система можно большим быстродействием и при управления
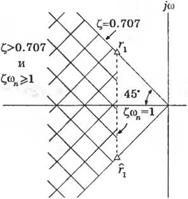
этом перерегулирование не должно превышать 5%. Время установления переходной характеристики внутри зоны 2% от ее конечного значения должно быть не более 4 с. Коэффициенту затухания £ = 0,707 соответствует перерегулирование 4,3%. Линия постоянного коэффициента затухания для С, = 0,707 изображена на рис. 5.15. Поскольку время установления 4
|
Рис. 5.15. Область расположения корней на s-плоскости, отвечающая требованиям к качеству системы |
Ts. = —- < 4 с.
то мы должны потребовать, чтобы действительная часть комплексных полюсов передаточной функции T(s) удовлетворяла условию Cf. а„ > 1. Область «-плоскости, удовлетворяющая обоим требованиям к переходной характеристике, отмечена на рис. 5.15 штриховкой.
Если выбрать корни замкнутой системы г, = -1 +J и Р, = -1 - j, то мы будем иметь Ts = 4 с и перерегулирование 4,3%. Следовательно, С, = 1/V2 и и„ = 1/С = л/2. Передаточная функция замкнутой системы C(s) К со*
1 + G(s) s +ps + K s + 2^0,/. + oil
Таким образом, нам необходимо иметь К = со2 = 2 и
|
разделах. |
р = 2Cfiin = 2 . Исследователь и проектировщик систем управления должен отчетливо представлять связь между положением корней замкнутой системы и ее переходной характеристикой. Поэтому данному вопросу мы уделим большее внимание в последующих
Пример 5.2. Доминирующие полюсы 71s)
Рассмотрим систему, передаточная функция которой в замкнутом состоянии имеет вид:
M"U+a)
R(s) (s2 + 2£co„s + ь>2)(1 + ts)
На переходную характеристику могут оказывать влияние как нуль, так и вещественный полюс. Если я з> Qon и т « £ыи, то это влияние будет незначительным.
Предположим, что мы имеем
T(s)- 62,5(5 + 2,5)
(s2 + 6j + 25)(s + 6,25)
Заметим, что ДО) = 1, т. е. коэффициент усиления системы на нулевой частоте равен единице, поэтому следует ожидать, что при ступенчатом входном сигнале установившаяся ошибка будет равна нулю. В нашем случае Cf£>„ = 3, т = 0,16 и а = 2,5. Положение полюсов и нуля на
s-плоскости показано на рис. 5.16. В качестве первого приближения пренебрежем вещественным полюсом и получим:
|
;со |
|
>4 }2 |
|
х |
TWmWE±VI.
|
-3 |
s + 6s + 25
|
-х- |
|
-2.5 |
|
- 6.25 |
|
-J2 -)4 |
|
X |
|
Рис. 5.16. Положение на s-плоскости полюсов и нуля для системы третьего порядка |
|
Т.- |
Теперь при С, = 0,6 ии„ = 5 мы имеем пару доминирующих полюсов и один нуль, для которого а/(С, озп) = = 0,833. С помощью рис.5.13(a) находим, что относительное перерегулирование составляет 55%. Ожидаемое время установления (по критерию 2% от конечного значения) равно 4 4
_ 0,6-5
= 1,33 с.
Моделирование на компьютере исходной системы третьего порядка дает следующие результаты: пеерегулирование составляет 38%, а время установления равно 1,6 с. Таким образом, влияние третьего полюса T(s) сводится к уменьшению перерегулирования и увеличению времени установления (а. следовательно, вещественным полюсом пренебрегать нельзя).