СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Измерение частотных характеристик

Синусоидальный сигнал можно использовать для измерения частотных характеристик ра­зомкнутой системы управления. На практике это связано с получением графиков зависи­мости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим графи­кам можно определить передаточную функцию разомкнутой системы G/Д/со). Аналогич­ным образом можно получить и частотные характеристики замкнутой системы, после чего определить её передаточную функцию Т(]ы).

Существуют специализированные приборы, позволяющие измерять частотные ха­рактеристики и восстанавливать по их виду выражения для передаточных функций разо­мкнутых и замкнутых систем.

Анализатор 3562А, созданный фирмой Хьюлетт-Паккард, позволяет измерять час­тотные характеристики в диапазоне от 0 до 100 кГц. Средства данного устройства дают возможность не только определять полюсы и нули передаточной функции по экспери­ментально полученным частотным характеристикам, но и строить эти характеристики для введенной пользователем модели системы. Благодаря этому появляется возможность производить сравнение частотных характеристик введённой модели системы с реальны­ми характеристиками, полученными экспериментально (см. рис. 8.10(У)).

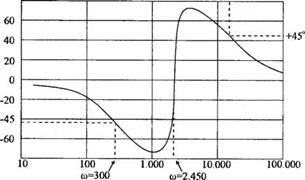
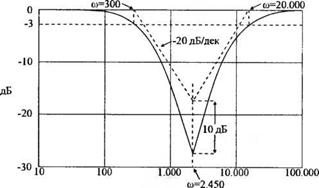
В качестве примера определения передаточной функции по частотным характери­стикам рассмотрим диаграмму Боде, изображённую на рис. 8.23. которая соответствует устойчивой системе, состоящей из резисторов и конденсаторов. Поскольку в диапазоне 100 < со < 1000 амплитудная характеристика имеет наклон -20 дБ/дек, а на частоте со = 300 рад/с фазовый сдвиг равен —45е и амплитудная характеристика равна -3 дБ, мы можем заключить, что один из сомножителей соответствует полюсу р = 300. Далее мож­но сделать вывод, что передаточная функция содержит пару комплексных нулей, соответ­ствующих квадратичному члену с параметрами ^ = 0,16 и со,, = 2450. Это следует из того, что фазовая характеристика резко изменяется почти на + 180°, проходя через значение 0е на частоте со = 2450. Кроме того, после этой частоты наклон амплитудной характеристики изменяется с -20 дБ/дек на +20 дБ/дек. Таким образом, мы уже можем изобразить асимп­тоты амплитудной характеристики, обусловленные полюсом рх и числителем ожидаемой передаточной функции Is) в соответствии с выражением (8.45); эти построения приведе­ны на рис. 8.23(a).

г(д)=(,/со^+(2С/со„>+1 (845)

(s/pi + )(s/p2 +1)

Разность между точной и асимптотической амплитудными характеристиками на час­тоте излома со = 2450 составляет 10 дБ; на основании выражения (8.37) это соответствует значению С, = 0,16. (Сравните частотные характеристики для квадратичного члена в чис­лителе передаточной функции с характеристиками для такого же члена в знаменателе, приведёнными на рис. 8.10. Обратите внимание, что в случае комплексных нулей эти ха­рактеристики просто надо перевернуть «вверх ногами», при этом фазовая характеристика будет изменяться от 0° до +180е, а не до -180°, как при комплексных полюсах.) Поскольку при частотах, превышающих 50000, наклон амплитудной характеристики вновь стано­вится равным 0 дБ/дек, можно заключить, что в передаточной функции появляется второй полюс. Этот полюс равен рг = 20000, т. к. в этой точке амплитудная характеристика на 3 дБ меньше асимптотической, а фазовый сдвиг равен +45° (-90° для первого полюса, +180°

для пары комплексных нулей и —45° для второго полюса). Следовательно, передаточная функция имеет вид:

(s/2450)2 + (0,32/2450>+1

T{s) = -

(s/ЗООн-l)(s/20000+l)

Такие частотные характеристики действительно соответствуют Т-образному че­тырёхполюснику (см. задачи 2.8 и 8.3 и рис. 8.14).