СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Дифференциальные уравнения физических систем

Дифференциальные уравнения, описывающие динамику физической системы, получают­ся на основании фундаментальных физических законов. Этот метод в равной степени при­меним к механическим, электрическим, гидравлическим и термодинамическим системам. Рассмотрим крутящуюся систему пружина масса, изображенную на рис. 2.1, к которой приложен момент TJJ). Предположим также, что упругий элемент (пружина) обладает пренебрежимо малой массой по сравнению с диском. Допустим, что нам необходимо изме­рить момент Ts(t), передаваемый массе т. Поскольку согласно допущению пружина не об­ладает массой, то сумма действующих на нее моментов должна равняться нулю, т. е.

Та (О - Т, (0 = О,

откуда имеем Ts (t) = Ти (/). Мы видим, что внешний момент Ta(t), приложенный к концу пружины, передается сквозь этот упругий элемент. По этой причине мы будем называть момент сквозной переменной. Аналогичным образом, разность угловых скоростей кон­цов упругого элемента равна

ю(0 = ы,(Г) - ша(0-

Эта разность характеризует угловую скорость одного конца упругого элемента относите­льно другого, поэтому мы будем называть ее относительной переменной. Подобные рас­суждения можно сделать и в отношении большинства известных физических переменных (таких как сила, ток, объем, поток и т. п.). В табл. 2.1 приведены сводные данные о сквоз­ных и относительных переменных динамических систем. Информацию относительно Международной системы единиц СИ, применяемой ко многим переменным в этом разде - Л. ле, можно найти на Web-сайте MCS (Modem Control Systems). Например, темпера-

тура в системе СИ измеряется в градусах Кельвина, а длина — в метрах. На этом же Web-сайте приведена таблица соответствий между английской системой единиц и системой СИ. Дифференциальные уравнения линейных динамических элементов с сосре­доточенными параметрами приведены в табл. 2.2. Заметим, что эти уравнения являются идеализированным описанием динамики элементов, т. е. представляют собой всего лишь аппроксимацию их реального поведения (например, когда элемент с распределенными па­раметрами аппроксимируется линейной моделью с сосредоточенными параметрами).

Рис. 2.1

(а) Крутящаяся система пружина-масса;

(б) Упругий элемент

Обозначения:

Сквозные переменные: F— сила, Т — момент, / — ток, Q — объемный расход жидкости, q — тепловой поток.

Относительные переменные: v — поступательная скорость, ш — угловая скорость, и — напряжение, Р — давление, Т— температура.

Индуктивные накопители: L — индуктивность, l/k — обратный коэффициент жесткости, 1 — инертность жидкости.

Емкостные накопители: С — емкость, М—масса, J—момент инерции, С/ —жидкост­ная емкость, С, — тепловая емкость.

Рассеиватели энергии: R — сопротивление, b — вязкое трение, Л— гидравлическое со­противление, R, — тепловое сопротивление.

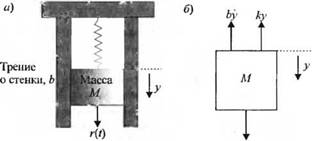
Обозначение v(t) используется как для напряжения в электрических цепях, так и для скорости поступательного движения в механических системах, поэтому смысл этой пере­менной следует понимать в контексте каждого дифференциального уравнения. Для опи­сания механических систем используются законы Ньютона, а для электрических сис­тем — законы Кирхгофа. Например, простой механический амортизатор, изображенный на рис. 2.2(a), описывается вторым законом Ньютона. (Подобное устройство может, на­пример, представлять собой модель автомобильного амортизатора.)

Рис. 2.2

(а) Система пружина-масса с демпфированием.

(б) Условное обозначение

массы и пружины, будет использоваться именно вязкое трение. В соответствии со вторым законом Ньютона, суммируя все силы, действующие на массу М, запишем:

(2.1)

где к — коэффициент упругости пружины, а Ъ — коэффициент трения. Уравнение (2.1) есть дифференциальное уравнение второго порядка с постоянными коэффициентами. Точно так же можно с помощью закона Кирхгофа,-(/) ♦ ^

t) П* Ujc

Рис. 2.3. RLC-цепь

+ C^p + ±]v(t)dt=r(t).

Решение дифференциального уравнения, описывающего динамический процесс, может быть получено классическим методом — путем интегрирования с использовани­ем неопределенных коэффициентов. Например, если груз сместить в начальное положе­ние y(t) = уф) и затем отпустить, то движение такой недодемпфированной системы описывается выражением

XO = ^,e“a|,sin(P1r + ei). (2.3)

Аналогичное решение имеет место для напряжения v(t) RLC-цепи, если она находит­ся под воздействием постоянного тока r(t) = 1:

v(t) = K2e~a2' cos(p2r + 62). (2.4)

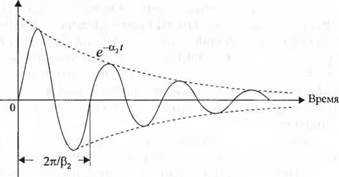
Типичный характер изменения напряжения в недодемпфированой Л1С-цепи показан на рис. 2.4.

Чтобы обнаружить более близкое сходство между дифференциальными уравнения­ми механических и электрических систем, перепишем уравнение (2.1) относительно ско­рости

dy(t)

v(0 = -

dt

В результате получим:

M^-^ + bv{t)+k v(t)dt = r(t). (2.5)

dt о

Сразу же можно отметить эквивалентность уравнений (2.5) и (2.2), только в одном из них переменная v(t) обозначает скорость, а в другом — напряжение. Поэтому данные переменные обычно называют переменными-аналогами, а соответствующие систе­мы — подобными системами. Следовательно, закон изменения скорости будет также иметь вид (2.4), которому соответствует кривая на рис. 2.4. Понятие подобия систем яв­ляется очень полезным и эффективным методом при моделировании. Аналогия между напряжением и скоростью, часто называемая аналогией сила-ток, вполне естественна, поскольку она характеризует связь между подобными сквозными и относительными пе­ременными электрических и механических систем. Однако часто используется и другая аналогия, называемая аналогией сила-напряжение, при которой рассматривается подо­бие скорости и тока.

Подобные системы с одинаковыми решениями можно обнаружить среди электриче­ских, механических, тепловых и гидравлических систем. Наличие таких систем позволяет исследователю распространить решение, полученное для одной системы, на все подоб­ные системы, описываемые аналогичными дифференциальными уравнениями. Следова­тельно, результаты, полученные, скажем, при анализе и синтезе электрических систем, сразу можно применить для представления о поведении гидравлических, тепловых и ме­ханических систем.