СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Анализ моделей в переменных состояния с помощью MATLAB

Анализ систем управления во временной области предполагает задание ее модели в про­странстве состояний:

х=Ах+Вгг и y=Cx + Da. (3.127)

Вектор х характеризует состояние системы, матрица А есть матрица коэффициентов размерности пхп, В — матрица входа размерности пхт, С — матрица выхода размерно­сти рхп, D — матрица обхода размерности рхт. Мы ограничиваемся рассмотрением сис­тем с одним входом и одним выходом, поэтому в данном случае т - р = 1, а_у и г/ являют­ся скалярными переменными (полужирное начертание для них не используется).

Основными элементами модели в пространстве состояний (З. І27) являются вектор х и матрицы (А, В, С, D). Подобное описание как нельзя лучше подходит для использова­ния среды MATLAB, в которой основной рабочей единицей является матрица. В действи­тельности MATLAB охватывает так много различных методов, базирующихся на про­странстве состояний, что рассмотреть их все мы просто не имеем возможности. В данном разделе мы познакомимся с двумя новыми функциями: ss и Isim. Кроме того, мы рассмот­рим функцию ехрт, с помощью которой вычисляется переходная матрица состояния.

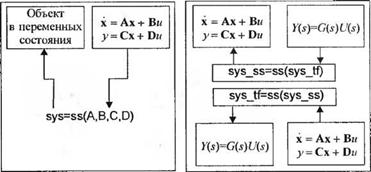
Если задана передаточная функция, то мы можем получить эквивалентную модель системы в переменных состояния и наоборот. Для этого в MATLAB имеются две функ­ции: функция ss позволяет перейти от передаточной функции к представлению системы в пространстве состояний, функция tf выполняет обратную задачу. Смысл этих функций раскрывает рис. 3.28.

Например, рассмотрим систему третьего порядка:

. (3.128,

R(s) s - і &2 + 1 б-V + 6

На рис. 3.29 показано, как с помощью функции ss происходит переход от передаточ­ной функции (3.128) к описанию системы уравнениями (3.127), где

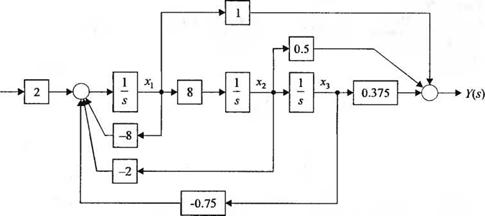
Представление передаточной функции (3.128) в виде модели в переменных состоя­ния приведено на рис. 3.30.

Рис. 3.29

Преобразование передаточной функции (3.128) в форму фазовой переменной в пространстве состояний:

(а) Скрипт MATLAB.

(б) Распечатка результата convert. m

%Преобразование G(s)=(2sA2+8s+6)/(sA3+8sA2+16s+6) %в модель в переменных состояния %

num=[2 8 6]; den=[1 816 6]; sys_tf=tf(num .den); sys_ss=ss(sys_tf)

6) »convert a =

b =

Решение первого из уравнений (3.127) имеет вид:

х(/) =ехр(А/)х(0)+ |ехр[А(ґ-т)]Вг<(т)с/т

Матричная экспоненциальная функция в (3.129) есть переходная матрица состояния Ф(0, т. е. Ф(Г) = exp(Af). Для вычисления переходной матрицы состояния при заданном шаге дискретности по времени используется функция ехрт, как это показано на рис. 3.31. Функция ехрт(А) вычисляет еА. Напротив, функция ехр(А) вычисляет е'1 для каждого элемента ау матрицы А.

Рассмотрим, например, ЛІС-цепь на рис. 3.4, описываемую уравнением состояния

(3.18) , где

Зададимся начальными условиями Х[(0) = х2(0) = 1 и будем считать, что входной сигнал tt(t) = 0. При шаге дискретности 0,2 с вычисленная переходная матрица состояния приведе­на на рис. 3.31. На основании этих данных можно определить состояние системы в момент времени t = 0,2 с:

Временные характеристики системы, заданной передаточной функцией (3.128), мож­но также получить с помощью функции Isim. Эта функция допускает как задание ненуле-

Рис. 3.31

Вычисление переходной матрицы состояния при заданном шаге дискретности At = dt

0.9671 -0.2968 0.1484 0.5219

у(1) — выход в момент t, Т: вектор времени, x(t) — состояние в момент t

t — моменты времени, в которые вычисляется реакция

и = вход

[y, T,x]=lsim(sys, u,t, xO)

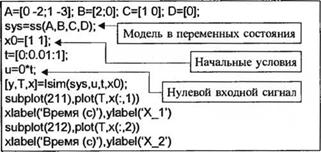
вых начальных условий, так и входной функции, что проиллюстрировано на рис. 3.32. На рис. 3.33 показано, как с помощью функции Isim вычисляется реакция /JLC-цепи. Состоя­ние цепи в момент времени t = 0,2 с, вычисленное с помощью функции Isim, равно *((0,2) = х2(0,2) = 0,6703. Как видим, этот результат полностью совпадает с данными, по­лученными ранее путем умножения переходной матрицы состояния на вектор начальных условий.

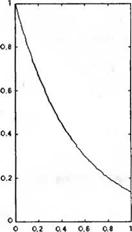
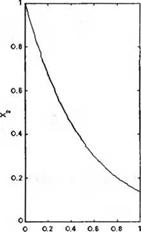
Рис. 3.33

Вычисление с помощью функции Isim временных характеристик при ненулевых начальных условиях и отсутствии входного сигнала