ВЫЧИСЛИТЕЛЬ НЕНАБЛЮДАЕМЫХ КООРДИНАТ ЭЛЕКТРОПРИВОДА
Исходными данными для вычислений, проводимых в вычислителе ненаблюдаемых координат электропривода, являются фазные напряжения на выходе автономного инвертора и фазные токи статора двигателя. Поэтому первая вычислительная операция связана с преобразованием фазных значений наблюдаемых координат в эквивалентные составляющие в координатных осях (а - (3). Преобразования токов выполняются с помощью следующих выражений:
Если измеряемыми координатами являются фазные напряжения на выходе автономного инвертора, то преобразования напряжений выполняются с помощью выражений (1.2).
Если же наблюдаемой координатой является выпрямленное напряжение на выходе звена постоянного тока преобразователя частоты, то для преобразования напряжений используются следующие выражения:
|
|
(2.10)
где Ud - амплитуда выпрямленного напряжения на входе автономного инвертора,
Sa, Sb, Sc - коммутационные функции фазы а, b и с на выходе таблицы переключений силовых электронных модулей автономного инвертора.
Полученные составляющие напряжения и тока статора двигателя позволяют вычислить составляющие потокосцепления статора по следующим выражениям:
(2.11)
^=|(Usp-lsp-Rs)dt,
где Rs - активное сопротивление фазной обмотки статора двигателя.
Имеющейся информации достаточно для вычисления значений модуля (амплитуды вектора) потокосцепления статора и электромагнитного момента двигателя, которые используются в качестве сигналов обратных связей в системе регулирования. Выражение для модуля потокосцепления статора имеет следующий вид:
|
|
(2.12)
Выражение для величины электромагнитного момента двигателя имеет вид:
Мд=^рп(%аІф-^ГІ№),
|
(2.13) |
где рп - число пар полюсов двигателя.
Здесь же целесообразно вычислить тригонометрические функции угла поворота вектора потокосцепления статора |/s относительно оси а, поскольку эта информация потребуется при дальнейших вычислениях.
Для систем DTC с непосредственной индикацией частоты вращения ротора (при использовании вращающегося датчика частоты вращения) этих вычислений достаточно.
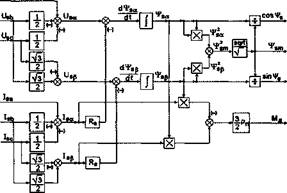
Структурная схема вычислителя потока и момента для таких систем приведена на рис.2.9. Для вычисления функций cos]/s и sin(/s в схеме использованы блоки деления. Здесь и далее на структурных схемах принято, что переменная, вводимая в блок деления по горизонтальной стрелке, является делимым, а переменная, вводимая в блок деления по вертикальной стрелке, является делителем.
|
Рис.2.9. Структурная схема вычислителя потока и момента в системах DTC при наличии датчика скорости. В схеме рис.2.9 блок извлечения квадратного корня обозначен “sqrt”. |
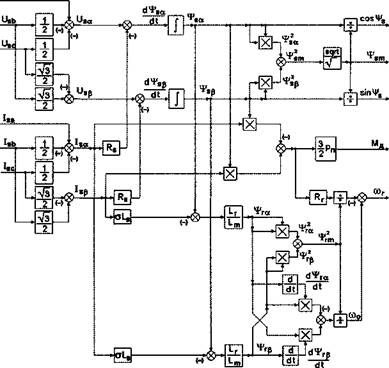
В бездатчиковых системах DTC (без датчика скорости) к приведенным выше вычислениям добавляется следующее. Поскольку частота вращения ротора двигателя входит сомножителем в уравнения электромагнитного равновесия роторной цепи, прежде всего, необходимо определить составляющие вектора потокосцепления ротора в осях (а - (3). Это можно сделать, используя уравнения связи между составляющими токов и потокосцеплений асинхронного двигателя. Выражение в круглых скобках без постоянного коэффициента представляет собой уравнение электромагнитного момента двигателя, выраженное через составляющие тока статора и потокосцепления ротора двигателяСтруктурная схема вычислителя потока, момента и частоты вращения для бездатчиковых систем DTC приведена на рис.2.10.
|
Рис. 2.10. Структурная схема вычислителя потока, момента и частоты вращения ротора двигателя в бездатчиковых системах DTC. |
Необходимо обратить внимание на то, что при вычислении частоты вращения поля статора двигателя в уравнении присутствуют производные составляющих потокосцепления ротора двигателя. При выполнении операции дифференцирования непрерывных функций в численных расчетах всегда появляется вычислительная ошибка. Эта ошибка может повлиять на качество работы всей системы. Частично эта ошибка демпфируется релейным регулятором момента. Тем не менее, при исследовании бездатчиковых систем прямого управления моментом это обстоятельство нельзя упускать из вида.
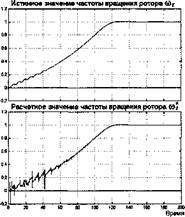
Для примера на рис.2.11, приведены расчетные значения истинной и вычисленной с помощью математической модели кривых изменения частоты вращения при прямом пуске асинхронного двигателя. Расчеты выполнены в системе относительных единиц.
|
Рис. 2.11. Истинное и расчетное значения частоты вращения ротора двигателя при прямом пуске. |
Сопоставление кривых на рис.2.11 показывает, что в диапазоне от 0,4 шном до соном истинная и расчетная характеристики совпадают удовлетворительно. В то же время в зоне малых частот вращения от 0 до 0,4 whom влияние дифференцирующих звеньев проявляется сильно.
В некоторых алгоритмах DTC используется информация о пространственном положении вектора потокосцепления ротора.
Для построения уточненных алгоритмов DTC иногда необходимо знать тригонометрические функции угла поворота вектора потокосцепления статора относительно вектора потокосцепления ротора. Эти вычисления могут быть выполнены по формулам:
cosv|/s_r = cos|/s * cos i|/r + sm v|/s * sin ц/г; sill V|/S_r = sin |/s • COS Щ - COSl|/s * sill |/r.
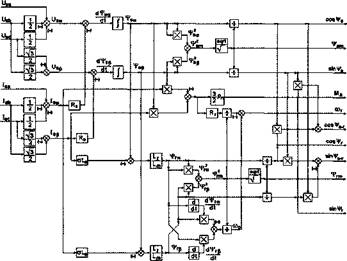
Тогда структурная схема вычислителя потока и момента примет следующий вид:
|
Рис.2.12. Структурная схема вычислителя потока, момента и частоты вращения, содержащая информацию о потоке ротора двигателя в бездатчиковых системах. |