РАСШИРЕНИЕ ИМПУЛЬСА
В разделе 12.3 было показано, что для усиления с линейной частотной модуляцией лазерный импульс необходимо вначале расширить (во времени). В принципе, эту процедуру можно осуществить с помощью одномодового оптического волокна подходящей длины (см. рис. 12.11 и 12.12а). Однако линейное смещение частоты, достигаемое в этом случае (см. рис. 12.136), не может быть полностью компенсировано системой сжатия, состоящей из пары дифракционных решеток (рис. 12.14), что обусловлено наличием в такой системе дисперсии более высокого порядка. Для лазерных импульсов корот-
|
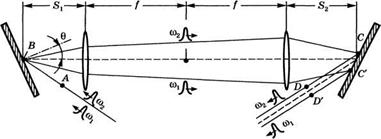
Рис. 12.15 Система расширения импульса, состоящая из двух дифракционных решеток, расположенных во встречно-параллельной конфигурации, и установленного между ними инвертирующего телескопа с увеличением 1:1 |
Кой длительности (суб-пикосекундного диапазона) такая система может обеспечить только частичное сжатие расширенного импульса до его первоначальной формы. Наиболее подходящим решением в этом случае [29] было бы использование системы расширения импульсов, которая также состоит из пары дифракционных решеток, но установленных во встречно-параллельной конфигурации, и инвертирующего телескопа (с увеличением 1:1), установленного между этими решетками, как показано на рис. 12.15 [30]. Для получения требуемой положительной дисперсии групповой задержки две решетки должны быть расположены за телескопом, но в пределах фокуса его линз, т. е. должно выполняться неравенство («х, s2) < f, где f — фокусное расстояние каждой из двух линз телескопа. В этом случае, если принять распространение пучка идеально параксиальным и пренебречь дисперсией в линзах телескопа, то дисперсию групповой задержки можно записать в виде [30]:
ДГЗ = ~ - з С 2 a W - * - *2 >> (12-5-7)
Cfar orcr cos^ 0
Где со — частота волны, d — период решетки, и 0 — угол, показанный на рис. 12.15. Из выражения (12.5.7) видно, что дисперсия групповой задержки оказывается в этом случае положительной. Для объяснения этого результата вновь обратимся к рис. 12.15, на котором плоская волна, приходящая на первую решетку, представлена лучом АВ и состоит из двух синхронных импульсов с частотами со2 и cox, причем со2 > Вследствие дисперсии решетки импульсы проделают пути ABCD и ABCD' соответственно. При этом нетрудно видеть, что задержка, которую испытывает импульс на частоте со2, а именно =ABCD/vg, оказывается теперь больше задержки xdl =ABC'D'/vg
Для импульса на частоте щ. Поскольку со2 > сох, это означает, что дисперсия групповой задержки импульса теперь положительна. Следует заметить, что система, состоящая из двух решеток и телескопа, изображенная на рис. 12.15, также обладает недостатком, связанным с эффектом сноса выходного пучка в поперечном направлении. Величина этого сноса зависит от разницы между частотами различных компонент пучка (например, между лучами CD и C'D'). Для пучков ограниченных размеров это может стать достаточно серьезной проблемой, которую, тем не менее, можно обойти путем переотражения выходного пучка в обратном направлении с помощью плоского зеркала. В этом случае полная дисперсия при двукратном проходе через дифракционные решетки (рис. 12.15) будет иметь удвоенное значение от полученного в выражении (12.5.7).
Чтобы сравнить положительную ДГЗ, рассмотренную в этой схеме (рис. 12.15), с отрицательной ДГЗ, полученной ранее (см. рис. 12.14), необходимо вначале напомнить, что согласно уравнению дифракционной решетки имеем sin 07 - (k/d) = sin 0', где 0* — угол падения на решетку, а 0' — соответствующий угол дифракции. Подставляя это уравнение решетки в выражение (12.5.6) и сравнивая полученный результат с (12.5.7), нетрудно видеть, что при 0' = 0 два выражения становятся идентичными, за исключением знака, и в этом случае можно записать:
(Z^/cos0) = 2f-s1- s2. (12.5.8)
Важно заметить, что это равенство справедливо лишь при идеальных условиях, описанных выше. В этом случае, когда применимо выражение (12.5.8), система расширения импульса, рассмотренная на рис. 12.15, соответствует системе, изображенной на рис. 12.14. Данная ситуация объясняется тем, что телескоп, рассмотренный в одной из схем, формирует изображение первой решетки, которое переносится за пределы второй решетки на воображаемую плоскость, параллельную этой второй решетке. Таким образом, система расширения, изображенная на рис. 12.15, эквивалентна системе с двумя параллельными решетками (отрицательная дисперсия), и при выполнении условия (12.5.8) эта система обладает полностью противоположной дисперсией для всех порядков, по сравнению с системой, показанной на рис. 12.14.
На практике из-за наличия в линзах телескопа дисперсии и различных аберраций система расширения импульса, показанная на рис. 12.15, достаточно хорошо работает с импульсами, длительность которых оказывается больше ~100 фс, при этом коэффициент расширения не превышает нескольких тысяч. Для работы с более короткими импульсами и для достижения более высоких коэффициентов расширения конструкция телескопа (с увеличением 1:1) в описанной выше системе расширения предусматривает использование специальных цилиндрических [31] или сферических [32] зеркал. В частности, использование конфигурации с цилиндрическим зеркалом позволило получить коэффициент расширения более 104, при этом учитывалась дисперсия второго, третьего и четвертого порядков для выбранных соответствующим образом материалов усилительных сред [31].