СЖАТИЕ ИМПУЛЬСА
Схема установки, которая обычно используется для получения сверхкоротких лазерных импульсов, приведена на рис. 12.11. Импульс лазера, работающего в режиме синхронизации мод с достаточно большой пиковой мощностью (на практике относительно скромные значения составляют около Рр = 2 кВт) и большой длительностью импульса (например, хр = 6 пс), пропускается через одномодовое кварцевое оптоволокно подходящей длины (например, Ь = 3 м). Длина волны импульса (например, X = 590 нм) попадает в область положительной дисперсии групповой скорости волокна (обычно в без - дисперсионных волокнах А,< 1,32 мкм). После выхода из волокна импульс коллимируется и проходит через систему двух одинаковых дифракционных решеток, расположенных параллельно друг другу. Наклон этих решеток и расстояние между ними подбирается вполне определенным образом, см. ниже. При подходящих условиях выходной пучок представляет собой импульс света, длительность которого значительно меньше, чем у входного импульса (например, хр = 200 фс) и, следовательно, пиковая мощность выходного импульса оказывается намного больше (например, Рр = 20 кВт). Таким образом, устройство, изображенное на рис. 12.11, позволяет получить очень большой коэффициент сжатия (например, в рассмотренном случае около 30) входного импульса. Более сложные явления, происходящие во время сжатия импульса, будут рассмотрены ниже [21, 22].
Рассмотрим сначала процессы, которые имеют место при распространении импульса в оптическом волокне. Следует напомнить, что вследствие эффекта фазовой самомодуляции световой импульс с равномерным поперечным профилем распределения интенсивности, который распространяется на расстояние г в среде, вызывает в этой среде эффект Керра, обусловленный наличием нелинейного члена (см. выражение 8.6.38), отвечающего за смещение фазы. Однако в оптическом волокне ситуация несколько более сложная, вследствие неравномерного поперечного профиля распределения интенсивности основной моды (ЕНи). В этом случае можно показать, что полный профиль моды испытывает фазовый сдвиг, описываемый следующим выражением [22]:
Л./* ~ + ^ьпо „ ЫьП2Р „
♦&г)-о>£* —г—г, (12.5.1)
Где п0 — показатель преломления в отсутствие поля, п2 — коэффициент нелинейного показателя преломления среды (см. выражение (8.6.23)), Р = Р(*, г) —
6 пс ^^ 25 пс
Дифракционная
Входной Одномодовое Выходной решетка
Импульс оптическое волокно импульс ^/
ДИФрРешеткаН^ Щ///М
Рис. 12.11
Экспериментальная установка для сжатия лазерных импульсов
|
|
|
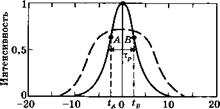
Рис. 12.12 Зависимости от времени (а) интенсивности импульса и (б) частоты импульса при прохождении лазерного пучка через одномодовое оптическое волокно соответствующей длины: Сплошная кривая соответствует случаю отсутствия дисперсии групповой скорости, а штриховая — наличию положительной дисперсии групповой скорости в волокне. |
|
^_____________ 0 Время (пс) Пространство |
 Мощность пучка, распространяющегося по волокну и Ае]^ — определяемая надлежащим образом эффективная область пучка в волокне. Мгновенное значение несущей частоты светового импульса выводится из выражения (12.5.1) и имеет следующий вид:
Мощность пучка, распространяющегося по волокну и Ае]^ — определяемая надлежащим образом эффективная область пучка в волокне. Мгновенное значение несущей частоты светового импульса выводится из выражения (12.5.1) и имеет следующий вид:
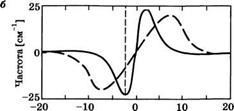
Откуда нетрудно видеть, что она линейно зависит от производной мгновенной мощности Р излучения по времени, взятой с обратным знаком. Таким образом, для импульса колоколообразной формы, показанного на рис. 12.12а, несущая частота будет изменяться со временем так, как показано сплошной линией на рис. 12.126. Заметим, что вблизи пика импульса, т. е. в той области, где зависимость от времени можно описать параболой, мгновенное значение несущей частоты линейно растет со временем (т. е. говорят, что импульс обладает положительным смещением частоты или положительным чирпом). Следует заметить также, что смещение частоты становится отрицательным на крыльях профиля распределения, т. е. при t<tA или £ > на рис. 12.126.
Рассмотренная выше физическая картина не дает полного представления о том, что происходит на самом деле в волокне, поскольку при рассмотрении не учитывалась положительная дисперсия групповой скорости (ДГС). При отсутствии ДГС форма светового импульса, распространяющегося по волокну, не изменяется, т. е. амплитуда поля остается функцией от переменной (г - и^£), где иё — групповая скорость (см. приложение Ж). При этом зависимость интенсивности импульса от координаты г в заданный момент времени остается такой же, что и на рис. 12.12, в предположении, что положительное направление оси изменяется на противоположное и масштаб времени умножается на величину иё. Это означает, что, например, точка А на рис. 12.12а
в действительности находится на переднем фронте импульса, в то время как точка В — на заднем фронте. Заметим теперь, что в соответствии с рис. 12.126, несущая частота импульса о> вблизи точки А будет ниже, чем в точке С, где частота примерно равна со1(. С другой стороны, несущая частота импульса вблизи точки В будет выше, чем в точке С.
Предположим теперь, что волокно имеет положительную ДГС. При этом часть импульса, которая находится в окрестностях точки А, будет двигаться быстрее, чем соответствующая часть импульса вблизи точки С, а последняя, в свою очередь, будет двигаться быстрее, чем область импульса вблизи точки В. Это означает, что при распространении по волокну центральная часть импульса будет растягиваться. При помощи аналогичных рассуждений можно показать, что фронты импульса будут не растягиваться, а обостряться, поскольку в этих областях смещение частоты оказывается отрицательным. Следовательно, при рассмотрении положительной ДГС истинная форма импульса как функция времени в данной точке г будет такой, как показано на рис. 12.12а штриховой кривой. Соответствующая зависимость смещения частоты показана штриховой кривой на рис. 12.126. Из рис. 12.12а видно, что вследствие уширения, обусловленного дисперсией групповой скорости, максимальная интенсивность импульса, изображенного штриховой кривой, оказывается меньше, чем для сплошной кривой. Заметим также, что поскольку параболическая зависимость импульса распространяется теперь на более широкую область вблизи пика, положительное линейное смещение частоты распространяется на большую часть импульса.
|
0,3 0,2 0,1 0 |
![]()
|
Время, пс |
 Установив эти общие особенности взаимодействия процессов фазовой са - момодуляции и дисперсии групповой скорости, можно показать, что если
Установив эти общие особенности взаимодействия процессов фазовой са - момодуляции и дисперсии групповой скорости, можно показать, что если
В
18 И м
К 5
О
И 0
О) 25
Д
К
|
10 |
![]() _|____ I____ 1_
_|____ I____ 1_
|
| 1 1 1 1 |
Т---- |
Л 10 И 8 ч |
■ ' “ |
■ ■ |
|
-------- 1-. |
ГХ-------- 1------- 1-------- 1------- 1------- 1------ |
К ^ е Ё|б ф £ Я 0 |
||
|
-20 -10 0 10 20 Время, пс |
|
-Г”“1 ^ 2 ' 8 К у ц О) В 2 0 §1 ° I |
|
-25 |
|
-20 -10 |
|
0 Время, пс |
|
10 |
|
20 |
|
-10 |
|
-5 0 5 Время, пс |
|
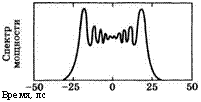
Рис. 12.13 Графики (а) расчетных значений самоуширения и (б) фазовой самомодуляции исходного импульса длительностью 6 пс после распространения в одномодовом волокне с положительной дисперсией групповой скорости на расстояние 30 м; (в) спектр выходного импульса; (г) форма сжатого импульса после прохождения оптической системы с отрицательной дисперсией групповой скорости. (Согласно работе [21].) |
Длина волокна достаточно большая, то на выходе волокна форма импульса и частота будут изменяться во времени так, как изображено на рис. 12.13а и б. Заметим, в частности, что для импульса, уширенного до т'р = 23 пс, положительное смещение частоты оказывается линейным во времени на протяжении большей части импульса. Соответствующий спектр мощности этого импульса приведен на рис. 12.13в, откуда видно, что благодаря сильной фазовой само - модуляции, имеющей место в случае таких маленьких пучков в волокне (диаметр сердцевины волокна для условий, изображенных на рис. 12.13, составляет <2 = 4мкм), ширина спектра (Ау^ =50 см-1) выходного импульса заметно превышает первоначальную ширину спектра импульса на входе в волокно, которая определялась обратной длительностью импульса, т. е. Аь = 0,45/тр = 2,5 см-1 (для рассмотренного случая тр = 6 пс). Это означает, что ширина полосы на выходе в основном определяется фазовой модуляцией, а не длительностью его огибающей.
Предположим теперь, что импульс на рис. 12.13а и 12.136 пропускается через среду с отрицательной дисперсией групповой скорости. Используя те же рассуждения, что и в связи с рис. 12.12, можно показать, что область импульса вблизи точки А будет двигаться медленнее, чем вблизи точки С, а последняя, в свою очередь, будет двигаться медленнее, чем область импульса вблизи точки В. Это означает, что импульс при распространении по волокну будет сжиматься. Предположим теперь, что дисперсия групповой скорости среды помимо того, что она отрицательна, не зависит также от частоты. Согласно выражению (8.6.27), это означает, что дисперсия групповой задержки будет также отрицательной и не будет зависеть от частоты, таким образом, величина тё будет линейно уменьшаться с частотой. Поскольку смещение частоты импульса увеличивается линейно со временем (см. рис. 12.136), все точки импульса на рис. 12.13а будут сжиматься вместе в одно и то же время при определенном значении дисперсии групповой задержки. Это оптимальное значение дисперсии можно определить с помощью выражения (8.6.31) и записать ввиде:
Дсо^, - Тр, (12.5.3)
Лох,
Где Асо'ь =2яАу^ — полное смещение частоты импульса на рис. 12.136, и т'р — длительность уширенного импульса на рис. 12.13а. Однако следует заметить, что описанный механизм сжатия одновременно всех точек импульса означает переход частотной модуляции импульса в амплитудную модуляцию. Поскольку в процессе этой операции спектр импульса сохраняется (т. е. он по - прежнему остается таким же, как на рис. 12.13в), длительность сжатого импульса тр должна быть приблизительно равна (по крайней мере, не меньше) обратной ширине полосы спектра, т. е. тр = 1/Ау^ =0,75пс. Учитывая, что первоначальная длительность импульса тр (на входе в волокно) была равна -6 пс (см. рис. 12.11а), данный результат означает, что было достигнуто существенное сжатие импульса[78].
<ІС02
Следует заметить, что приведенное выше эвристическое описание основывалось на допущении, что импульс с частотным смещением может быть разделен на отдельные отрезки времени с различными несущими частотами. Хотя данная идея в принципе верна и позволяет дать простое описание явлений, более подробное рассмотрение этого подхода привело бы к некоторым концептуальным трудностям. Однако корректные аналитические выкладки в данном случае оказываются достаточно прямолинейными, хотя при этом физика процесса становится более сложной и далекой от интуитивного представления. Для аналитического представления достаточно вычислить Фурье - образы Ею(о)) импульсов, изображенных на рис. 12.13а и12.136 и умножить их (в частотной области) на пропускание £(о>) среды с отрицательной дисперсией групповой задержки. При этом результирующий импульс (во временной области) получают осуществлением обратного Фурье-преобразования произведения Е(со)1(со). Заметим, что в среде без потерь пропускание £(«>) представляет собой в чистом виде фазовый член, определяемый выражением:
*(ю) = ехр(-уф), (12.5.4)
Где ф = ф(со). Если среда имеет постоянную дисперсию групповой задержки, то величину ф(со) можно разложить в ряд Тейлора относительно центральной несущей частоты соь (с точностью до квадратичного члена):
Ф(со) = ф(о1,)+^^ (12.5.5)
Где (с/ф/ско)^ — групповая задержка, а (й2ф/с/со2)а£ — дисперсия групповой задержки. Подставляя данное разложение в выражение (12.5.4) и производя обратное Фурье-преобразование произведения Е((оЩ(о), находим, что если величина (^ф/Ло2)^ отрицательна и удовлетворяет условию (12.5.3), то имеет место оптимальное сжатие импульса. Оптимально сжатый импульс, вычисленный таким образом, показан на рис. 12.13г. Длительность этого импульса имеет порядок т" =0,6пс, что является более правильным, если
|
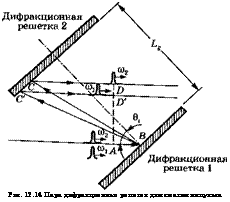
Рис. 12.14 Пара дифракционных решеток для сжатия импульса |
 Сравнивать с приближенным значением (0,75 пс), полученным выше.
Сравнивать с приближенным значением (0,75 пс), полученным выше.
Теперь осталось найти подходящую оптическую систему, которая может обеспечить необходимую отрицательную дисперсию групповой задержки ДГЗ = Отрицательная ДГЗ под
Разумевает, что групповая задержка должна уменьшаться с увеличением частоты о. Как уже обсуждалось в разделе 8.6.4.4, одна из таких систем состоит из призменной пары, приведенной на рис. 8.26. Другая система представляет собой пару параллельных одинаковых дифракционных решеток, изображенных на рис. 12.11 [23]. Для
разъяснения этого момента следует обратиться к рис. 12.14, где показана плоская волна, описываемая лучом АВ, падающим на решетку 1. Волна распространяется под углом 0* к нормали решетки. Предположим, что падающая волна состоит из двух синхронных импульсов с частотами со2 и со19 причем а>2 > ©!. Вследствие дисперсии решетки импульсы проделают пути АВСБ ыАВС'и соответственно. При этом нетрудно видеть, что задержка, которую испытывает импульс на частоте со2, а именно = АВСБ/иё, оказывается меньше задержки хйх =АВС'В'/ие для импульса на частоте ©х. Поскольку со2 > ©!, это означает, что дисперсия групповой задержки импульса отрицательна. С помощью подробных расчетов можно показать, что дисперсионное уравнение запишется в виде [23]:
Ттро _ ^ Ф _ 4П2с____________ 1_________ т /•! л К
<*со2 со3с?2 {[1-[вт0* ~(к/с1)]2}3/2 ш% ( •
Где со — частота волны, X — ее длина, (I — период решетки, а Ьё — расстояние между решетками. При этом знак минус в правой части выражения (12.5.6) показывает, что дисперсия групповой задержки отрицательна. Следует заметить, что величину дисперсии можно менять, изменяя Ьё и (или) угол падения 0*.
Важно также отметить, что система из двух решеток, изображенная на рис. 12.14, обладает определенным недостатком, связанным с эффектом «сноса» выходного пучка в поперечном направлении. Величина этого сноса зависит от разницы между частотами различных компонент пучка (например, между лучами С£> и С'Б'). Для пучков ограниченных размеров это может стать достаточно серьезной проблемой, которую, тем не менее, можно обойти путем переотражения выходного пучка в обратном направлении с помощью плоского зеркала. В этом случае полная дисперсия при двукратном проходе через дифракционные решетки будет иметь удвоенное значение от полученного в выражении (12.5.6).
Система, показанная на рис. 12.11, применялась для осуществления сжатия как пикосекундных, так и фемтосекундных лазерных импульсов при самых различных условиях [24]. Например, импульсы длительностью ~6 пс (и пиковой мощностью -2 кВт) от лазера на красителе с синхронной накачкой и синхронизацией мод были сжаты с использованием оптоволокна длиной 3 м до длительности около 200 фс (Рр = 20 кВт). Эти импульсы были повторно сжаты до длительности 90 фс с помощью аналогичной системы (рис. 12.11), в которой использовалось волокно длиной 55 см. Наиболее интересным результатом является сжатие лазерных импульсов длительностью 50 фс от лазера на красителе с синхронизацией мод на сталкивающихся импульсах до длительности -6 фс, при этом использовалось волокно длиной 10 мм [25]. Для получения импульсов такой малой длительности использовался подход, при котором дисперсия групповой задержки второго порядка (ДГЗ = (б?2ф/с/со2)^) и дисперсия групповой задержки третьего порядка (ТДГЗ = (^3ф/^со3)СОь ) компенсировались за счет использования двух последовательных пар дифракционных решеток (каждая из которых приведена на рис. 12.14) и системы из четырех призм, изображенных на рис. 8.26. Действительно, дисперсии третьего порядка в этих двух системах сжатия имеют разные знаки и, следовательно, компенсируются.
Ограничения, имеющие место в системах сжатия на оптоволокне (рис. 12.11), обусловлены малым диаметром сердцевины волокна (й = 5 мкм). В связи с этим энергия лазерного импульса, которая может быть введена в волокно, ограничена достаточно низкими значениями (~10 нДж). В последнее время разрабатывается схема для формирования широкополосного БРМ-сиектра (спектра фазовой самомодуляции), в которой используется пустотелое оптическое волокно, наполненное благородными газами (Кг, Аг) под высоким давлением (1-3 атм.)[26]. Таким образом, имея внутренний диаметр 150- 300 мкм для пустотелого волокна, можно ввести в такое волокно импульсы с достаточно большей энергией (~2 мДж). При использовании такого волокна длиной около 1 м обеспечивается широкий &РМ-спектр (~200 нм) с входными импульсами фемтосекундной длительности (20-150 фс). С помощью специально разработанной двухпризменной системы, используемой в двухпроходной конфигурации, и за счет двух отражений от специального зеркала с линейной частотной модуляцией [27] исходные лазерные импульсы длительностью 20 фс от лазера на титан-сапфире с синхронизацией мод были сжаты до длительности -4,5 фс [28]. Эти сжатые импульсы состоят примерно из 1,5 циклов несущей частоты и в настоящее время являются наиболее короткими, при этом энергия таких импульсов оказывается достаточно большой (около 100 мкДж).