ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

СМЕШИВАНИЕ В ОСЕВОМ НАПРАВЛЕНИИ

Как уже отмечалось (см. разд. 4.1), для непрерывно действующих смесителей особое значение име­ет величина сглаживающей способности. При описании осевого смешивания воспользуемся результа­тами работы [27]. Экспериментальные исследования показывают, что большинство непрерывно дейст­вующих смесителей обладают сглаживающей способностью по отношению к флуктуациям входных пи­тающих потоков, и это позволяет комплектовать смесительные установки более дешевыми и надежными в работе питателями объемного принципа действия, например шлюзовыми, шнековыми, ленточными, та­рельчатыми.

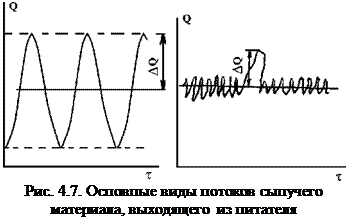
Возможны следующие три вида потоков сыпучего материала, выходящего из питателя (рис. 4.7): а - изменение мгновенной весовой производительности Q питателя носит периодический характер, при­чем средняя весовая производительность Q постоянна во времени т; б - колебания мгновенной весо­вой производительности носят случайный характер и происходят с большой частотой около постоян­ной средней весовой производительности; в - изменение мгновенной производительности носит перио­дический или случайный характер, но среднее значение Q колеблется во времени с малой частотой.

а) б) в)

Во всех трех случаях в каждый момент в смеситель поступают компоненты в соотношении, отлич­ном от необходимого. Однако отклонения в питающих потоках первых двух видов можно сгладить в смесителе, а питатели, дающие поток третьего вида, непригодны для непрерывно-действующих смеси­телей.

Сглаживающая способность барабанного смесителя, зависящая от продольного смешивания, опре­деляется объемом материала, находящегося в барабане, и характером его движения через смеситель.

Для описания процесса осевого смешивания частиц может быть использована диффузионная мо­дель [26], согласно которой изменение концентрации ключевого компонента во времени и вдоль оси барабана описывается следующим уравнением:

где С - концентрация ключевого компонента; x - продолжительность процесса; D - коэффициент про­дольного перемешивания; х - расстояние вдоль оси барабана от места ввода ключевого компонента до распределительного сечения; w - линейная скорость потока материала через барабан.

При допущении о том, что во времени D и w постоянны, использовано следующее решение урав­нения (4.46):

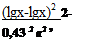
(4.47)

где С{х) - мгновенная концентрация ключевого компонента, импульсно введенного в аппарат, при про­ходе материала через определенное поперечное сечение; G - количество мгновенно введенного ключе - вого компонента; Q - весовой расход материала через барабан; о - относительная дисперсия времени пребывания частиц ключевого компонента, импульсно вводимого в аппарат; х - среднее время пребы­вания частиц материала в аппарате.

Для определения численных значений х и о предложены следующие формулы:

х = —; а2=^, (4.48)

где L - длина барабана.

Возмущение во входном потоке заменено "ступенькой" шириной хв и высотой 67хв. При этом вели­чина относительной дисперсии времени пребывания частиц в аппарате определялась по формуле

о2=а2+^- (4.49)

12х2

Подставив выражения (4.49) в уравнение (4.47), с учетом формулы (4.48) получим [26]:

По уравнению (4.50) можно рассчитать длину барабана Ц необходимую для сглаживания входных возмущений, поскольку максимальное значение концентрации ключевого компонента в потоке на рас­стоянии L от места ввода достигается при х = х. Для случая, когда величина максимального отклонения концентрации на входе равна АС^Х, а на выходе А, получена следующая формула для определения длины барабана, обеспечивающей сглаживание АС^Х до АС^Х :

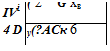(4.51)

Как видно из формулы (4.51), при прочих равных условиях необходимая длина барабана зависит только от значения коэффициента осевого смешивания Д для расчета которого используется следую­щая эмпирическая формула [27]:

D= Кa0’9 d1’9 Ф1’1 ф0’25, (4.52)

где К - коэффициент, зависящий от физико-механических свойств материала (для алюмосиликатного катализатора сферической формы с диаметром частиц 3-4 мм К= 0,8-10^; для крошки капроновой смолы, имеющей цилиндрическую форму высотой 7 мм и диаметром 2 мм, К= 0,2-10 ; для кварцевого
песка крунностью частиц 200 - 500 мкм К=1,2-10 3); w - угловая скорость вращения барабана, 1/с; cl - диаметр барабана; ф - коэффициент заполнения барабана материалом.

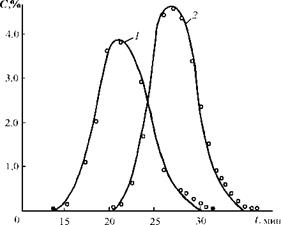
В работе [27] приводятся результаты сравнения экспериментальных и расчетных данных (рис. 4.8). Опыты проводились на лабораторных барабанах с диаметрами 0,145 и 0,2 м и длиной 0,4; 0,6; 1 м. Ско­рость вращения изменялась от 15 до 70 об/мин. В качестве основного материала в барабан вводим от 4 до 8 г/с кварцевого песка с частицами диаметром 200 - 500 мкм. В качестве ключевого компонента ис­пользовали хлористый натрий той же крупности, что и основной материал.

Методика проведения опытов следующая. В установившийся поток основного материала в момент времени т = 0 мгновенно вводили ключевой компонент в количестве G, на выходе из барабана через определенные промежутки времени отбирались 40 - 60 проб для определения концентрации ключевого компонента. По этой же методике были проведены опыты с вводом GT ключевого компонента в основ­ной поток в течение времени тв. Коэффициент заполнения барабана материалом изменялся от 0,3 до 0,5.

(2)-

Моделирование процесса смешивания в циркуляционных смесителях непрерывного действия сопря­жено с рядом сложностей, связанных с тем, что материал перемещается не только в поперечном сечеиии смесителя, но и вдоль его оси. Характер этого движения зависит как от конструкции смесителя, так и от его режимных параметров. В то же время для многих тииов циркуляционных смесителей непрерывного действия (барабанные, вибрационные, вибровращательные и др.) можно выделить ряд общих закономер­ностей: более интенсивное смешивание в радиальном направлений при достаточно ярко выраженном цир­куляционном движении материала; уменьшение степени заполнения поперечного сечения смесителя ма­териалом при движении от области загрузки к области разгрузки наряду с увеличением скорости осевого движения.

Сказанное выше позволяет сделать предположение о том, что для циркуляционных смесителей не­прерывного действия может быть разработана единая математическая модель процесса смешивания [28].

Несмотря на то, что детерминированно-стохастические модели для периодического процесса сме­шивания не учитывают движения компонентов вдоль оси смесителя, они могут быть положены в осно­ву описания процесса непрерывного смешивания, поскольку в осевом движении сыпучего материала наблюдается достаточно ярко выраженный детерминированно-стохастический характер [29].

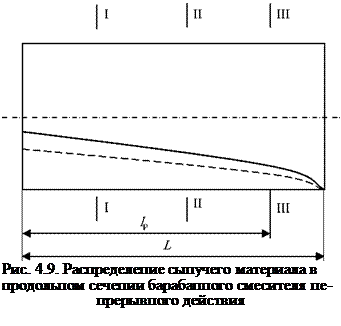
Для барабанного смесителя непрерывного действия продольное сечение барабана, частично запол­ненного смешиваемыми компонентами, изображено на рис. 4.9. Как видно из рисунка, количество ма­териала убывает в направлении от области загрузки барабана (слева) до области разгрузки (справа). Ес­ли провести три поперечных сечения I - I, II - II, III - III, то очевидно, что площадь, занятая циркуляци­онным контуром материала в сечении 1-І, будет наибольшей, а площадь в сечении III - III наимень­шей. Учитывая сказанное, при моделировании процесса смешивания в барабанном смесителе непре­рывного действия невозможно рассматривать процесс, проходящий в фиксированном циркуляционном контуре. Необходимо учитывать как факт перемещения материала вдоль оси барабана, так и факт уменьшения площади, запятой материалом в поперечном сечении смесителя [30].

С учетом того, что по мере удаления от области загрузки барабана количество материала в попе­речных сечениях убывает, скорость продвижения материала в осевом направлении будет возрастать,

поскольку выполняется условие неразрывности потока. Таким образом, имеет место закономерность, связывающая количество сыпучего материала в поперечном сечении барабана с его скоростью продви­жения в осевом направлении.

Для определения объема материала, участвующего на каждом переходе в процессе смешивания, не­обходимо также установить количество материала, находящегося в барабанном смесителе [31]. В каче­стве исходных данных для определения этого параметра необходимо использовать площади, занятые циркуляционным контуром в области загрузки и области разгрузки барабана.

Если закон распределения материала вдоль оси барабана имеет линейный характер, то объем мате­риала, находящегося в барабане, можно определить по зависимости:

V={FH+FK)L/2, (4.53)

где FH и FK — площади, занятые циркуляционным контуром в торцевых сечениях барабана; L - длина барабана.

В рассматриваемой модели процесса смешивания используется относительная скорость осевого движения. Для этого определяется, какую долю от суммарного пребывания в смесителе составляет вре­мя цикла в первом сечении. Поскольку нам известна площадь, занятая материалом в месте загрузки сы­пучего материала FH (в сечении і = 1) и, следовательно, время цикла тц „ то эта доля может быть най­дена следующим образом:

$ = *ц (4.54)

где Тп - время пребывания частицы в барабанном смесителе.

За время тц>/ материал перемещается на определенное расстояние в осевом направлении. Можно

считать, что в данном переходе участвует определенный объем сыпучего материала. Он может быть рассчитан как доля от суммарного объема материала, находящегося в барабанном смесителе:

Ц= Si V. (4.55)

Этот элементарный объем может быть определен как произведение площади циркуляционного кон­тура Fj (при i= 1 имеемFj = FH) на длину элементарного участка в осевом направлении. Таким образом, расстояние, на которое переместится слой материала в осевом направлении барабана на данном участке за время тц „ определяется зависимостью:

h = VJF;.

При переходе на следующий участок необходимо учесть уменьшение площади поперечного сече­ния барабана, запятой материалом, с учетом того, что она изменяется от FH до FK по линейному закону. При изменении расстояния на 7У площадь, занятая материалом, FI+l может быть рассчитана исходя из предыдущего значения Ft:

FM= F1-(Fu-FK)l1/L.

После расчета новой площади, занятой сыпучим материалом в поперечном сечении барабана, про­изводится пересчет конфигурации контура и соответствующего значения времени цикла тц ;+, и далее

по зависимостям (4.54) - (4.57), принимая вместо і значение /’+ 1.

Таким образом, процесс движения в барабанном смесителе непрерывного действия представлен нами дискретным в пространстве и времени [32]. В связи с этим процесс смешивание - сегрегация мож­но считать аналогичным периодическому, но переход на каждый следующий участок должен учитывать изменение конфигурации циркуляционного контура, связанное с уменьшением площади, занятой мате­риалом в поперечном сечении барабана.

Расчеты по математической модели непрерывного процесса смешивания показывают, что наблю­даются небольшие колебания времени цикла тц при продвижении к ссыпающему краю барабана. Диа­пазон изменения времени цикла весьма незначителен и не превышает 2.. .3 %.

Имеющаяся структура распределения компонентов по подслоям циркуляционного контура должна быть сохранена при уменьшении площади, рассчитанной по зависимости (4.57), на каждом переходе. На каждом переходе л?, для случая трехкомпонентной смеси, концентрация ключевых компонентов С и Сі есть функция радиуса, определяющего положение подслоя, т. е. = /)'(/?); СІ'”1 = f-R), где R изменяет­ся от радиуса центра циркуляции R до радиуса барабана /?,. Вследствие того, что распределение клю­чевых компонентов по объему смеси не одинаково, функции fx и f2 различны.

Концентрации ключевых компонентов в пределах каждого подслоя определяются зависимостями:

(4.58)

(4.58) где і - номер ПОДСЛОЯ, 7 = 1, ..., 72-1 .

При этом вне зависимости от того, изменилось или нет число подслоев, функции, описывающие распределение концентраций ключевых компонентов в поднимающемся слое, должны оставаться оди­наковыми, изменяются ЛИШЬ величины, определяющие расположение подслоев, Т. е. Д, 7 = 1, ..., 72.

Средние концентрации каждого из ключевых компонентов в объеме смеси должны оставаться посто­янными. Они определяются зависимостями:

При этом возможны два варианта.

1. Число подслоев не уменьшилось, изменилась лишь их толщина. Рассмотрим, в каком случае воз­можно возникновение этого варианта. Как было показано выше, при делении скатывающегося слоя на подслои по зависимости (4.21) предусматривается использование целой части числа в качества количе­ства подслоев, а оставшаяся дробная часть равномерно распределяется между подслоями. Величина этой дробной части может быть маленькой и тогда к объему каждого из подслоев добавится очень не­большая величина. В случае, если величина дробной части будет достаточно большой, при ее разделе по подслоям в каждый из них добавится довольно большой объем. Как было отмечено ранее, величина добавленного объема в каждый из подслоев будет пропорциональной объему подслоя. Если дробная
часть была достаточно большой, то при изменении площади, занятой материалом в поперечном сечении барабана, разбивка циркуляционного контура на подслои может привести не к уменьшению числа под­слоев, а к уменьшению величины этой дробной части. С учетом того, что объемы подслоев изменяются пропорционально, достаточно сохранить имеющуюся до пересчета структуру распределения ключевых компонентов по подслоям циркуляционного контура.

2. В результате изменения площади, занятой сыпучим материалом в поперечном сечении барабана, произошло уменьшение числа подслоев. В этом случае необходимо пересчитать концентрации ключе­вых компонентов по вновь образованным подслоям циркуляционного контура с сохранением имевшей­ся структуры распределения.

Поскольку изменение площади, занятой циркуляционным контуром вдоль оси барабана, происхо­дит монотонно и может быть описано прямой с небольшим углом наклона к горизонту, а время цикла гораздо меньше времени пребывании частицы в барабане, максимальное уменьшение числа подслоев не может быть больше единицы. Пусть до пересчета параметров циркуляционного контура имелось п под­слоев, в результате пересчета стало п - 1 подслоев. Тогда ключевые компоненты этого "утерянного" подслоя должны быть распределены между оставшимися с сохранением имеющейся структуры распре­деления. Каждый вновь образованный подслой должен содержать частицы одноименного (до пересчета) подслоя, а также часть частиц следующего по порядку подслоя [33]. Изменение количества подслоев составит:

г=п/(п-1). (4.62)

Для случая трехкомпонентной смеси концентрация ключевых компонентов в любом подслое после уменьшения числа подслоев составит:

Cl^ = (co1il’m)(r+i(l-r))+ СО^1’^ г; (4.63)

= (с02(7>) (г+У( 1 - г)) + Ой2{м’ш) і{г-1))/ г, (4.64)

где і - номер подслоя, 7 = 1,..., 72-1; и - концентрации первого и второго компонента в і-м

подслое до изменения числа подслоев; т - номер перехода.

За один переход принимается промежуток времени, за который самый маленький подслой соверша­ет полный оборот вокруг центра циркуляции.

При моделировании процесса смешивания сыпучих материалов в барабанном смесителе непрерыв­ного действия необходимо учитывать факт неравномерного распределения скоростей движения в осе­вом направлении барабана по толщине скатывающегося слоя.

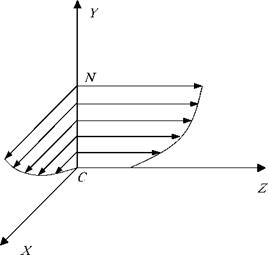
Схема распределения скоростей движения частиц в скатывающемся слое в поперечном и продоль­ном сечениях барабана для случая 5 подслоев представлена на рис. 4.10. Схема распределения скоро­стей по подслоям в поперечном сечении барабана изображена в плоскости XOY. Точка С соответствует положению центра циркуляции, а точка N - открытой поверхности барабана. В плоскости YOZ пред­ставлена схема изменения скоростей движения частиц в осевом сечении барабана. Скорость продвиже­ния частиц, расположенных в районе центра циркуляции (в точке С), в этом случае, в отличие от скоро­сти продвижения в поперечном сечении барабана, ненулевая. Как видно из рисунка, законы изменения скоростей носят нелинейный характер.

С учетом того, что скорости движения в осевом сечении барабана по толщине скатывающего слоя не одинаковы, различен и путь, который проходят частицы сыпучего материала вдоль оси барабана за равные промежутки времени.

Рис. 4.10. Схема распределепия скоростей в скатывающемся слое в продольпом и поперечпом се-

чепиях барабапа

Как показали результаты численных экспериментов, линия, соответствующая положению коорди­нат центра тяжести циркуляционного контура вдоль оси барабана, имеет меньший наклон к горизонту, чем линия, соответствующая открытой поверхности материала. Корректность полученных результатов подтверждена экспериментально на плоской модели смесителя барабанного типа. На рис. 4.9 линия, об­разованная центрами тяжести сечений, занятых сыпучим материалом, показана пунктиром, а линия от­крытой поверхности - сплошная.

Именно разница в величинах углов наклона этих линий к горизонту приводит к различию скоростей продвижения частиц сыпучего материала в осевом направлении для различных подслоев циркуляцион­ного контура.

Результаты изменения времени цикла позволяют сделать вывод о том, что для синхронизации вре­мени одного перехода и количества материала, участвующего в процессе смешивания на каждом пере­ходе, в качестве времени цикла на любом переходе следует принять этот параметр, соответствующий участку, расположенному в непосредственной близости от ссыпающего края барабана. При этом будут устранены некоторые колебания этого значения, вызванные искусственным характером разбиения цир­куляционного контура на подслои с использованием зависимости (4.21).

Использование этого подхода позволит утверждать, что на каждом участке в процессе одного пере­хода будут участвовать одинаковые объемы сыпучего материала. Однако длины участков при переходе от области загрузки барабана к области разгрузки будут увеличиваться пропорционально уменьшению площади, занятой материалом в поперечном сечении, и увеличению скорости осевого движения частиц. Тем самым будут соблюдаться условия неразрывности потока в любом поперечном сечении барабана и сохранения объема материала на любом участке барабана.

С учетом указанного подхода изменятся зависимости, определяющие распределение концентраций компонентов смеси по подслоям циркуляционного контура. Рассмотрим эти изменения для случая трех­компонентной смеси, вероятности перехода которых располагаются следующим образом:

Л>1,3 > Я)2 3 > Р012 .

На любой фазе перехода частица компонента, участвующего в обмене и более склонного к сегрега­ции по отношению к другому компоненту, участвующему в обмене, может либо перейти в соседний подслой, расположенный ближе к центру циркуляции, либо остаться в своем подслое (за исключением последнего подслоя п).

Рассмотрим первую фазу перехода первого компонента в подслой, расположенный ближе к центру циркуляции, с последующим вытеснением из него третьего компонента. Вероятность перехода Pt первого компонента из подслоя і в подслой і + 1 на данной фазе перехода в момент времени т = тхц равна:

(4.65)

где /Wj з - вероятность перехода первого компонента в подслой, содержащий только третий компонент

при нулевой концентрации в нем первого компонента; С2^+1лз_1^ - концентрации компонентов

1, 2 соответственно в подслое і + 1 в момент времени т = (/н-і)тц; т= 1,2,1, к- суммарное число пере­ходов при расчете по математической модели процесса.

Время, за которое частица может совершить полный цикл циркуляции тц, может быть определено, как сумма времени пребывания частицы в поднимающемся слое и времени пребывания в скатываю­щемся слое. Оно принимается равным значению, соответствующему участку, расположенному в непо­средственной близости от разгрузочного края барабана, т. е. усредненному значению [35].

Концентрация первого компонента в подслое і после первой фазы перехода будет равна:

где Ф - объем подслоя У; ф) - объем первого компонента, содержащегося в подслое і перед

этой фазой перехода; Ф'к] - объем компонента 1, перешедшего из подслоя У- 1, кото­

рый расположен ближе к обечайке барабана и непосредственно контактирует с подслоем У; р^(і, і+,т) ^,п, харакхЄрИЗуЄХ количество компонента 1, перешедшего из подслоя У в подслой і +1

на данной фазе перехода; - усредненное значение объема последнего подслоя, соответствующего участку, расположенному вблизи ссыпающего края барабана.

Расчет по этой модели должен начинаться с определения вероятности перехода и концентрации компонента, участвующего на данной фазе перехода, в первом подслое. На первой фазе вероятность пе­рехода компонента 1 из первого подслоя во второй можно определить по зависимости (4.65), принимая У = 1. Концентрация первого компонента в первом подслое после этой фазы перехода может быть опре­делена следующим образом:

лз-і) y(l) _ ^->(і, лз-і) р (і,2,ш)

(Ж)

В данном случае более удаленный от центра циркуляции подслой отсутствует, следовательно, из этого подслоя на данной фазе перехода компонент 1 не переносится.

Зависимость (4.66) используется для всех подслоев, кроме последнего, так как для каждого после­дующего известна величина РгJ-~l,1,т^ V"k]. Например, при расчете концентрации во втором под­

слое эта величина будет равняться объему первого компонента, перешедшего из первого подслоя во второй на этой фазе перехода, т. е. ^ 3(12 Ж фк)

При расчете концентрации первого компонента в последнем подслое можно использовать следую­щую зависимость:

В соответствии с этой формулой в подслой п будет поступать количество ключевого компонента 1, пропорциональное не объему последнего подслоя на данной фазе перехода, а объему.

В процессе работы барабанного смесителя непрерывного действия в него поступают те или иные компоненты. Они могут поступать в смеситель как в непосредственной близости от загрузочного края барабана, так в любом другом сечении по его длине.

Их попадание в барабан полностью меняет как конфигурацию слоя, так и разбивку слоя в попереч­ном сечении по подслоям. Может измениться также концентрация смешиваемых компонентов в под­слоях, поэтому необходимо использовать механизм пересчета концентраций компонентов по подслоям, изложенный в [36].

Достоинством изложенного выше подхода к моделированию процесса смешивания в барабанном смесителе непрерывного действия является сохранение порядка разбиения на подслои циркуляционного контура в любом поперечном сечении, т. е. толщина подслоя рассчитывается по одной и той же зависи­мости (4.21). Коэффициент вероятности перехода частиц ключевого компонента РО, 7 определяется экс­
периментально по тем же методикам, что и для смесителей периодического действия. С учетом того, что порядок разбиения на подслои сохраняется, можно использовать одно значение ЯО^ j при моделиро­вании процесса смешивания по всей длине барабана.

Также имеется возможность сопоставимой оценки качества смеси в любом сечении смесителя, на­пример С использованием коэффициентов неоднородности V$, ESS.

На основе предложенной модели процесса приготовления многокомпонентных смесей разработана программа расчета на ЭВМ основных режимных и геометрических параметров барабанного смесителя непрерывного действия.

В заключение следует отметить, что предложенная математическая модель может быть использо­вана при описании процесса непрерывного смешивания в циркуляционных смесителях других типов, поскольку в ней учитываются только общие закономерности движения компонентов как в продольном, так и в поперечном сечениях смесителя. Она может быть использована и для описания других процес­сов, в частности процесса сушки во вращающемся барабане [37 - 40].