ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

ПДЕПТПФПКАЦИЯ ПАРАМЕТРОВ П ПРОВЕРКА АДЕКВАТПОСТП МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРОЦЕССА СМЕШПВАПИЯ

Проведение третьего заключительного этапа системного анализа - идентификации неизвестных па­раметров математических моделей процесса смешивания и проверки их адекватности по эксперимен­тальным данным - покажем на примере послойной модели.

Идентификация параметров математической модели сводится к определению по эксперименталь­ным данным наилучшей оценки константы POjj.

Для идентификации параметра POij и проверки адекватности математической модели эксперименту было проведено несколько серий параллельных опытов по сегрегации бинарных композиций модель­ных смесей в барабанном смесителе диаметром 0,25 м и длиной 0,08 м. В качестве компонентов мо­дельных смесей использовались следующие сыпучие материалы: кварцевый песок, стеклянные шарики, гранулированный полиэтилен, селикагель.

Порядок проведения опытов был следующий. Готовилась двухкомпонентная смесь с определенной концентрацией ключевого компонента (за ключевой принимали компонент с меньшим диаметром час­тиц). Смесь загружалась в барабан, после чего он приводился во вращение. Через заданный промежуток времени барабан останавливался, и из объема смеси в точках, расположенных на разных расстояниях от оси вращения барабана, точечным способом отбирались пробы объемом 6 - 8 см или весом 10 - 12 г. Пробы разделяли на отдельные компоненты, которые взвешивали на весах марки ВЛК-500г-М с точно­стью до 0,01 г. По результатам взвешивания рассчитывали концентрацию ключевого компонента в каж­дой пробе. Оставшуюся в барабане смесь методом квартования делили на порции, определяли в каждой порции концентрацию ключевого компонента и затем по известной методике [7] рассчитывали диспер­сии Оуэксп. Модельные смеси приготавливались со следующими концентрациями ключевого компонен-

та: 0,466; 0,5; 0,666. Объемная загрузка смесителя изменялась от 700 до 900 см, а угловая скорость вращения барабана - от 1,56 до 4 с-1.

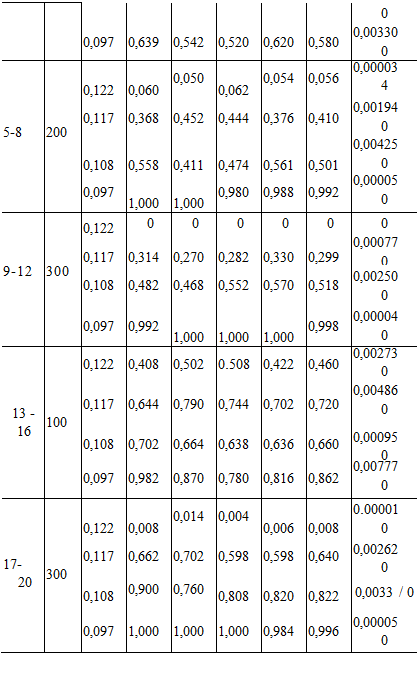
Экспериментальные данные обрабатывались по общепринятым методикам [4, 41, 42]. Прежде всего проводилась проверка результатов параллельных опытов на однородность по критерию Кохрена. В ка­честве примера проведена проверка для смеси, состоящей из кварцевого песка (средний диаметр частиц 0,2 мм) и стеклянных шариков (средний диаметр 0,8 мм), с концентрацией ключевого компонента 0,466 и 0,666. В данном случае объемная загрузка была равна 900 см3. Угловая скорость вращения барабана - 1,56 с"1. Текущие значения концентрации определялись через промежутки времени 100, 200 и 300 с от начала вращения барабана. Результаты опытов представлены в табл. 4.1.

4.1. Результаты исследования процесса смешивапия песка и стекляппых шариков

Для каждой серии параллельных опытов вычисляли среднее арифметическое значение концентрации Cj, дисперсии S] и далее проводили проверку воспроизводимости опытов по критерию Кохрена Gv. Ес­ли 6j, < (7|абл для уровня значимости Р = 0,05, то опыты считаются воспроизводимыми, а оценки дис­персии - однородными. Для рассмотренного случая Gv = 0,195, а 6гТабл = 0,221.

Аналогичная проверка на однородность дисперсии проводилась и для других серий опытов. Экспе­риментальные значения Cj использовались для нахождения параметров Яф 2- По методике, аналогич­ной приведенной в работе [4], для всех серий опытов, в которых смесь приготавливалась из одинаковых компонентов, находили оптимальные значения ЛЭц 2- В частности, для рассмотренной смеси из песка и стеклянных шариков 2 = 0,128.

По результатам анализа проб, полученных методом квартования для каждого опыта определяли дис­персии концентрации о2эксп [4]. Поскольку выборочную дисперсию можно рассматривать как параметр, ха­рактеризующий качество смеси, для экспериментальных данных, полученных при одинаковых исходных концентрациях и угловых скоростях вращения барабанов, приводилась проверка опытов на воспроизводи­мость по критерию Кохрена с использованием следующей формулы:

4 (

I 2 _ -=2

УУэксп ^эксп

^р=^Т7--------------------- -• (4.69)

3YY _2 _-=2 I2

J / у / у у4 уУэксп ^Уэксп/

7=1 Ь1

Как видно из табл. 4.1, все опыты воспроизводимы.

Проверка адекватности математической модели при найденном параметре ЛЭц 2 эксперименталь­ным данным о2эксп (стб. 9 табл. 4.2) проводилась следующим образом. С использованием математиче­ской модели рассчитывались значения о2 (стб. 10 табл. 4.2). Вычислялась остаточная дисперсия 52ст, дисперсия воспроизводимости 52осп, дисперсия среднего значения S2 и критерий Фишера Fp. Значение Fp сравнивали с табличным значением FTабл [25], найденным при соответствующих степенях свободы f = 5-1=4и^ = 4-1=Зи уровне значимости Р= 0,05. Для рассматриваемых примеров FTабл = 9,12. Ре­зультаты вычислений представлены в табл. 4.2. При Fp < FTабл математическая модель адекватна реаль­ному процессу. Как видно из табл. 4.2, для всех случаев математическая модель адекватна эксперимен­ту.

Послойная модель является частным случаем ячеечной модели, рассмотренной выше, когда можно считать, что исходные концентрации в элементарных объемах в пределах одного слоя одинаковы. Если в барабанный смеситель компоненты загружать последовательно при вращающемся барабане [43], то результаты расчетов текущего качества смеси, например коэффициента неоднородности V, выполнен­ные по послойной и ячеечной моделям, будут практически полностью совпадать. Незначительные от­клонения возможны лишь в пределах одного перехода. Учитывая, что разница времени одного перехо­да в указанных моделях незначительна (в проведенных опытах для послойной модели времени одного перехода 0,25 с, а в ячеечной - порядка 0,05 с) и абсолютные значения этих времен меньше времени процесса, при проведении практических расчетов удобнее пользоваться более простой послойной мо­делью.

При идентификации параметров ячеечной модели можно использовать способ исследования процесса смешивания сыпучего материала [43], сущность которого заключается в том, что ключевой компонент вносят в слой материала, неподвижного относительно вращающегося барабана.

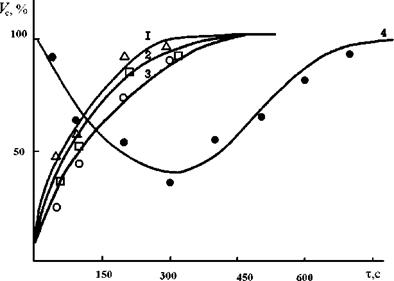
На рис. 4.11 показаны графики изменения коэффициента неоднородности Vc во времени. Компо­ненты смеси - песок и стеклянные шарики. Концентрация песка - 0,466, Кривые 1, 2, 3 построены для случая сегрегации однородной исходной смеси при угловых скоростях вращения барабана 2,07; 2,89; 3,6 с-1, кривая 4- для случая, когда сначала в смеситель загружали основной компонент (стеклянные шарики), а затем при вращающемся барабане равномерно по его длине загружали ключевой компонент. Сравнивая численные значения коэффициентов неоднородности при одинаковых значениях х, можно сделать вывод о том, что коэффициент неоднородности нелинейно зависит от угловой скорости враще­ния барабана.

Из характера кривой 4 видно, что коэффициент неоднородности сначала уменьшается, а затем на­чинает возрастать. Это можно объяснить тем, что сначала часть ключевого компонента из наружных подслоев (в рассматриваемом примере это 10 подслоев при общем количестве 38), где первоначальная его концентрация была равна единице, переходит в подслои, находящиеся ближе к центру циркуляции, в результате чего распределение ключевого компонента становится более равномерным. Таким обра­зом, концентрация компонента в наружных подслоях постоянно уменьшается, а во внутренних - увели­чивается.

Значение концентрации в наружном слое достигает средней величины раньше, чем этой величины дос­тигают концентрации подслоев, находящихся в непосредственной близости к центру циркуляции. В дальнейшем концентрация во внешних подслоях становится меньше средней, качество смеси ухудша­ется и коэффициент неоднородности, естественно, увеличивается.

Проведенные экспериментальные исследования по смешиванию частиц разного цвета и диаметров наглядно показали, что при большом различии в размерах мелкие частицы движутся к центру циркуля­ции достаточно плотным фронтом, т. е. всегда можно выделить несколько подслоев с повышенной кон­центрацией мелкой фракции, которые постепенно перемещаются к центру циркуляции и в конечном счете образуют вокруг этого центра ядро сегрегации. Из этого следует сделать вывод о том, что при ор­ганизации процесса смешивания компонентов, склонных к сегрегации в циркуляционных смесителях, можно и нужно управлять интенсивностью и эффективностью процесса за счет изменения регламента загрузки компонентов. Особенно это важно при приготовлении многокомпонентных смесей.