ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

ОПРЕДЕЛЕППЕ ГРАППЦ ВЕЕРА ЧАСТПЦ, ПАДАЮЩИХ С ЛОПАСТЕЙ

В большинстве случаев при расчете процесса, реализуемого в барабане с внутренними устройства­ми, необходимо знать параметры движения не только отдельной частицы, но и всей совокупности час­тиц, падающих с лопастей. Так, например, при расчете барабанных сушилок необходимо знать количе­ство частиц, находящихся в состоянии падения с лопастей, время их падения и степень разрыхления, т. е. расстояния между отдельными частицами [12]. Параметры веера частиц сыпучего материала при падении их с лопастей необходимо знать и при описании процесса дозирования барабанным питателем [13].

Рассмотрим образование веера сыпучим материалом, ссыпающимся с лопасти вращающегося бара­бана. В работе [14] показано, что при ссыпании материала с лопасти наиболее удаленные на момент на­чала движения от ссыпающего края лопасти частицы движутся в потоке материала на лопасти по более близким к свободной поверхности слоям потока и имеют в момент отрыва от лопасти большие скоро­сти. Границы веера падающего материала образуют частицы с hj = 0 и hj= Дпах, где hj - расстояние ме­жду частицей и ссыпающим краем лопасти в момент отрыва частицы от лопасти в направлении, нор­мальном к вектору скорости частицы. Таким образом, границы веера падающего с лопасти материала образуют частицы, которые на момент начала движения на лопасти находятся на максимальном и ми­нимальном удалении от ссыпающего края. Частицы с Д11ах > Д > 0 во время падения находятся внутри веера материала, а положение их в веере определяется, как следует из сказанного выше, расстоянием частиц до ссыпающего края на момент начала движения их на лопасти.

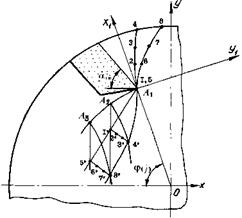
На рис. 3.3 изображена окружность, образуемая ссыпающим краем лопасти при вращении барабана. Точки А]_, /Ь, Аз, Аз на окружности - положения ссыпающего края лопасти в различные моменты време­ни t, причем tA-tA= tA - tAi=tAi-tA4=At.

Параболы, проходящие через точки Aj, есть траектории движения частиц, оторвавшихся от лопасти в соответствующие моменты времени с максимальными начальными скоростями из всей совокупности частиц, оторвавшихся от лопасти в момент Д т. е. эти частицы на момент начала движения на лопасти были удалены от ссыпающего края на максимальное расстояние.

Точки Д - положения этих частиц в момент времени t j. Точки А, Д, Д, Д образуют верхнюю границу веера, которая может быть получена при соединении этих точек плавной кривой. Очевидно, что точность такого определения границы веера определяется величиной At. В неподвижной декарто­вой системе координат положение точек Д определится координатами х и у. Тогда линия границы вее­ра будет параметрически определена.

Подобным образом определяется нижняя граница веера, образуемая частицами, оторвавшимися в момент времени tj с минимальными начальными скоростями.

Рис. 3.3. Схема траектории падения отдельных частиц

Изложенный на примере определения границ веера падающего с лопасти материала подход приме­ним для более детального изучения веера, например для определения коэффициента разрыхления мате­риала в веере, площади поперечного сечения веера и т. д.

Рассмотрим положение ссыпающегося края, характеризуемого углом ср(/) (рис. 3.4). Частица нахо­дится в данный момент на ссыпающем краю, начало движения на лопасти при угле ф( /) - то, где т - время движения частицы по лопасти; ю - угловая скорость вращения барабана; (Хм, - угол трения покоя.

Будем считать, что движение частицы на лопасти осуществляется по закону движения тела на на­клонной плоскости, т. е. это движение равноускоренное с ускорением а [14]: а= f[fu, где 4 fn -

коэффициенты трения покоя и движения.

получим в результате решения уравнения время, которое затратит частица, самая удаленная от ссы­пающего края, на движение по лопасти.

По найденному времени рассчитывается угол тю и определяется положение частицы на лопасти в системе координат, жестко связанной с лопастью, например в системе XS Y (рис. 3.4).

Так определяются координаты частицы на лопасти, которая в положении лопасти ф(/) будет нахо­диться на ссыпающем краю и при падении вместе с другими частицами образует верхнюю границу вее­ра. Подобным образом можно определить положения всех частиц на лопасти, которые в положении ло­
пасти ф(/) будут находиться на ссыпающем краю, но ввиду трудоемкости такой работы следует ограни­читься небольшим их количеством.

На рис. 3.5 изображена часть окружности, образованной ссыпающим краем лопасти при вращении барабана. Координаты XOY жестко связаны с лопастью, они неподвижны, их начало - в центре бара­бана. Точки А, Az, A3 - положения ссыпаюшего края в моменты времени ґаі, (42, (аз - Точки 1 - 8 - по­ложение частиц материала на лопасти на начало их движения по ней, точки V - 8' — положение этих частиц в момент времени £41- Частицы 1-4 находятся на ссыпающем краю в момент tja, точки 5 — 8 —

МОМеНТ £43.

Частицы, оторвавшиеся от лопасти в моменты tja, (аз, движутся по параболическим траекториям. Ограничившись количеством рассматриваемых одновременно оторвавшихся частиц равным, например, 4, расположив частицы на лопасти насколько возможно равномерно, определив их координаты на лопа­сти, рассчитав время их движения на лопасти, начальные скорости при отрыве от лопасти с учетом ок­ружной

3.1. ЭКСПЕРПМЕПТАЛЫЮЕ ПССЛЕДОВАППЕ ДВПЖЕППЯ ЧАСТПЦ В БАРАБАПЕ С