ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

МОДЕЛИРОВАНИЕ ПРОЦЕССА ГРАНУЛИРОВАНИЯ

Поскольку в барабанных грануляторах рост гранул осуществляется либо за счёт наслоения плёнки при окатывании, либо за счёт диспергирования жидкости на поверхность частиц, находящихся в со­стоянии падения с лопасти, рассмотрим моделирование процесса гранулирования в окаточных бараба­нах и в грануляторах-сушилках.

5.2.1. ГРАНУЛИРОВАНИЕ МЕТОДОМ ОКАТЫВАНИЯ

Метод гранулирования скатыванием, при котором формирование гранул достигается агломерацией или наслоением, широко используется в различных отраслях народного хозяйства, и особенно в хими­ческой промышленности при крупнотоннажном производстве минеральных удобрений [1].

Одним из основных показателей эффективности работы гранулятора является выход товарной фракции, т. е. процентное содержание в готовом продукте гранул определенных размеров [5]. При ис­пользовании барабанов для дражирования сыпучих материалов [9, 10] необходимо нанести на частицы пленку одинаковой толщины, т. е. в конечном счёте желательно получить монодисперсный готовый продукт. Таким образом, при проектировании новых и модернизации действующих барабанных грану­ляторов необходимо иметь возможность не только прогнозировать гранулометрический состав готово­го продукта, но и рассчитывать оптимальные геометрические и режимные параметры гранулятора.

Для решения этой задачи широко используют математическое моделирование процесса гранулиро­вания. Наиболее полный и критический анализ известных моделей приводится в работах [1, 3]. При разработке многообразных моделей не было уделено достаточного внимания на качественный анализ рассматриваемого процесса с целью выявления наиболее общих закономерностей движения сыпучих материалов, определяющих кинетику гранулообразования.

Непрерывный процесс гранулообразования следует рассматривать как сложную физико­механическую систему (ФМС) [11]. Будем рассматривать второй уровень иерархии, т. е. учитывать за­кономерности, присущие макрообъёмам рабочего пространства, и воспользуемся математическим ап­паратом марковских цепей. Предположим, что гранулирование осуществляется в результате двух по­следовательно реализующихся процессов: сегрегации частиц по размерам в поперечном сечении вра­щающегося барабана и роста гранул за счёт наслоения на них плёнки. Разделим барабан по длине на участки и будем считать, что в пределах участка состояние системы и, прежде всего, её гранулометри­ческий состав не изменяются во времени. Принимаем, что состояние системы, т. е. переход частиц из одного участка в другой, происходит скачкообразно. При этом за один переход совершаются два про­цесса: сегрегация гранул по размерам и их рост. Пусть в любом поперечном сечении барабана имеется достаточное количество частиц к-й фракции и они равномерно распределены в пределах каждого под­слоя, т. е. гранулометрический состав есть функция только радиуса движения частиц в поднимающемся слое. В соответствии с принятым допущением разделим весь материал на поднимающиеся слои, как это показано на рис. 2.2.

Параметры, характеризующие распределение и движение сыпучего материала в поперечном сече­нии вращающегося барабана, можно определить, используя зависимости (2.2) - (2.32).

Поскольку гранулометрическая характеристика материала определяется сиговым анализом и пред­ставляется дискретными функциями [1], будем считать, что на входе в рассматриваемый участок барабана j весь материал состоит из т фракций и известны концентрации этих фракций по подслоям, т. е. известны величины LJ і, где к - номер фракции, к= 1, 2, ..., т і - номер подслоя, і = 1, 2, ..., п j - номер участка, 7=1,2,..., А

При описании процесса сегрегации используем послойную модель процесса смешивания полидис- персного материала в поперечном сечении гладкого вращающегося барабана, которая рассмотрена в разд.

4.2.1.

Согласно данной модели концентрацию ключевого компонента (частиц определенной фракции) после процесса сегрегации на участке jможно определить, используя зависимости (2.25) - (2.27): для первого подслоя

ДЛЯ 17-ТО ПОДСЛОЯ

(5.4)

для остальных подслоев

Ски = (v>ck,,j-1 - CKiJVB + Pk^jjVn)jс, (5.5)

где Vi - объём /-го подслоя на участке у; Рк, і у + j - вероятность перехода частицы из подслоя і в под­слой / + 1; Pk, і. ij - вероятность перехода частицы из подслоя У - 1 в подслой /

Пользуясь зависимостями (5.3) - (5.5), последовательно изменяя і от 1 до щ можно рассчитать кон­центрации всех фракций во всех подслоях. Следует отметить, что вероятности переходов частиц из слоя в слой для разных фракций различны. Численные значения вероятностей Рк, /+ і,/ определяются по формулам, аналогичным (2.20) - (2.21):

к m

Рк, 1,1+1,j = ^ДД - Czl+l j_l)-'*2^PlCl l+l j_l, (5-6)

z= £=к

где Pz — вероятность перехода частиц фракции z из подслоя і в подслой і + 1 при нулевых концентрациях в нём частиц фракции z и более мелких фракций; {Pz - Р,) - вероятность перехода частиц фракции z из подслоя і в подслой і + 1 при единичной концентрации в нём частиц фракции £.

Значения Pz и Pt находятся при идентификации параметров математической модели эксперименту по методике, изложенной в разд. 4.3. Учитывая, что точность расчётов по предлагаемой методике зависит от числа фракций, на которые делится материал, находящийся в барабане при большом количестве фракций, при использовании зависимости (5.6) необходимо проводить значительные экспериментальные исследо­вания. Для практических расчётов можно предложить следующую формулу:

где Рк — вероятность перехода частиц фракции к из подслоя і в подслой /+ 1 при единичной концентра­ции в нём частиц самой крупной фракции; d1+l - средний диаметр частиц в подслое і + 1.

Зависимость (5.7) справедлива при dk<d, при dk > У Д /+ к 7 = 0. Данная зависимость получена пу­тём выражения концентрации ключевого компонента через величины Д, d, dm в формуле

Р=Р0и(1-С), (5.8)

которая используется при расчёте двухкомпонентной смеси. В данном случае полидисперсный матери­ал заменяется бинарной смесью, состоящей из частиц с диаметром dk и d. Зависимость (5.8) в разд. 4.3 проверена экспериментально.

Рассмотрим вторую стадию процесса - рост гранул. Для математического описания воспользуемся механизмом роста гранул за счёт наслоения плёнки [1], поскольку он позволяет учитывать истирание гранул при их движении в барабане. Сделав соответствующие допущения [1], запишем:

dkiddki = [2tCg/n),kgdz,

где did ~ диаметр частиц фракции к, і - длина пути, проходимого гранулами подслоя в скатывающемся слое в единицу времени; - толщина плёнки, которая наслаивается на гранулу за один её оборот во­круг собственной оси, для 1-го подслоя участка у.

Уравнение (5.9) представляет собой математическую модель роста частицы при гранулировании методом скатывания. В отличие от модели [1], в предлагаемой введена длина пути гранул в скатываю­щемся слое с учётом номера подслоя. Это обусловлено тем, что в зависимости от радиуса движения в поднимающемся слое, т. е. от номера подслоя, за один оборот вокруг центра циркуляции гранулы про­ходят разный путь (см. рис. 2.2). Гранулы, находящиеся в подслое с большим номером, т. е. движущиеся по меньшему радиусу R,■, в скатывающемся слое проходят меньший путь, но и время одного оборота вокруг центра циркуляции у них меньше, т. е. они чаще появляются в скатывающемся слое. Именно по­этому в уравнение (5.9) введена длина пути гранул за единицу времени. Экспериментальные исследо­вания, проведённые путём наблюдения за движением меченой гранулы в поперечном сечении вра­щающегося барабана, показывают, что численные значения і а для разных подслоев могут отличаться более чем на 20 %,

В модели также введена зависимая от номера подслоя и участка толщина пленки Х1}. Ранее [1] учи­тывалось изменение данного параметра только по длине барабана. Использование переменной по под­слоям Ху обусловлено следующими основными причинами: при подаче связующего на открытую по­верхность скатывающегося слоя [ 1 ] неодинакова вероятность попадания его на частицы, находящиеся в разных подслоях; скорость движения частиц в скатывающемся слое нелинейно зависит от радиуса их движения в поднимающемся слое, и, следовательно, градиент скорости по подслоям непостоянен, а именно от абсолютной скорости частиц и разницы скоростей в соседних (контактирующих между со­бой) скатывающихся подслоях во многом зависит интенсивность истирания гранул и как следствие Х1}.

Определим значение і Cl, для чего расположим систему координат Х CY, как показано на рис. 2.2. Верхний участок границы раздела слоев можно считать прямой, совпадающей с осью СХ, а нижний - удовлетворительно описывается зависимостью (2.32). Учитывая это, можно записать:

Х1В і

l'c,= j ЛІ^ + ІУ)2 dx+^в}-В2 cos81 , (5.10)

о

где t а - длина пути грапулы /-го подслоя в скатывающемся слое; ХВі~ координата точки перехода /- й час­тицы из скатывающегося слоя в поднимающийся [см. уравнение (2.32)]. После интегрирования (5.10) полу­чим:

и, подставив значение Хіві, найдём численное значение t сі - Время одного оборота частицы /-го подслоя вокруг центра циркуляции где Vjj - объём /-го подслоя на участке у; Rcj - расстояние от оси вращения барабана до центра циркуля­ции (2.19).

С учётом (5.11), (5.12) запишем:

^/ = С-ДЦ/- (5ЛЗ)

Рассмотрим частные случаи модели (5.9) и, прежде всего, изменение параметра Ху - по толщине ска­тывающегося слоя. Возможны три типичных варианта: ку = const; уменьшается линейно по толщине

слоя, т. е. Xy = X0jR]/RCj или X}J - = X0j(RrRCj); толщина плёнки уменьшается по экспериментальному за­

антам изменения А,/по длине барабана [1]. Рассмотрим указанные варианты изменения Ху по длине ба­рабана, т. е. зависимости от времени гранулирования, и после интегрирования (5.9) получим:

В общем случае толщина истирающейся плёнки может изменяться по иным законам, чем толщина наросшей плёнки. В работе [1] приводятся результаты интегрирования уравнения (5.9) при различных законах изменения толщины истирающейся плёнки по длине барабана. Этими результатами можно воспользоваться с учётом изменения толщины нарастающей плёнки по подслоям, сделав соответст­вующие замены длины пути скатывания частиц >го подслоя.

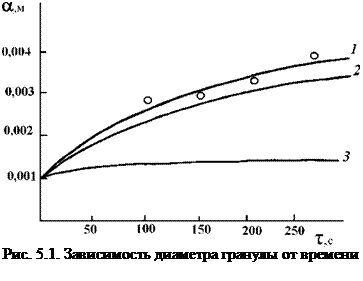
На рис. 5.1 показаны зависимости роста гранул от времени гранулирования при разных законах из­менения величины X0j по толщине скатывающегося слоя для частиц ретура, движущихся по открытой

поверхности (кривая 1) и в непосредственной близости к центру циркуляции (кривые 2 и 3). Если Ху

постоянна по толщине скатывающегося слоя, то размер гранул определяется только суммарной длиной пути в скатывающемся слое и, как видно из сравнения кривых 1 и Д несущественно зависит от положе­ния частиц в слое. При Xy = XQjRijRCj конечный размер гранул отличается более чем в два раза (кривые 1

и 3).

5.2.2. ГРАНУЛИРОВАНИЕ В БАРАБАННОМ ГРАНУЛЯТОРЕ-СУШИЛКЕ

Математическая модель процесса гранулирования в аппарате БГС, учитывающая влияние расхода и распределения частиц ретура по размерам, а также продольное перемешивание твёрдой фазы на кине­тику роста и гранулометрический состав продукта, приводится в работе [12]. В модели сделаны сле­дующие допущения: расход гранул по аппарату постоянен, форма гранул сферическая, агломерация и истирание гранул отсутствуют. Первое допущение означает, что зарождение новых центров гранулооб- разования не учитывается. Допущение выполняется при небольшом количестве расходуемой пульпы.

Последнее допущение, очевидно, выполняется в стационарном режиме работы при достаточно боль­шой разнице между размерами частиц товарной фракции и новых центров гранулообразования, что на­блюдается в реальных процессах.

При сделанных допущениях составлен материальный баланс процесса гранулирования в БГС. В ка­честве основного уравнения гранулирования принят аналог уравнения массопередачи по газовой фазе:

- = К{С-СЛ = КСа, (5.17)

Fdi р v '

где С= G. K Ар, /(Zр) - относительная доля твёрдой фазы во внешней газовой среде, м3 тв. фазы/м3 газа; Ср - относительная объёмная доля нанесенного вещества твердой фазы во внешней газовой среде, образую­щаяся за счёт высыхания микрокапель и истирания гранул, м3 тв. фазы/м3 газа; К - коэффициент массо - передачи для единичной гранулы, кг/(м с).

В работе [12] получены формулы для определения диаметра гранул в зависимости от времени пре­бывания их в аппарате, в том числе и для случая полидисперсного ретура. Основные допущения работы [12] подтверждены экспериментально [13, 14]. Для этого гранулометрический состав готового продукта рассчитывался на ЭВМ и сравнивался с экспериментальными данными. Результаты сравнения показа­ли, что данная математическая модель может быть использована при расчёте БГС, если имеются опыт­ные данные о длине зоны факел-завесы и распределении гранул по времени пребывания в аппарате.