ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

МАТЕМАТИЧЕСКОЕ ОППСАППЕ ПРОЦЕССА ДВПЖЕПИЯ СЫПУЧЕГО МАТЕРИАЛА

2.3.1. ДВИЖЕНИЕ В ПОПЕРЕЧНОМ СЕЧЕНИИ БАРАБАНА

Как уже отмечалось ранее, переход сыпучего материала от покоя к движению определяется равно­весием отдельных частиц. При вращающемся барабане на частицу, находящуюся на открытой поверх­ности сегмента материала, будут действовать гравитационные и центробежные силы (см. рис. 2.4, в). Составим уравнение равновесия частицы:

Численное значение угла аш, при котором частица начинает двигаться, зависит от ее положения на открытой поверхности, т. е. от величины угла ф. В наиболее неблагоприятных условиях с точки зрения перехода от покоя к движению находится частица, расположенная в точке А, т. е. при ф = 8о, так как на нее действует максимальная тормозящая составляющая от центробежной силы. Переход в движение именно этой частицы характеризует устойчивое движение всех частиц, находящихся на открытой по­верхности сегмента материала. Из уравнения (2.1) угол осш, при котором начинается это движение, будет равен:

Таким образом, положение точки А можно охарактеризовать углом 0 |, который равен сумме углов 0Сю и 80.

Рассмотрим движение сыпучего материала в поперечном сечении гладкого вращающегося цилинд­ра [9]. В системе декартовых координат XCY (см. рис. 2.2) верхний участок границы раздела слоев совпадает с осью СХ, а нижний с точностью, достаточной для практических расчетов, описывается следующим уравнением:

Уі=аХЇ,

27?sm80 sin(50 -52)

1 ДС а — r по*

[27?sin 50 sin(50 - б,) - 7?sin 8, ]

Определим площадь поперечного сечения (5^) материала, неподвижного относительно обечайки, и координаты его центра тяжести ( , ^ ) [10]. Площадь S„ есть сумма двух площадей: площади кругово­

го сегмента Sad и фигуры, ограниченной прямой CD, дугой окружности BD и кривой СВ, Scdb-

где ylB = 27?sin80 sin(80 -8j) - ординаты точки В в системе координат Х СУ, TjXjj) =-у/тг2 ~(уг - RcosS^2 ґ2(Уі) = л[ЇФ ■

После подстановок, интегрирования и несложных преобразований выражение (2.5) принимает вид:

Координаты центра тяжести найдем по следующим формулам:

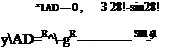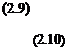Координаты центра тяжести кругового сегмента равны:

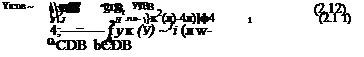Координаты определим по следующим формулам:

После подстановок, интегрирования и преобразований выражения (2.11, 2.12) принимают вид:

1 f ^ sin3 8j k-lj^-TfcosSj)2]^3

y. CDB~~ ' l"

+7?cos5j

Подставив (2.9 - 2.14) в формулы (2.7, 2.8), нетрудно определить значения У, У - В системе координат ХОУ (см. рис. 2.2) координаты центра тяжести материала, неподвижного от­носительно обечайки, будут равны:

У = У cos(ara -50 - Ф)- (У ~ T^cosSj)- sin(ara + 50 - 82); (2.15) у+ = У sin(ara + 50 - §0 + (л+ ~~ 7?cos §!) • cos(ara + 50 - 82). (2.16)

Потенциальная энергия, которой обладает материал поднимающегося слоя, будет равна:

где L - длина барабана; р - насыпная плотность материала.

Реальный минимум потенциальной энергии для данной системы

Подставив в уравнение (2.17) значения S„ из формул (2.4),(2.5) и у из (2.16) и приравняв Пп к Ппип (2.18), получим уравнение с одним неизвестным 8ц Данное уравнение трансцендентно относительно 8ц поэтому значение 8і находится численным методом. Отметим, что 8і є [8ц 0].

При известном значении 8і координаты центра циркуляции ac, Rc и толщину скатывающегося слоя CNможно определить по следующим формулам:

«С = «ш + Ф-Ф; Rc = RcosS1; (2.19)

CN= Rcos 8, - R——. (2.20)

1 cos(80 — ) v y

Координаты точек 4и5в системе координат ХОУ определим по зависимостям

^=7?sin(ara + 50); yA= -7?cos(ara - 80); хв= -7?sin(50 - ara); yB= -7?cos(50 - aj. (2.21)

Для машин барабанного типа периодического действия коэффициент заполнения барабана мате­риалом постоянен по его длине, поэтому массу материала, находящегося в барабане, можно найти так:

Л/Г 0,5Zp7?2

мп = —L--------------------------------- .

250 - sin250

Масса материала поднимающегося слоя будет равна:

Mn = LpSn,

где S, і - сумма площадей Sad и Scdb, определенных по формулам (2.4) и (2.6).

Массу материала, находящегося в скатывающемся слое, можно определить как разность Мо и Мп (2.22, 2.23). Отметим, что при таком подходе не делается никаких допущений о степени разрыхления материала скатывающегося слоя, а тот факт, что материал поднимающегося слоя имеет определенную постоянную удельную плотность р, не вызывает сомнений.

Зависимости (2.1) - (2.23) позволяют описать распределение сыпучего материала в поперечном сече­нии гладкого вращающегося барабана.

Экспериментальные данные [11] позволяют сделать вывод о том, что движение частиц, находящих­ся в скатывающемся слое, можно считать равноускоренным на участке разгона (выше сечения CN, рис. 2.2) и равнозамедленным на участке торможения (ниже сечения CN).

Как показывают результаты фото - и киносъемки, скатывающийся слой материала состоит из ряда подслоев. При допущении, что толщина каждого подслоя равна диаметру частиц и что взаимодействия между отдельными частицами, в том числе и соударения, учитываются коэффициентами трения fg уравнение для определения скорости их движения, полученное с использованием методов механики многофазных концентрированных дисперсных систем [12], упрощается до уравнения, получаемого при одночастичном подходе [13]. Учитывая это, сделаем соответствующие допущения и используем одно­частичный подход.

Уравнение движения частицы скатывающегося слоя в системе координат XAYi запишем в сле­дующем виде (см. рис. 2.2):

т+ fgmgcosac - mgsmac = 0, (2.24)

где аг - ускорение движения частицы. Из уравнения (2.24) имеем:

X = gsmac - fggcosac. (2-25)

Последовательным интегрированием уравнения (2.25) получим выражения для определения скоро­сти движения частицы и пройденного ею пути:

X = Гс =(^sinac - fggcosac)x+ Q ; (2.26)

у =0,5(^sinac - fggcosac)x2 + Qt+ C2. (2.27)

Постоянные интегрирования C и C находятся из уравнений (2.26) и (2.27) при следующих гранич­ных условиях:

ij(o) - юRc;

-4(0) *с / -‘V / 5

где Rj - радиус, на котором находится точка перехода частицы из поднимающегося слоя в скатываю­щийся.

Подставив в уравнение (2.27) значение xj, равное расстоянию до центрального сечения, можно оп­ределить время движения 7-й частицы на участке разгона:

со Д,

Совместное решение уравнений (2.26) и (2.28) дает выражение для определения скорости, которую имеет частица при прохождении центрального сечения:

(2.29)

Ординату ущ точки, через которую 7-я частица проходит центральное сечение, можно найти, ис­пользуя выражение, аналогичное полученному в работе [14]:

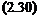cos 5,

cos(ac-ara/)

Численное значение affly находится по формуле (2.2) при подстановке вместо 8о значения 8,, а вместо R-Rj.

При принятом допущении о том, что на участке торможения частицы движутся равнозамедленно, время Хгу торможения 7-й частицы можно определить из выражения:

1 + -

где іщі - путь торможения частицы; и® - проекция скорости частицы, в момент перехода ее из скаты­вающегося слоя в поднимающийся, на границу раздела слоев.

Учитывая вывод, полученный в работе [15], о том, что длину пути частицы в скатывающемся слое можно принимать равной длине участка границы раздела слоев между точками переходов частицы из слоя в слой, значение Lu можно определить следующим образом:

Для нахождения хві необходимо совместно решить уравнение (2.3) и уравнение окружности радиу­са R;.

2atfcos5, -1 - J(2aRcos 8, -1)2 - 4а2(д2 - У? cos2 8,)

=І------------------ і?----------------- •

Значение тж = co/^cosq,, где 2, - угол между вектором окружной скорости и касательной к нижнему участку границы раздела слоев в точке перехода 7-й частицы из скатывающегося слоя в поднимающий­ся.

Время тсу пребывания 7-й частицы в скатывающемся слое определяется как сумма времени разгона тр/ и торможения Хру в поднимающемся слое будет равно х||( = 25,/со, а время цикла 7-й частицы, за которое

она совершит один оборот вокруг циркуляции - сумме времен Тсу И Т|„.

При движении в скатывающемся слое сыпучий материал разрыхляется, т. е. увеличиваются зазоры между частицами. Степень разрыхления можно характеризовать коэффициентом К. Объемный коэффи­
циент разрыхления К показывает, во сколько раз увеличивается объем, занимаемый сыпучим материа­лом в движении, по сравнению с объемом той же массы материала, находящегося в покое. Коэффици­ент разрыхления является важной характеристикой состояния сыпучего материала. В сушилках, охла­дителях, реакторах он во многом характеризует условия контакта обрабатывающего агента с обрабаты­ваемым сыпучим материалом. В смесителях от коэффициента разрыхления зависит вероятность пере­хода частиц из одного движущегося подслоя в другой.

Для выявления причины возникновения разрыхления материала при его движении в скатывающем­ся слое рассмотрим движение двух соседних частиц, вышедших из поднимающегося слоя с одного и того же радиуса последовательно одна за другой (см. рис. 2.2). Вторая частица перейдет из поднимаю­щегося слоя в скатывающийся через некоторое время T21 после перехода первой частицы. Время Т21 = dlR(j), где d— диаметр частиц. После перехода в скатывающийся слой частицы начинают двигаться рав­ноускоренно, поэтому за время х, с момента перехода второй частицы в скатывающийся слой, они пройдут разные расстояния. Расстояние между частицами к моменту времени х будет равно:

А£ = лхх12 + 0,5aXj22 -соЯсх12. (2.33)

Линейный коэффициент разрыхления Kl будет равен: KL = A£/d.

При определении коэффициента разрыхления Kl в центральном сечении в выражение (2.33) необхо­димо подставить значение х, соответствующее времени движения второй частицы до центрального сече­ния.

Следует отметить, что объемный коэффициент разрыхления К не равен линейному Кь, так как при увеличении Kl больше двух наблюдается проникновение частиц вышележащих слоев в нижележащие. Отметим также, что коэффициент Kl увеличивается с увеличением длины открытой поверхности сег­мента материала и с уменьшением угловой скорости вращения барабана.

Для нахождения среднего коэффициента разрыхления в центральном сечении скатывающегося слоя определим объем, который занимает определенное количество материала в движении:

Уд = CNvc cpLx,

где Тс. Ср - средняя скорость движения частиц в центральном сечении скатывающегося слоя.

Объем vn, который занимает такое же количество материала в поднимающемся слое, можно опре­делить, учитывая, что частицы поднимающегося слоя движутся по концентрическим окружностям с уг­ловой скоростью, равной скорости вращения барабана:

гп=0,5ю (К-Кс)1л. (2.34)

В соответствии с определением коэффициент разрыхления будет равен:

Зависимости (2.24) - (2.35) позволяют определить параметры, характеризующие движение сыпуче­го материала в поперечном сечении гладкого вращающегося барабана, необходимые для расчета машин периодического действия. Для расчета и проектирования машин и аппаратов непрерывного действия, которые все шире используются в промышленности, необходимо знать особенности движения материа­ла вдоль оси барабана.