ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

ЛОПАСТПОЙ ПАСАДКОЙ

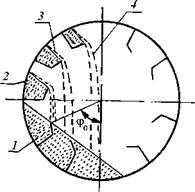
Рассмотрим распределение и движение сыпучего материала в поперечном сечении барабана с ло­пастной Г-образной насадкой (рис. 3.1). Цикл движения частицы можно разделить на четыре стадии: 1) движение в завале; 2) движение вместе с лопастью; 3) движение по лопасти; 4) свободное падение с ло­пасти.

Такая детализация процесса движения обусловлена, прежде всего, тем, что интенсивность и эффек­тивность технологических процессов, реализуемых в барабане, различны на разных стадиях движения сыпучего материала. Так, например, в работах Н. М. Михайлова [1], Л. А. Мамруковой [2], Н. А. Чемарда, Е. И. Васючкова и М. И. Бейлина [8] показано, что передача тепла на поверхность падающих частиц про­исходит на порядок эффективнее, чем на наружную поверхность слоя частиц, находящихся на лопастях и в завале, и на два порядка эффективнее, чем к частицам, находящимся внутри завала.

Рассмотрим более подробно каждую из указанных стадий движения. В зависимости от степени за­полнения барабана сыпучим материалом, формы и размера лопастей возможны два предельных случая: 1) лопасть полностью перекрывается материалом, находящимся в завале; 2) ссыпающий край лопасти на­ходится выше линии завала.

В первом случае, т. е. при большом заполнении барабана материалом, движение материала в завале можно рассматривать, не учитывая влияния лопастей. Во втором случае можно вообще не рассматри­вать завал и ограничиться только рассмотрением остальных трех стадий движения. Учитывая, что для практических расчетов в основном требуются интегральные характеристики движения сыпучего мате­риала, такие, например, как общее количество материала и время его пребывания на каждой из указан­ных стадий, нет необходимости детально рассматривать движение отдельных частиц в завале.

Рассмотрим движение частиц сыпучего материала вместе с лопастью. Зная степень занолнения бара­бана материалом, форму и размер лопастей, нетрудно определить положение лопасти (угол фо на рис. 3.1), при котором ее ссыпающий край выйдет из завала. Объем материала Vn, находящегося на лопасти, можно определить по следующей формуле:

Vn=LjdS, (3.1)

где L - длина барабана; S - область интегрирования, т. е. площадь, ограниченная лопастью, дугой обе­чайки барабана и открытой поверхностью материала, находящегося на лопасти.

Первые две границы области интегрирования нетрудно найти, поскольку они определены размера­ми барабана и лопасти, а также формой последней. Открытая поверхность материала, находящегося на лопасти в поперечном сечении барабана, образует линию, в общем случае отличную от прямой [10]. Эту линию можно определить, рассмотрев условия перехода отдельных частиц из состояния покоя в со­стояние движения относительно лопасти, используя подход, аналогичный примененному в гл. 2, при определении угла наклона к горизонту открытой поверхности сегмента материала, находящегося в ба­рабане, соответствующего началу движения отдельных частиц. Зная режимные и геометрические пара­метры барабана, а также физико-механические характеристики сыпучего материала, можно однозначно определить объем материала, находящегося на лопасти, как функцию ее положения, т. е. угла ф.

Результаты экспериментальных исследований с использованием фото - и киносъемки [5, 6] позво­ляют сделать следующие допущения при описании движения частиц сыпучего материала по лопасти: частицы ссыпаются с лопасти потоком, который состоит из ряда параллельных подслоев; в момент от­рыва от лопасти частицы, находящиеся в одном подслое, имеют одинаковые скорости. Как следствие из сделанных допущений вытекает предположение, что после отрыва от лопасти частицы не соударяются друг с другом, поэтому при описании движения сыпучего материала в поперечном сечении барабана с лопастной насадкой может быть использован одночастичный подход.

Обычно барабаны с лопастной насадкой имеют малые угловые скорости вращения, и поэтому угол наклона к горизонту границы раздела движущегося и неподвижного относительно лопасти материала практически не зависит от положения лопасти. Исходя из этого, можно считать, что на частицу, движу­
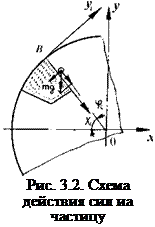
щуюся относительно лопасти, действует только сила гравитации, в то время как на частицу, неподвиж­ную относительно лопасти, действует еще и центробежная сила. Уравнение равновесия движущейся частицы в подвижной системе координат XBY (рис. 3.2) можно записать в виде:

т+ fRmgco$a-mgsma = 0 , (3.2)

где х= а - ускорение движения частицы.

Система координат располагается таким образом, чтобы ось совпадала с подслоем, в котором дви­жется частица, а начало координат - с точкой перехода рассматриваемой частицы из неподвижного слоя в движущийся.

Из уравнения (3.2) найдем ускорение, с которым движется частица

х= а = ,gsin а - T^cos а.

Последовательным интегрированием (3.3) получим зависимости для определения скорости движения частицы и пройденного ею пути [5]:

Х[ = vCK = g(sm а — fa cos а) т + Сх; (3.4)

хх = 1 = 0,5^(зіпа - fR cosa)x2 + C{i+ C2. (3-5)

Постоянные интегрирования C и Сг находим из уравнений (3.4) и (3.5) при следующих граничных условиях:

xY (0) = со Rj cos((p; - a);

*i(0) = 0,

где R - расстояние от оси вращения барабана до начала координат; фу - угол, характеризующий поло­жение точки перехода частицы из неподвижного слоя в движущийся (см. рис. 3.2); a - угол наклона плоскости, по которой движется частица.

При движении относительно лопасти сыпучий материал разрыхляется. Природа разрыхления ана­логична, описанной в гл. 2 для материала скатывающегося слоя. Для количественной оценки разрыхле­ния можно использовать формулы вида (2.33)-(2.35).

Движение частицы в сечении барабана после отрыва ее от лопасти можно рассматривать как свобод­ное падение тела в гравитационном поле с некоторой начальной скоростью. Уравнение траектории дви­жения 7-й частицы в системе координат ХОУможно записать так (см. рис. 3.2):

х= cos фл н———і - х vqj ■ cos a ; (3.6)

sin a

где hj - расстояние между частицей и ссыпающим краем лопасти в момент отрыва частицы от лопасти в направлении, нормальном к вектору скорости частицы; т - текущее время с момента отрыва частицы от лопасти.

Время падения частиц с лопасти хп определяется с момента отрыва их от лопасти до момента со­прикосновения с открытой поверхностью завала. Для определения численного значения хп необходимо решить совместно уравнения (3.6), (3.7) и уравнение открытой поверхности завала.

Перемещение частицы вдоль оси барабана будет складываться из ее перемещения при движении по лопасти, в падении и при движении по открытой поверхности завала [9]. Во время падения с лопасти поток частиц сыпучего материала разрыхляется. Степень разрыхления потока численно можно харак­теризовать коэффициентом разрыхления. По аналогии с коэффициентом разрыхления в скатывающем­ся слое К - коэффициент разрыхления потока частиц, ссыпающихся с лопасти, можно представить в виде отношения объема Vg, который занимает сыпучий материал массой Мв падении, к объему У„ , за­нимаемому таким же количеством материала в покое, т. е. на лопасти.