ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА
ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОНИСАНИЯ ДВИЖЕНИЯ СЫНУЧЕГО МАТЕРИАЛА
В настоящее время при описании движения сыпучего материала во вращающемся барабане используется либо "одночастичный" подход [7], при котором рассматривается равновесие отдельной частицы, либо метод "вязких течений" [2], согласно которому движение сыпучего материала рассматривается как течение вязкопластичной среды.
Первый подход успешно можно использовать только при описании свободного движения, например при ссыпании материала с лопастей, а основной недостаток второго подхода заключается в том, что зависимости, которые в нем используются, содержат эмпирические коэффициенты, требующие определения на лабораторных установках. Кроме этого, метод "вязких течений" описывает симметричную относительно центра циркуляции границу раздела слоев, что не соответствует реальной картине, особенно при скоростях вращения барабана больших 0,2 от критической.
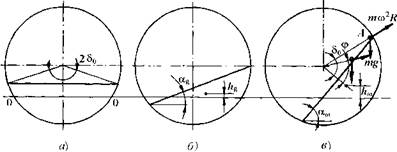
Поместим некоторое количество материала в горизонтальный барабан и рассмотрим его поперечное сечение (рис. 2.4, а). Горизонтальную линию, проведенную через центр тяжести сегмента материала, открытая поверхность которого горизонтальна, примем за "нулевой уровень" (линия 0-0, рис. 2.4, а). Данное положение системы соответствует теоретическому минимуму потенциальной энергии. Здесь и в дальнейшем под системой будем понимать совокупность частиц, неподвижных относительно обечайки барабана. Система самостоятельно не может занять указанное положение, поскольку существует трение между отдельными частицами, а также между частицами и обечайкой, Если барабан привести во вращение, а затем остановить, то открытая поверхность материала будет наклонена к горизонту под углом трения движения со, (рис. 2.4, б). Данное положение соответствует реальному минимуму потенциальной энергии, который система может достигать самостоятельно.
Если барабан снова привести во вращение, то некоторое время все частицы будут неподвижны относительно обечайки барабана, т. е. будут вращаться вместе с ней. Движение частиц по открытой поверхности сегмента начнется в тот момент, когда эта поверхность будет наклонена к горизонту под углом аш (рис. 2.4, в). В общем случае численное значение угла аш, зависит от коэффициента трення покоя сыпучего материала ап, угловой скорости вращения барабана и коэффициента заполнения его материалом. При малых угловых скоростях вращения барабана (меньше 0,1 от критической) угол аш равен углу трения покоя ап.
Положение системы (рис. 2.4, в) соответствует реальному максимуму потенциальной энергии системы для данного сочетания геометрических и режимных параметров, поскольку большее значение потенциальной энергии системы невозможно, так как неизбежно начнется движение частиц по открытой поверхности и, следовательно, масса системы уменьшится. Напомним, что под системой мы условились понимать совокупность частиц, неподвижных относительно обечайки барабана. Итак, часть частиц начинает двигаться после того, как система достигает определенного максимума потенциальной энергии. Как уже отмечалось выше, с увеличением угловой скорости вращения барабана объем материала, находящегося в поднимающемся слое, а следовательно, и его масса уменьшаются.
|
Рис. 2.4. Схемы к определению значений потенциальной энергии Была выдвинута гппотеза [4] о том, что потенциальная энергия материала, находящегося в поднимающемся слое, при установившемся режиме движения есть величина постоянная, равная потенциальной энергии всего материала в неподвижном барабане, т. е. Mgh = M2glh =...= M, gh, =...= = MJib где M - общая масса материала в барабане; М, - масса материала, неподвижного относительно обечайки барабана; h, - высота подъема центра тяжести материала относительно "нулевого уровня"; hg— высота подъема центра тяжести сегмента материала, когда его открытая поверхность наклонена к горизонту под углом ag (см. рис. 2.4, б). Проверка данной гипотезы осуществлялась на лабораторной установке (см. рис. 2.3) с использованием фотосъемки. Фотосъемка осуществлялась через прозрачный диск. Фотоаппарат ориентировался оптической осью вдоль оси вращения барабана. Время экспозиции подбиралось таким, чтобы на негативах движущиеся частицы оставляли след в виде штриха. Полученные негативы проецировались на экран, где визуально определялась граница раздела слоев. Планометрированием определялась площадь, занимаемая поднимающимся споем. Вычислялись масса материала поднимающегося слоя, высота |
подъема центра тяжести и далее потенциальная энергия. Контроль за точностью определения границы раздела слоев осуществлялся выборочно, с использованием скоростной киносъемки
Статистическая обработка результатов эксперимента осуществлялась по общепринятым методикам [8]. На рис. 2.5 показаны характерные результаты определения потенциальной энергии поднимающегося слоя при различных угловых скоростях вращения барабана. В качестве сыпучего материала в данном случае использовались стеклянные шарики. Как видно из графика, при установившемся режиме движения, в данном случае при со / С0кР от 0,1 до 0,5, потенциальная энергия поднимающегося слоя практически постоянна и равна реальному минимуму потенциальной энергии (на рис. 2.5 реальный минимум показан сплошной линией). Во всех опытах расхождение значений реального минимума и экспериментальных значений потенциальной энергии не превышало 5 % и объяснялось в основном погрешностью измерений.
Результаты проведенных исследований позволяют сделать выводы:
а) для сыпучего материала, находящегося в превалирующем гравитационном поле, характерны два энергетических уровня - минимальный и максимальный;
б) система, состоящая из частиц, неподвижных относительно друг друга и совершающих движение в плоскости действия гравитационных сил, стремится, а при установившемся движении достигает возможного минимума потенциальной энергии за счет уменьшения своей массы путем перевода частиц за границы системы, т. е. в состояние движения относительно этой системы.
Я, Дж -
![]() ______ о
______ о
о
0,1
_|______ I_____ I_____ I____ I______
0, 1 0,2 0,3 0,4 0,5 ю/Юкр
Рис. 2.5. Зависимость потепциальпой эпергии материала
подпимающегося слоя от скорости вращепия барабапа
Наиболее наглядно это свойство сыпучих материалов проявляется при их движении в поперечном сечении гладкого вращающегося цилиндра. С увеличением угловой скорости вращения цилиндра неизбежно увеличивается высота подъема центра тяжести системы, поэтому для достижения устойчивого состояния система уменьшает свою массу, переводя большее количество частиц в скатывающийся слой, т. е. в состояние движения относительно системы.
Этот эффект саморегулирования наблюдается в довольно широком диапазоне изменения угловой скорости вращения цилиндра. Следует также особо отметить, что система переходит от состояния покоя к движению только после того, как достигнет максимального уровня потенциальной энергии, т. е. перейдет энергетический барьер.