ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПРОЦЕССА ДВУХСТАДИЙНОЕО ДО­ЗИРОВАНИЯ

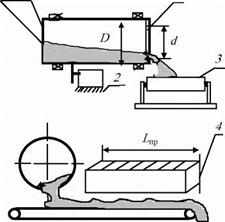
Исследования процесса двухстадийного дозирования проводили на лабораторном барабанном доза­торе, схема которого представлена на рис. 8.18.

Была предусмотрена возможность установки сменных труб 1 с внутренними диаметрами D от 0,042 до 0,15 ми длиною А от 0,1 до 0,45 м. Привод 2 позволял изменять угловую скорость вращения барабана в диапазоне 0,1...0,5 от критической. Диаметр диафрагмы, установленной на выходе из трубы, мог изме­няться в диапазоне (0,4... 1,0)D. Подвижная платформа, на которой установлен барабан 1, шарнирно со­единена с основанием с возможностью изменения угла наклона оси вращения барабана в диапазоне от - 5 до +15°. Для отбора проб использовали подвижный пробоотборник в виде ленточного транспортера 3, что позволяло отбирать пробы за короткие (5 - 10 с) промежутки времени.

Основное внимание уделяли исследованию точности непрерывного дозирования. Методика прове­дения экспериментов следующая. Подготавливали порции сыпучего материала весом АР, которые через равные промежутки времени А Рвысыпали во вращающийся барабан 1. С помощью секционированного пробоотборника 4 сыпучий материал, находящийся на ленте, разделяли на порции. Каждая порция со­ответствовала количеству материала A Q, высыпавшегося из барабана 1 за отрезок времени

А Рпр=А1р/(Мт),

где Lap - длина пробоотборника, м; v - скорость ленты, м-с-1; N - число секций в пробоотборнике. На первом этапе задача заключалась в идентификации параметров математической модели эксперимен­тальным данным. Для конкретного сыпучего материала при фиксированных значениях R, L, со, А Дф проводили несколько серий параллельных экспериментов и методом последовательных приближений рассчитывали такие значения параметров математической модели, при которых расхождения между расчетными значениями A Q и экспериментальными данными были минимальными.

Рис. 8.18. Схема исследования точности дозирования

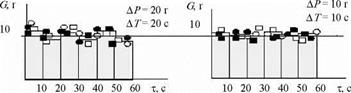
Следующий этап исследования - проверка адекватности математической модели эксперименту. На данном этапе опыты проводили на материалах, для которых были идентифицированы параметры мате­матической модели при различных комбинациях параметров АР, А Т, со, L, R, ос, с/2. Порядок проведения опытов соответствовал описанному выше. На рис. 8.19 показаны характерные зависимости равномерно­сти непрерывного потока от режимных параметров работы устройства. На графиках показаны отклоне­ния от заданной производительности непрерывного дозирования 1 г/с при подаче отдельных порций во вращающийся барабан через промежутки времени АТ, равные соответственно 60, 30, 20 и 10 с. Гисто­граммы - это расчетные значения производительности, а точки - экспериментальные данные.

Как видно из графиков, при уменьшении АТ отклонения от заданной производительности за 10 с уменьшаются, однако точность дозирования при отборе проб за 60 с становится хуже. Аналогичные за­кономерности были экспериментально установлены и при изменении геометрических параметров доза­тора. Таким образом, при расчете оптимальных геометрических и режимных параметров трубчатых до­заторов необходимо учитывать методику оценки точности непрерывного дозирования, которая опреде­ляется потребителем.

Рис. 8.19. Изменения нроизводительности непрерывного нотока во времени

По результатам теоретических и экспериментальных исследований для расчета оптимальных значе­ний основных режимных и геометрических параметров промышленных установок двухстадийного до­зирования сыпучих материалов разработана инженерная методика. Основу методики составляют:

— математическая модель обрушения сыпучего материала при переходе от покоя к движению;

— математическая модель движения сыпучего материала в поперечном сечении гладкого вращаю­щегося барабана;

— математическая модель сегрегации полидисперсного материала;

— математическая модель движения сыпучего материала вдоль оси барабана;

— имитационная модель процесса преобразования отдельных порций сыпучего материала в непре­рывный поток.

В качестве исходных данных используются следующие параметры: производительность, точность дозирования (с указанием временного интервала, в течение которого осуществляется отбор одной про­бы) и основные характеристики сыпучего материала. Расчет осуществляли в два этапа. На первом этапе, исходя из распределения одной пробы, рассчитываются минимальные значения диаметра, длины и час­тоты вращения барабана. На втором этапе рассчитываются оптимальные, с точки зрения обеспечения требуемой точности дозирования, параметры барабана.

[1]

где В= со R cos0 coscp/<7. Параметры |/, 0, Vcp определяли по номограмме.

Время, за которое фронт движущегося материала достигает конца трубчатого дозатора длиной L, определяли по формуле:

t= L/V. (8.34)

Экспериментальная проверка полученной зависимости проводилась в серии опытов на трубчатом дозаторе при угловых скоростях его вращения в диапазоне 0,2 - 0,6 от критической угловой скорости. Коэффициент заполнения изменялся от 0,1 до 0,25. Угол естественного откоса сыпучего материала был равен 45°. В экспериментах использовались трубчатые дозаторы с отношением L/D > 20. Для трубчатого преобразователя отдельных порций в непрерывный поток нецелесообразно использовать такие большие отношения L/D. Учитывая это, несмотря на хорошую сходимость расчетных и экспериментальных зна­чений t (отклонение не превышало 10 %) необходимо экспериментально проверить возможность исполь­зования зависимости (2.26) при L/D< 6.

Проведенный выше анализ показывает, что в настоящее время нет математических моделей, позво­ляющих описать неустановившийся режим движения сыпучего материала вдоль оси вращающегося ба­рабана. Однако очевидно, что скатывание частиц по открытой поверхности и перемещение их вдоль оси трубы происходит по углу максимального ската, поэтому рассмотрим последовательность расчета дан­ного угла. На рис. 8.11 показана схема движения частиц сыпучего материала вдоль оси барабана. Рас­смотрим перемещение частиц с произвольного участка К. Будем считать, что частицы данного участка переходят из поднимающегося слоя в скатывающийся в точку At. Заканчивать свое движение в скаты­вающемся слое частицы будут в точках Вк + 1, Bt + 2 и т. д. до точки Bj, которой соответствует макси­мальный угол ската. На рис. 8.12 показана схема для расчета угла ската - е. Прежде всего необходимо