ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

ДВИЖЕНИЕ МАТЕРИАЛА ВДОЛЬ ОСИ БАРАБАНА

При проектировании новых машин барабанного типа и модернизации действующих необходимо рассчитать производительность, распределение сыпучего материала и время пребывания его в барабане, так как именно эти параметры связывают размеры и режим работы барабана с процессом, реализуемым в нем [1].

Одной из характерных особенностей гладкого вращающегося барабана с подпорными кольцами на торцах является возможность изменения производительности, т. е. транспортирующей способности при постоянных геометрических параметрах барабана и угловой скорости его вращения за счет перераспре­деления сыпучего материала по объему барабана. Исходя из этого можно сделать вывод о том, что если
производительность задается питателем, который подает сыпучий материал в барабан, то расчет сво­дится либо к выяснению, может ли барабан при данных геометрических размерах и угловой скорости вращения обеспечить требуемую производительность и какими будут распределение сыпучего мате­риала и время его пребывания в барабане, либо к определению геометрических размеров и угловой ско­рости вращения, обеспечивающих требуемое время пребывания.

Среднее время пребывания (тс) сыпучего материала в барабане можно определить по формуле:

тс = V/Q, (2.36)

где V- объем материала, находящегося в барабане; Q - объемная производительность.

При заданной производительности вопрос сводится к определению V, т. е. распределению сыпучего материала по объему барабана.

Рассмотрим движение сыпучего материала в гладком вращающемся цилиндре, ось которого накло­нена к горизонту под углом ос. Разобьем барабан по длине на N участков длиной A L и введем нумера­цию участков, начиная от разгрузочного края. Принимаем, что заполнение сыпучим материалом попе­речного сечения барабана, которое будем характеризовать углом 28q/ (см. рис. 2.2), изменяется ступен­чато вдоль оси барабана (j - номер участка).

Будем считать, что за одно пребывание в скатывающемся слое частицы, находящиеся на открытой поверхности, переместятся вдоль оси на расстояние AL. Данное условие всегда может быть обеспечено за счет изменения соотношения заполнения барабана материалом на соседних участках. При построе­нии модели принимаем также следующие допущения:

1) все частицы мало отличаются друг or друга по форме, размерам и плотностям, т. е. рассматривае­мый сыпучий материал не склонен к сегрегации;

2) при движении истирания, дробления и агломерации частиц не происходит.

Рассмотрим два соседних участка j иу + 1.

Как известно [11], движение частиц вдоль оси происходит по линии максимального ската. На рис. 2.6 дана схема для определения угла максимального ската £/, т. е. угла между линией Aj Bj и ее проекцией на горизонтальную плоскость, проведенную через точку О и точку Bj.

Из чисто геометрических соотношений получим:

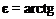yAj+l -yBj)lcosa+]^L-{yAM - yBj)tga sina

(xAj ~ *Bj) + [A2-cos a - {yAj+i - yBj) sin a

У гол Jj отклонения линии максимального ската от плоскости УХО в проекции на плоскость ZOX равен:

t XL

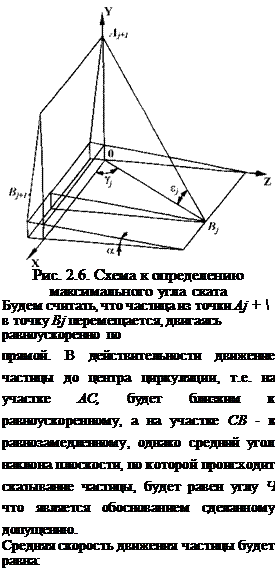
У j = arctg—------------------------------------- т

7фіп(аю 7+1 + 50 7+1) + sin(6n / - суД]

тсру = 0,5 (2.39)

где Lab~ длина отрезка АВ, а, - ускорение движения частицы, a j = gismzj - С coszj) (здесь g - ускорение

свободного падения, ^ - коэффициент трения движения).

Скорость движения частиц по толщине скатывающегося слоя неодинакова и в первом приближении можно записать следующую зависимость:

где і? - текущий радиус движения частицы в поднимающемся слое, Re Rcj ■

Скорость движения частиц вдоль оси барабана в зависимости от радиуса их движения в подни­мающемся слое будет равна:

CJ

В зависимости от радиуса движения частиц в поднимающемся слое изменяется их количество, по­ступающее в единицу времени в скатывающийся слой. Если рассмотреть движение части кольца радиу­сом R и толщиной dR, то можно записать:

dq= o>RdR, (2.42)

где dq - площадь поперечного сечения материала, поступающего в скатывающийся слой в единицу вре­мени с участка границы раздела слоев шириной dR и находящегося на расстоянии R от оси вращения ба­рабана.

С учетом (2.42) средняя скорость скатывающегося слоя в осевом направлении барабана будет рав­на:

После интегрирования формулы (2.43) и несложных преобразований получим:

sinjjpajL^ ■ (6Rs + 4RCJ)

15(Д5+47? )

Расчетная производительность барабана по /-му участку будет равна:

Q^-C.-NALv^:. (2.45)

С другой стороны, производительность (Q.) барабана задана и должно выполняться равенство:

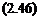
<?Р/=а-

При заданных или принятых диаметре барабана, угловой скорости его вращения и угле наклона оси к горизонту численные значения CjNj и іср ос / зависят от AL и коэффициента заполнения барабана ма­териалом нау-м участке (280у). Следовательно, задавшись величиной ДА, можно всегда найти такое зна­чение 280у, при котором выполняется равенство (2.46).

С учетом изложенного выше последовательность расчета распределения сыпучего материала и времени его пребывания в барабане следующая. Исходя из радиуса отверстия подпорного кольца, уста­новленного на разгрузочном краю барабана, диаметра барабана, угловой скорости его вращения и фи­зико-механических характеристик сыпучего материала рассчитывается заполнение барабана материа­лом на первом участке, т. е. определяется величина 28от При этом должно выполняться условие, что Rc = RK, где RK - радиус отверстия подпорного кольца. В качестве физико-механических характеристик сыпучего материала используются углы и коэффициенты трения, движения и покоя. Определение чис­ленного значения угла 28oi может быть выполнено путем последовательного увеличения 28оі. от вели-

чины 2arccos— до тех пор, пока Rcl не станет равным RK.

R&

Далее рассматривается второй участок. Задается значение 28о2 = = 25оі + /Або и рассчитывается значение Qp2, при этом і изменяется от 1 до п до тех пор, пока не будет выполняться равенство (2.46). Изменяя значение j от 1 до N, где N - количество участков по длине барабана, рассчитывают распреде­ление сыпучего материала по объему барабана. Объем материала, находящегося на у-м участке, можно определить по следующей формуле:

V) = 0,5^(280,--sin 28oy)AL. (2.47)

Общий объем материала в барабане будет равен:

V=YVJ - (2.48)

7=1

Зависимости (2.36) - (2.48) представляют собой математическую модель процесса распределения и движения сыпучего материала в гладком вращающемся барабане. Адекватность предлагаемой модели проверена экспериментально на лабораторной установке с барабаном диаметром 0,25 м и длиной 0,4 и 0,6 м. Угловую скорость вращения барабана изменяли в интервале 0,1...0,6 от критической. В качестве
сыпучего материала использовали дробленый кварц с частицами размером 0,5 мм и гранулированный по­лиэтилен с частицами диаметром 2 мм.

Расчетный объем материала, находящегося в барабане, отличался от определенного эксперимен­тально не более чем на 5... 10 %, а расхождение экспериментальных и расчетных значений времени пребывания меченых частиц в барабане не превышало 15...20 %.

Движение сыпучего материала во вращающемся барабане с эллиптическим поперечным сечением рассмотрено в работе [16], осевое движение в работах [17 - 19]. Результаты данных исследований были положены в основу методик расчета режимов движения сыпучих материалов в гладких вращающихся барабанах [20 - 22].

В последние годы для расчета параметров движения и распределения сыпучих материалов во вра­щающихся барабанах используются компьютерные технологии [23], что существенно упрощает задачи проектировщиков при определении оптимальных геометрических и режимных параметров машин бара­банного типа.