Оптоэлектроника

Условия оптического усиления в полупроводниках

Анализ, проведенный в разделе 7.3 показал, что полупроводник, выведенный из состояния термодинамического равновесия, может обеспечить условия оптическо­го усиления фотонов с энергией, удовлетворяющей условию Бернара—Дюррафура (1.266). Таким образом, представляется важным раскрыть особенности экспери­мента, обеспечивающие реализацию этого условия.

Предположим, что в неравновесных условиях вводится значительное число носите­лей (Ап и Др) Так, что положение квазиуровней Ферми дается соотношениями:

ЕРс = Ес + кТЕ1/2

(7.67)

Ег„ = £■„ - кТР1/2

Где Е1/: есть функция, обратная интегральной функции Ферми—Дирака порядка 1/2, определяемой (смотрите раздел 5.6) как:

(7.68)

Предположим, что полупроводник слегка легирован и что п = р » п0 и р0. В этом случае материал более не будет поглощать фотоны с энергией Иу = Е в том случае, когда неравновесная концентрация носителей я1гап5р будет удовлетворять сле­дующему условию прозрачности (смотрите (7.626)):

(7.69)
	> 0

Условие прозрачности для полупроводника

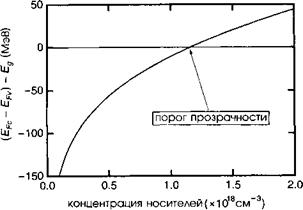
Рисунок 7.6 демонстрирует разность ЕРс — ЕРу) в функции неравновесной концен­трации носителей п. Концентрация прозрачности достигается, когда ЕРс — ЕРу) = Е, что эквивалентно условию прозрачности (7.69)

Пример--------------------------------------------------------------------------------------------------------------

Программа МАТНЕМАТ1СА, приведенная ниже, дает пример поведения квази­уровней Ферми в СаАБ в функции неравновесной концентрации носителей. Усло­вие прозрачности реализуется при я1гап5р = 1,2 х 1018 см-3.

0атт32=8дП[11[РШ/2

Р[х_,и_]=8дП[х]/(1+Ехр[х-и])

ТОегт1=ТаЬ1е[{Мтедга1е[1[х, и],{х,0,1п1тйу}]/датт32,и},{и,-5,5,0.2}]

Иегт1=1п1егро1айоп[й1егггп]

11с=4.7*1(Г17(*т ст-3*)

N№=7 1(Г18(*т ст-3*)

Е*с [ п Л=1 е гт I [ п/Ы с]

ЕМР_]=11егпгп[р/1№]

Deltaef[xJ=25.9*(efc[x]+efv[x])

Plot[deltaef [х], {х, 1 (Г 16,2" 18} ]

Выше порога прозрачности среда начинает усиливать те фотоны, которые обладают энергией, удовлетворяющей условию Бернара—Дюррафура. В этом случае спектр усиле­ния дается соотношением:

Г(Ьу)= к, ъЛн'' - £,«)1/2[Л(А*/)-Л(л*/)]

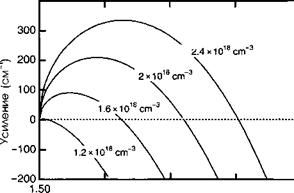
Где КаЫ дается (7.52б), а функции Ферми— Дирака /с(Иу) и /ДЛг) определяют засе­ленность тех уровней в зоне проводимости и валентной зоне, которые удовлетво­ряют условию Ес — £ = Иу и которые даются соотношениями (7.25я) и (7.25б). Рисунок 7.7. показывает, каким образом кривая усиления изменяется в функции неравновесной концентрации носителей в ваАз. Чем больше превышение концен­трации носителей порога прозрачности, тем шире становится кривая усиления. Рисунок 7.8 показывает, каким образом максимальное усиление изменяется в фун­кции неравновесной концентрации носителей. После достижения прозрачности максимальное усиление увеличивается линейно с возрастанием плотности заряда над порогом. Это чисто феноменологическое соотношение очень полезно при мо­делировании полупроводниковых лазеров (смотрите главу 13).

Пример--------------------------------------------------------------------------------------------------------------

Ниже приведена программа МАТЕМАТ1СА, описывающая поведение усиления в неравновесном полупроводнике. Рекомендуем читателю потренироваться в исполь­зовании этой программы с применением численных постоянных для различных полупроводников, приведенных в таблице приложения (стр. 588).

Оатт32=8дП[11[РШ/2;

Р[х_,и_]=8дП[х]/(1+Ехр{х-и]);

А1егтИТаЬ1е[{Мт1едга1е[1[х, и],{хД1п1тйу}]/датт32,и},и,-5,5,0.2}]

Йегпгп =ТаЬ1е[{Мт1едга1е[1[х, и],{хД1п1тКу}]датт32,и},{и,-5,5,0.2}]

11егтМп1егро1айоп[й1егпгп];

300

2

О,

Ф

S

I

5

О

Рис. 7.8. Изменение максимума кривой усиления в ваАБ в функции концентра­ции электронно-дырочных пар.

Kb=8.63 10" -5;Т=300;

Nc=4.7* 10" 17 (*in cm-3);Nv=7. 10" 18 (*in cm-3*); Eg=1.5;mc=0.067;mv=0.46;Kabs=12000; mr= 1 /(1 /mc+1 /mv); n=1.2 10" 18;

Nc=n/Nc;efc=25.9 10"-3*ifermi[nc] nv=n/Nv;efv=25.9 10" -3*ifermi[nc] nv=n/Nv;efv=25.9 10" -3*ifermi[nv] Ec=mr/mc*(hnu-Eg);

Ev=mr/mv*(hnu-Eg); fc=1/(Exp[Ec-efc)/kb*T)]+1); fv— 1 /(exp [Ev+efv)/kb*T)]+1); gain-Kabs*(hnu-Eg)(1/2)*(fc-fv); plot12=Plot[gain,{hnu,1.5,1.6}]