Условия достижения порога в VCSEL
Функциональные характеристики VCSEL мы можем легко оценить, отправляясь от ряда простых рассмотрений. VCSEL может быть аппроксимирован резонатором
|
Брэгговское зеркало М--------------------------------------------------------------- ► QW
Ueff |
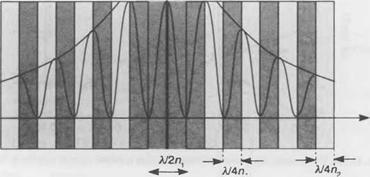
![]() Рис. 13.В.1. VCSEL, состоящий из квантовых ям, выращенных в резонаторе Фабри— Перо, заключенных между двумя брэгговскими зеркалами. Рисунок показывает распределение электромагнитного поля в резонаторе.
Рис. 13.В.1. VCSEL, состоящий из квантовых ям, выращенных в резонаторе Фабри— Перо, заключенных между двумя брэгговскими зеркалами. Рисунок показывает распределение электромагнитного поля в резонаторе.
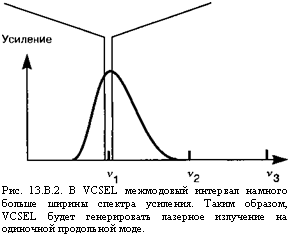
Фабри—Перо толщиной L = 1/2п^, заключенным между двумя металлическими зеркалами. В этом случае межмодовый интервал составляет Av = c'/2L = с'/Л(с' =c/nsc), т. е. A hv= 1,6 эВ для L = 0,16 мкм и в предположении типичных величин «5с = 3и Л = 1 мкм. Поскольку этот межмодовый интервал намного больше ширины полосы усиления, лазер работает на одиночной продольной моде (смотрите рис. 13.В.2).
В этом случае порог лазерной генерации дается выражением:
|
-In |
![]()
|
Fyth |
![]() 1 ■ - 1 1
1 ■ - 1 1
I' Threshold
An +
Ят1Ят
Здесь Ят1, Тт1, Ят2 и Тт2 есть соответственно коэффициенты отражения и пропускания для верхнего и нижнего зеркал, ар есть паразитное поглощение, Г — коэффициент перекрытия между электромагнитной волной и квантовой ямой. ЬеЯ. — эффективная длина резонатора: в УС8ЕЬ она включает в себя расстояние, на которое волна проникает в брэгговское зеркало или, иначе говоря, на которое фотоны проникают в зеркала за счет туннелирования. Расчет и не является простым, но величина этого параметра не является первостепенным фактором в нашей попытке оценить функциональные характеристики УС8ЕЬ.
Принципиальные аспекты УС8ЕЬ в сжатом виде заключены в (13.В. 1): хотя коэффициент перекрытия Г достаточно мал, это может быть компенсировано использованием зеркал с малым пропусканием. У нас есть возможность оценить каждый из приведенных параметров. Коэффициенты пропускания Тт брэгговских зеркал были рассчитаны в дополнении 9.Г (смотрите (9. Г. 39)):
1-
|
(13.В.2) |
![]()
|
71 = 1 - |
![]() F 2N П2
F 2N П2
|
Здесь л] и п2 коэффициенты преломления слоев, образующих брэгговские зеркала. Коэффициент перекрытия Г определяется интегралом: |
![]()
1 +
Пропускание
|
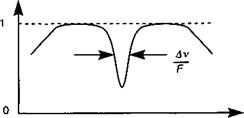
Рис. 13.В.2. В VCSEL межмодовый интервал намного больше ширины спектра усиления. Таким образом, VCSEL будет генерировать лазерное излучение на одиночной продольной моде. |
99%
|
_ -d/2 |
![]()
|
Г = |
![]() (13.B.3)
(13.B.3)
Здесь с1 — толщина активной области. Для оценки этого интеграла мы использовали аппроксимацию (9.Г.26), заключающуюся в том, что поле Е(1) рассматривается как стационарная волна:
|
(13.В.4) |
![]() £(*)=£„ cosf^) - / 2 < z < LtSf /2
£(*)=£„ cosf^) - / 2 < z < LtSf /2
В других областях Е(і) =0. В рамках этой аппроксимации мы пренебрегаем электромагнитным полем за пределами расстояния туннелирования фотонов в брэгговских зеркалах. В этом случае интеграл (ІЗ. Г.З) легко рассчитать:
|
DEl |
![]()
|
Г = |
| Е] cos2 (rcz / Lcff)dz
Это приводит к:
|
(13.В.6) |
![]() D
D
Г = *7 *7
Здесь: /7 = 2 для аппроксимации (13.Б.4), но в общем случае имеет значение в диапазоне от 1 до 2. Интеграл (13.В. З) показывает важность расположения уси-
Лителя по отношению к пучности электромагнитной волны. Если бы квантовая яма располагалась в узле электромагнитной волны, то эффективное усиление Гу было бы равно нулю. Этот результат мог бы быть получен с использованием соотношения (4. В. 12) (полученного при изучении электромагнитных лазерных уравнений в дополнении 4.В) т. е. с применением (13.В.4) для E(z) как для единственной допустимой моды резонатора. При подстановке (13.В.5) в (13.В.1) и пренебрежении паразитными потерями находим, что необходимое усиление у порога составляет:
Тт 1 + Тт1 = 277D}
Threshold
(13.В.7)
Пороговое условие для VCSEL
Теперь мы можем определить типичные условия функционирования VCSEL. Сконцентрируем свое внимание на системе GaAs/AlGaAs, поскольку она является наиболее употребимой системой для изготовления таких приборов. Предположим, что активной областью нашего VCSEL является квантовая яма толщиной 100 А (id = 10"6 см). Предположим, что мы хотим добиться, чтобы пороговый ток для прибора с площадью активной области 30 х 30 мкм2 составил 1,2 мА (т. е., что плотность порогового тока /threshold =136 А/см2). В предположении, что время жизни составляет 1,6 не это приводит к двумерной концентрации носителей ns = /threshold t{Jq или 1,36 х 1012 см"2 (смотрите (13.3)). В этом случае пороговое усиление дается (13.57) и составляет:
Dr„ = A2D( - е-А'*-) (13.В.8)
Здесь коэффициенты a2Bd = A2D = 0,55%, пс = 7,25 х 1011 см"2, a Rcv = 6,8 получен в примере раздела 13.6.1. Это приводит к *tyhreshold = 4,9 х 10"4or2D, т. е. threshold = 490 см-1. В этом случае уравнение (13.В.7) дает сумму Тт1 + Тт2 величиной 9,8 х 10"4. Полагая ТтХ = Тт2 и используя (13.В.2), мы видим, что мы можем выбрать набор, состоящий из 30 пар слоев GaAs/AlAs для нижнего зеркала и 30 пар слоев для верхнего зеркала (в дальнейшем будем полагать Л~ 1 мкм, п{ = 3,4 и п2 = 2,96).
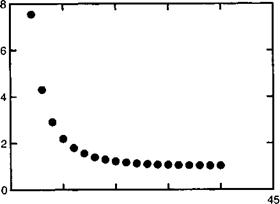
Рисунок 13.B.3 показывает расчетное убывание порогового тока в функции числа пар слоев в брэгговских зеркалах.
|
|
|
Л Ш О I— О Q. О С |
|
25 30 35 40 Число пар слоев брэгговских зеркал |
|
Рис. 13.В. Э. Изменение порогового тока УС8ЕЬ на основе ОаАз/АЬАБ в функции числа пар слоев в брэгговских зеркалах (5 = 30 х 30 мкм2). |
|
|