Оптоэлектроника

Уравнения переноса в полупроводниках

В принципе, полуклассическое описание явлений переноса в полупроводниковом приборе должно было бы иметь вид уравнения Больцмана, включающее все электро­ны в зоне проводимости и валентной зоне. При этом в интеграле столкновений следовало бы детализировать все соответствующие взаимодействия, включая те, ко­торые приводят к рассеянию электронов между зонами, что соответствует процессам генерации и рекомбинации. К этому уравнению следовало бы еще добавить уравне­ния Максвелла для полей, ответственных за силы, действующие на электроны.

Естественно, с такими уравнениями справиться очень сложно. К тому же полу­ченные результаты не носили бы детальный характер. Таким образом, более пред­почтительным является возврат к уравнениям, по своей природе более общего харак­тера и которые к тому же частично являются феноменологическими.

Первыми уравнениями являются уравнения непрерывности, получаемые из урав­нения Больцмана интегрированием функции распределения по всем состояниям к и выделением электронной и дырочной составляющих:

(6.60)

Полупроводниковое уравнение 1: уравнение непрерывности

Где <7 и Я есть соответственно скорости генерации и рекомбинации, при этом плотности электронного и дырочного тока составляют соответственно ]п = — пе (п) и }р = Ре (Ур)- Для плотностей тока мы используем уравнения:

І = ей пЕ + ей V«

Лп • п п

Р = - еОУр

Полупроводниковое уравнение 2: законы Ома и Фи ка

Эти уравнения выведены под влиянием результатов, полученных в разделе 6.1 для слабых полей и малых градиентов, в то время как значения подвижности и коэффициентов диффузии являются параметрами, полученными либо эксперимен­тально, либо численным решением уравнения Больцмана. Отметим также, что на­пряженность электрического поля, обозначаемая в этих уравнениях как Е, не сле­дует путать с энергией. В зависимости от допустимой степени усложнения модели мы можем также ввести в нее зависимости для //„(£) и т. д., а также учесть эффекты с участием горячих электронов.

К уравнениям, описывающим реакцию частиц на воздействие полей, следует доба­вить уравнения Максвелла, определяющие зависимость полей от параметров среды:

	(6.62) (6.63) (6.64)

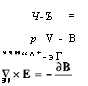Где для немагнитных полупроводников В = //0Н и В = еЕ, а е есть проницаемость, связанная с поляризацией локализованных зарядов.

В большинстве проблем переноса в полупроводниках значвения длин волн, связанные с соответствующими частотами, намного больше размеров приборов, где магнитные поля не играют особой роли. В этих случаях важными являются урав­нения Пуассона (6.62) V • Е = р/е, а также тот факт, что полный ток = }соп6 + Э В/Э/ сохраняется при условии, что его дивергенция равна нулю в соответствии с (6.64).

Плотность заряда определяется соотношением р= е(р — п + Л^+ — Л^~), где М* есть концентрация ионизированных доноров, а Л^~ — концентрация ионизирован­ных акцепторов.

Приведенные уравнения создают основу для описания классических полупро­водниковых приборов, (т. е. транзисторов, фотодиодов, фоторезисторов и т. д.). Эффекты, проявляющиеся на шкале длин, соответствующей волновой природе элек­тронов, скрыты в параметрах этих уравнений или в членах — источниках, подоб­ных скоростям генерации носителей при поглощении фотонов и т. д.

Рассмотрим теперь важное применение этих уравнений. В разделе 6.3 мы столк­нулись с дебаевской длиной (уравнение (6.24)), представляющих собой характерис­тическую протяженность, в пределах которой свободные электроны могут экраниро­вать слабый возмущающий потенциал за счет обеднения, либо аккумуляции элект­ронов. Во многих приборах мы прикладываем достаточно сильные потенциалы (» квТ), способные полностью привести электронный газ в режим обеднения в области локализации потенциала (которая в этом случае характеризуется плотностью заряда, связанного с ионизированными донорами). Оценка уравнения Пуассона для этого случая приводит к другой длине экранировки, называемой длиной обеднения.

Представим себе легированный полупроводник с концентрацией доноров и кроме того предположим, что при I = 0 электрическое поле «толкает» электроны в направлении г > 0. В области 0 < z< 16ер практически не будет электронов (смотри­те рис. 6.12). При этом уравнение Пуассона может быть записано в виде:

С1Е еМо

-7х =------- 0<Z<ZІ'P (6.66)

<21 £

Оно может быть легко проинтегрировано, что дает:

ЕЫ +

Ег=-Е,+^1 (6.67)

Зона обеднения простирается вплоть до точки, где Е =0:

= тщ; (6'68)

При этом падение потенциала в этой области составляет:

Г(ь*)-У(0)=^-г1Р (6.69)

Таким образом:

12еАУ.....

Г*Р у еМ, (6.70)

Глубина обеднения

Глубина обеднения является важным параметром, так как она определяет про­тяженность области, в пределах которой падает потенциал в легированном полу­

Проводнике. Мы видим, что этот параметр принимает значение дебаевской длины, если мы заменим 2ДКна квТ/е; предположение, что еАУ» квТозначает, что zdep » Х0. В действительности, переход от области обеднения к нейтральному полупроводни­ку не является резким, но простирается на длину порядка Хв относительно zdep^

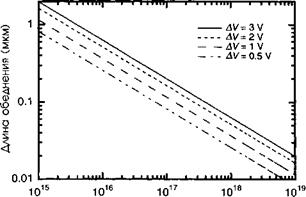
Рисунок 6.13 демонстрирует толщину области обеднения для ряда случаев.

£

О.

ИГ

ИГ

О.

Ш

X

О

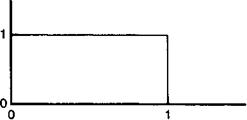
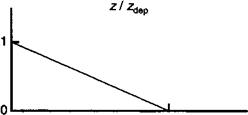
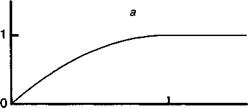
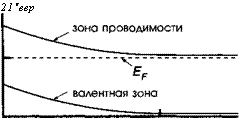
Рис. 6.12. Распределение заряда р (а), электрического поля Е(б), электростатического потенциала К (в) и зонной диаграммы в области обеднения ^ер дается урав­нением (6.68).

Пример--------------------------------------------------------------------------------------------------------

Полагая, что ДК = 1 В и ND = 1017 см-3, получаем для GaAs:

2eAV 2x12x8,8х10-,2х1 Л11

1,6хЮ-»х10"