Оптоэлектроника

Уравнение Больцмана

В главе 5 мы видели, что движение электронов в пределах полупроводниковой зоны под воздействием электрического поля Р можно представить как изменение состояний в зоне, которое определяется выражением:

|я(к, /)|2 - а К - , О

I й

Это означает, что, если в момент времени / = 0 электрон находится в состоянии к, то затем в момент времени / он будет находиться в состоянии к + с^г/Ь. Напом­ним, что это обстоятельство лежит в основе феномена блоховских осцилляций. Другим образом влияние электрического поля может быть описано уравнением:

(6.2)

&

Эта формула аналогична закону Ньютона, если рассматривать Ь к как квазиимпульс. В ре­альном пространстве скорость электрона в состоянии к определяется групповой скоростью:

У(к) = -Ук£(к)

П

Где мы можем предположить, что обратная матрица М~1 для эффективной массы не зависит от к вблизи энергетических экстремумов в обратном пространстве. Такой подход справедлив в случае идеального полупроводника (как и для других кристал­лических твердых тел) с тем ограничением, что электрическое поле достаточно сла­бо, чтобы вызвать межзонные переходы, а также что рассеянием на несовершен­ствах (фононы, примеси и т. д.), приводящим к переходам между различными к-состояниями, можно пренебречь (последнее требование в общем случае не выпол­няется, и оно жестко ограничивает реализуемость этого подхода на практике).

С другой стороны, такое описание формирует основу полуклассической аппрок­симации явлений переноса. В этом случае реакция электрона (расположенного в момент / в точке г полупроводника и в состоянии к зоны п) на воздействие локаль­ного поля Е(г) определяется соотношениями (6.1)—(6.4). Отклонения от идеально­го случая (из-за примесей, колебаний решетки, дефектов...) вызывают переходы между к и к' и не сопровождаются изменением положения частицы. Понятно, что такой подход является всего лишь аппроксимацией, так как в квантовой механике невозможно одновременное задание скорости и положения электрона (с любой точностью), а также вследствие того, что само понятие состояния к не имеет точно­го смысла за исключением бесконечно протяженного полупроводника. Несмотря на эти ограничения, указанный подход достаточно корректен до тех пор, пока из­менениями интересующих нас параметров (например, напряженности поля, ...) на длине, равной или большей среднего расстояния между двумя событиями рассея­ния, которое испытывает электрон, можно пренебречь. Ограничимся этим и не будем приводить здесь более детальное обоснование справедливости полукласси - ческого подхода. Очевидно, что в случае квантовой ямы полуклассическое прибли­жение не является допустимым при рассмотрении движения электрона перпенди­кулярно границам раздела. В самом деле, основной отличительной особенностью полуклассической аппроксимации является то, что волновая природа электрона учитывается лишь косвенно через зонную структуру в виде Е(к) и через процессы рассеяния, которые рассчитываются как вероятности переходов в единицу времени (определяемые золотым правилом Ферми) с использованием волновых функций в начальном к и конечном к' состояниях. В этом случае ансамбль электронов в зоне может быть описан функцией распределения Дг, к, /)> описывающей либо вероят­ность найти электрон в момент времени / в положении г и состоянии к, либо число электронов в объемном элементе сРгсРк фазового пространства. Эти две возмож­ные интерпретации связаны друг с другом плотностью состояний ^с!3г/(2я)3, где ^ = 2 — вырождение электронов по спину.

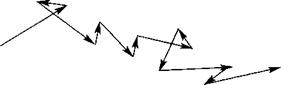
Характер изменения Дг, к, 0 в промежуток времени от / до / + с1/ и в отсутствие каких-либо столкновений можно описать, рассматривая объем фазового простран­ства в момент времени / + & (рис. 6.1).

Теперь частицы, которые находятся в точке (г, к), изначально в момент време­ни / находились в точке (г — ус!/, к — (ёк/ёО^О и, таким образом, испытали дрейф:

А

Г

Рис. 6.1. Орбиты группы частиц в фазовом про - странстве между моментами времени /0 и /1 и в отсутствие столкновений.

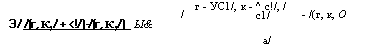С! к

= - у(к) • Уг/(г, к, 0 - — • Ук/(г, к, О

К частицам, продрейфовавшим к точке (г, к) мы должны прибавить чистое число частиц, введенных в эту область фазового пространства из-за столкновений из состояний к':

^ 1 = У £(к' -> к)/(г, к', I) - 5(к к')/(г, к, О

& Ь>п к'

Где ^(к' —»к) есть вероятность в единицу времени того, что переход происходит между со­стояниями к' и к.

Уравнение, описывающее изменение /, под комбинированным воздействием электрического поля и столкновений дается, таким образом, соотношением:

^ + у(к)Уг/+-^Ук/ = Э/ й

Уравнение Больцмана

Это уравнение, называемое уравнением Больцмана является очень важным, так как устанавливает взаимосвязь квантовых и классических аспектов поведения элек­тронов в твердых телах. Как только становится известным решение /(г, к, /) этого уравнения, мы можем рассчитать такие средние макроскопические параметры, как концентрацию носителей:

П(Г, 0 = |

(6.8)

•/(г, к, 0

Плотность тока:

(6.9)

Среднюю кинетическую энергию частиц:

(£(г, /)) = —!— [М^£(к)/(г, к

«(г, /) J {2я)

А также дисперсию скорости:

Ст2 (г, о = —Г(к) - (у)21/(Г, к, Г) (6.11)

И(г, 01 (2л) I - I

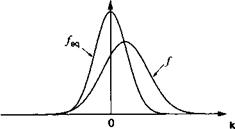
Уравнение (6.7) в сочетании с членом столкновений (6.6) обладает малым практичес­ким значением. Теперь попробуем получить несколько простых решений уравнений Боль­цмана. Сначала предположим, что интеграл столкновений можно аппроксимиро­вать с использованием одного времени релаксации (зависящего только от энергии состояния к), стремящейся привести распределение обратно к виду^ч(г, к, /) (смот­рите рис. 6.2), т. е.:

/(г, к, Г) - /е8(г, к, О г(£(к))

Рис. 6.2. Функции распределения в состо­янии равновесия (/^(к)) и под влиянием электрического поля (Дк)).

Аппроксимация в виде (6.12) имеет чрезвычайную физическую значимость. В то время как все уравнения переноса, введенные нами до сих пор, инвариантны по отно­шению к обращению времени, уравнение (6.12) вводит предпочтительное направление («стрелу времени»). Многие связи между микроскопической теорией материи и мак­роскопической термодинамикой скрыты в этом уравнении. Это последняя аппрокси­мация означает, что как только возмущающее электрическое поле выключается, фун­кция будет экспоненциально по времени релаксировать к своей первоначальной фор­ме с временем релаксации т{Е). Отыскивая стационарное решение, близкое к функции распределения, с помощью итераций мы находим функцию распределения:

/ г /« - т(£(к))|у(к) • + д¥ ■ Ук/е,]= /„ - г(£(к))

ЪЕ (6.13)

С использованием этого последнего выражения получаем для средней скорости:

Э4 ДЕ

(У(г)) = -

(6.14)

В случае простого невырожденного полупроводника при температуре Т или /еч~ ехр(~Е/квТ), где кв — постоянная Больцмана и в предположении у(к)= Ьк/т' можем переписать уравнение (6.14) в виде:

V,«

(▼(г)) = /«р - 0

Где /г — подвижность, определяемая соотношением:

9

|у2гехр{-[£(к)Мв:Г]}(13к

3 квТ | ехр{-[£(к) / А:я7’]}<1 Зк а /)— коэффициент диффузии:

, [ у2гехр{-[.£(к)/А:в7’]}с1 Зк

3 |ехр{-{£(к)/*,Г]}<13к

Сравнивая эти два последних уравнения, мы находим следующее отношение Эйнштейна, связывающее подвижность и диффузионный перенос:

(6.18)

Соотношение Эйнштейна

Возвращаясь к (6.15), мы видим, что ток определяется суммой двух Кг) = ?я(г)(у(г)> = яп(г)м¥ ~ яПЧгп(т) что может быть записано (смотрите рис. 6.3) в виде:

КГ) = ^сопс!^) •ЬиП‘(Г)

F

---------------- ►

Ток проводимости ]сопс1 есть ток, описываемый законом Ома:

^о„А) = (6-20а)

Где а — есть электропроводность, которая связана с подвижностью соотношением:

А = (6.206)

Плотность диффузионного тока ^ связана с перемещением носителей в обла­сти структуры с меньшей концентрацией носителей и дается законом Фика:

Ыг> = ~я№п (6.21)

Закон Фика

Замечание: С учетом # = — е в нашем определении электронной подвижности эта величина является отрицательной. Более общепринятым однако является использование аб­солютных величин для # и //, что делает необходимым изменение знака перед // в уравнении (6.15).

Особо важный случай имеет место, когда занятыми являются только состояния вбли­зи энергетического минимума, когда эффективная масса вблизи минимума являет­ся изотропной (Дк) = Ь2к2/2т* + Ес). В этом случае подвижность может быть запи­сана как функция определенной средней величины г для кинетической энергии:

|£3/2г(£)ехр[- (Е /кВТ)$Е И = (6-22)

ЪкгЛт л г, ...

|Е'12 ехр[-(£/^Г)]с!£

О

Если время релаксации не зависит от энергии Е, это последнее выражение сводится к простой модели Друде, при этом:

М = Я~^т (6-23 а)

Т

Подвижность (см2 В-1 с-1) в модели Друде

В более общем случае, когда т(Е) = т0(Е/Е0)а, уравнение (6.22) принимает вид:

Ц-ЧФ, ТУ 2г[(5/2)+«]

А--------------------- 7^— з~^?72Г (щ

Где Г есть гамма-функция, Г(1/2) = Г(х + 1) = хГ(х).

Пример------------------------------------------------------------------------------------------------------------------------------------------------ —-

При температуре 300 К арсенид галлия, легированный до концентрации 1015 см-3 имеет время релаксации 0,3 пс. При использовании формулы Друде ожидаемая под­вижность электронов должна составлять 1,6 х 10~19 Кл х 3 х 10-13 с/(0,067 х 0,9 х 10“30 кг) или 8000 см2 В-1 с-1.