Оптоэлектроника

Тепловые аспекты лазерных диодов и мощных приборов

Одной из особенностью лазерных диодов по сравнению с газовыми или ионными лазерами с твердотельной матрицей (как например Nd: YAG) является то, что ак­тивный объем, в котором носители рекомбинируют (излучательно или другим об­разом), занимает незначительную часть структуры. Таким образом, лазерный диод с квантовой эффективностью rj = 1 — £ < 1 рассеивает в виде тепла %Р от полной мощности в малом объеме материала. Это может приводить к существенному на­греву материала, что может привести к нарушению функциональных характерис­тик прибора и, в конечном результате, к его отказу (химическая деградация, рас­плавление и т. д.). Сейчас мы изложим краткий теоретический подход, в рамках которого мы сможем исследовать нагрев и его влияние на характеристики лазебр - ных диодов. Для простоты ограничимся одномерной моделью.

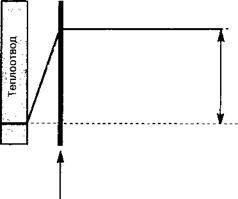
Нашей исходной точкой будет закон Ньютона—Флика, устанавливающий, что тепловой поток Ф (Вт) через границу материала, обладающего неоднородным рас­пределением температуры (смотрите рис. 13.Г. 1), пропорционален температурному градиенту в данном месте:

Ф(х) = - kVT(x)

Закон Ньютона—Флика

Здесь к есть теплопроводность в Вт см-1 К-1. Этот тепловой поток приводит к изменению внутренней энергии Еы (Дж см-3) каждого элемента объема, которое может быть выражено с точки зрения сохранения энергии в следующем виде:

Рис. 13.Г.1. Иллюстрация закона Ньютона—Флика.

Поток

:VT

Т+АТ

^Еш(х, Т)+?Ф(х, Т) = 0 (13.Г.2)

С использованием термодинамики эта внутренняя энергия может быть записана в виде:

Еы = рсрТ (13.Г. Э)

Здесь: р есть удельный вес (г см-3), ас - удельная теплоемкость материала (Дж К-1 г-1).

Если среда обладает внутренними тепловыми источниками, распределенными в соот­

Ветствии с S(x, t) (Вт см-3), то система уравнений (13.Г.1)—(13.Г. Э) приводит к тепловому уравнению Фурье.

= (13. Г. 4)

Э t Эх рс

Тепловое уравнение Фурье

Здесь О есть коэффициент теплопроводности (см2 с-1), определяемый выражением:

0 = — (13.Г.5)

Рср

Коэффициент теплопроводности

Найдем теперь решения уравнения Фурье для двух показательных примеров, кото­рые позволят нам лучше понять тепловые характеристики лазерных диодов.

Эмиссионная поверхность в бесконечной среде: переходная характеристика

Этот пример описывает переходную характеристику лазерного диода в отсутствие теплоотвода. Определим эффективную поверхность теплового источника, включа­ющего все диссипативные механизмы в структуре (омические контакты, поглоще­ние на свободных носителях, безызлучательная рекомбинация и т. д.) после воз­действия токового импульса:

(13.Г.6)

Здесь <?(х) есть 8 — функция Дирака (см1), а #г(0 — ступенчатая функция, равная 1 между 0 и г и нулю в других областях (безразмерный параметр). Для любого момента времени / изменение наклона Т (х) в любом месте эмиссионной поверхно­сти может быть получено интегрированием (13.Г.4) в интервале между — е и +е с учетом того, что Т должно быть непрерывным при х = 0:

[— Лх-о— Ах = ^-Н^)8(х)йх (13.Г.7)

I I Эх2 рср I

Или иначе:

-^-Яг(0 (13.Г.8)

РСР

Здесь мы предположили, что среда симметричная относительно точки х = 0. Это последнее выражение означает, что тепловой поток %Р распределяется равным об­разом по обе стороны перехода. При этом он равен ВдТ/дх.

Для решения (13.Г.4) определим временную функцию преобразования Лапласа:

Й (х, 5>- эТ (х, 5>= ~-^-8{х)

Дх2 рср

Здесь член в квадратных скобках представляет собой преобразование Лапласа сту­пенчатой функции. Однородное решение для левой стороны уравнения имеет вид (для х > 0):

Т Ос, 5>= А («)е-^7Тдг (13.Г.10)

Функция /4(5) может быть получена из условия (13.Г.8) в виде:

1

(13.Г.9)

-51

Это позволяет нам переписать временную зависимость преобразования Лапласа для распределения температуры:

(13.Г.12)

Имеется и обратное преобразование Лапласа для этого последнего выражения, но оно достаточно сложно, как мы увидим это несколько позже. В течение некото­рого времени нас будет интересовать прежде всего нагрев перехода, т. е. ситуация при х = 0. Обратное преобразование Лапласа (13.Г. 12) для х = 0 тривиально и оно определяется выражением:

Т{<)= ^-(Т7-ТГ37) (13.Г.13)

Рсру1пи

Таким образом максимальная температура Ттах достигается в конце токового им­пульса (при t = г), что и неудивительно:

Т - ^ = __ ^_р__________________ (13 г 14)

/тах " Рср4Ш 47Рср10

Записав (13.Г. 14), мы ввели энергию светового импульса Ер = Рт и длину тепло­проводности Ь0 = (Ог)1/2. В записи с использованием указанных параметров (13.Г. 14) становится понятным: имеющий место нагрев является результатом диссипации количества теплоты £Ер в слое материала толщиной Это уравнение также

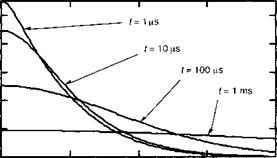
Показывает, что в данной конфигурации диода имеет место постоянный нагрев диода в функции длительности импульса г, что неизбежно приведет к разрушению прибора, если импульс будет достаточно длинным. Таким образом, необходимо искать способы отвода тепла от области перехода. Рисунок 13.Г.2 иллюстрирует полное решение для теплового распределения в функции времени, что дается об­ратным распределением Лапласа (13.Г. 12), а именно:

G 0.8

Аз Q.

^ 0.6 Аз Q.

0

| 0.4

Ш

02

0. 0 ~

0 5 10 15 20 хЮ'3

Расстояние (см)

Рис. 13.Г.2. Зависимость перегрева в ЛД на основе GaAs от расстояния от перехода в различные моменты времени после окончания теплового импульса амп­литуды 200 Вт/см2 длительностью 100 мкс.

Здесь erfc есть дополнительная функция ошибок 1-erf для условий, приведенных в следующем ниже примере.

Пример-----------------------------------------------------------------------------------------------------------------------------------------------------

Используемые физические постоянные для GaAs из таблицы 13.Г. 1 есть:

Р = 5,32 г см-3 ср = 0,35 Дж г-1 К'1 к = 0,46 Вт см"1 К"1 D = 0,25 см2 с'1

В случае диода, рассеивающего количество тепла £/*(Вт см-2) при длительности импульса г (мкс) увеличение температуры составит:

Тт = 6x10 -*£Р(т(мкс ))'л

Пусть лазерная линейка мощностью 100 Вт имеет ширину 1 см и длину 500 мкм. В предположении коэффициента нагрева £ равного 10%, тепловая нагрузка соста­вит = 2 х 102 Вт см-2. Импульс длительностью в 1 мс приведет к увеличению температуры на 3,8 К в то время как после 1 секунды пере фев увеличивается до 120 К, что приводит к необратимому разрушению лазерного диода.

Тепловое рассеяние с двух сторон перехода при непрерывном функционировании

Для предотвращения теплового перегрева с двух сторон перехода должны разме­щаться теплоотводы, например, в точках х = +Ь и х = —Ь. Тепловое уравнение

(13.Г.4), описывающее тепловую характеристику прибора, остается тем же са­мым за исключением того, что теперь используются другие граничные условия (Т(Ь, 0 = Т(~Ь, /) = 0 для любого момента времени /)• В предположении, что

Такая система обладает стационарным решением, стационарное уравнение Фу­

Рье для Т может быть записано в виде:

_|7' (13.Г.16)

Дх К

Благодаря первому интегралу в (13.Г.8) это последнее уравнение может быть проинтегрировано без особых трудностей, что дает Т(х) = (%Р/2к)(Ь — х) для л: > 0. Стационарное падение температуры между источником и теплоотводом, таким об­разом, является линейной функцией. При этом повышение температуры перехода по отношению к теплоотводу составляет:

Л?™ =4^ (13.Г.17)

Это соотношение может быть интерпретировано как способность теплоотвода от­водить мощность %Р/2 на расстоянии Ь с учетом теплопроводности материала к.

В общем случае (13.Г. 17) может быть записано в виде:

ЛТтак=Я^Р (13.Г.18)

Здесь есть тепловое сопротивление системы (см2 К-1 Вт-1).

В случае теплоотвода, расположенного на расстоянии Ь от перехода (смотрите рис. 13.Г. З), тепловое сопротивление дается (13.Г. 18) и составляет:

*Ь=- (13.Г.19)

К

Тепловое сопротивление для теплоотвода, расположенного на расстоянии /. от перехода (см2 К-1 Вт-1)

Пример---------------------------------------------------------------------------------------------------------------

В продолжение предыдущего примера рассчитаем стационарное возрастание темпе­ратуры для того же самого перехода, но на этот раз в присутствии теплоотвода, рас­положенного на расстоянии 5 мкм от перехода. Тепловое сопротивление в рассмат­риваемом случае составляет 5 х 10~4 см/0,46 Вт см-1 К-1 или 1,1 х 10~3 см2 К'1 Вт-1.

Соответствующее возрастание температуры Л7"тах равно 2 х 102 Вт см-2 х 1,1 х 10~3 см2 К-1 Вт-1 или 0,22 К. Сравнение этой величины с полученным ранее значением 3,8 К дает представление о преимуществах использования теплоотводов.

Помимо опасности расплавления лазерного диода существует еще целый ряд других неблагоприятных следствий, связанных с неконтролируемым увеличением температуры перехода. Во-первых, с учетом теплового расширения полупроводни­ков их ширина запрещенной зоны уменьшается с увеличением температуры, при этом длина волны излучения смещается в длинноволновую область спектра. Для типичного лазерного диода на основе СаАз/АЮаАБ скорость температурного сме­щения длины волны излучения составляет приблизительно 3,2 Е К-1. Это может оказать самое негативное влияние в тех областях применения, когда лазерные дио­ды используются для накачки лазерного материала; в этом случае длинноволновый сдвиг приводит к ослаблению перекрытия между спектром излучения лазерного диода и поперечным оптическим сечением ионов (смотрите дополнение 4.Д).

Другим эффектом, связанным с увеличением температуры, является увеличе­ние полного порогового тока /1Ьге5Ьо1(Г Физические механизмы этого многочисленны (эффект Оже, тепловая активация механизмов безызлучательной рекомбинации). Зависимость /1Ьге5Ьо1с1 от температуры прибора может быть промоделирована с ис­пользованием феноменологического соотношения:

/, ы-к*. =/„ег/г” (13.Г.20)

Здесь феноменологический параметр Т0 называется характеристической темпера­турой лазера. Простым правилом, связанным с этим параметром является то, что, чем больше ширина запрещенной зоны и чем глубже квантовые ямы, тем будет выше соответствующая характеристическая температура Т0 и тем более стабиль­ным относительно изменений температуры будет прибор. В таблице 13.Г.2 приве­дены типичные значения Т0, полученные для различных полупроводниковых си­стем. Лазерные диоды, изготовленные на основе гетероструктур СаАз/АЮаАз об­ладают характеристическим температурами порядка 100 К тогда, как лазеры среднего И К-диапазона на основе 1пСа8Ь/1пА8 обладают величиной Т0 порядка 30 К, означая, что эти приборы способны функционировать лишь при низких температурах.

На рисунке 13.Г.4 представлены максимальные рабочие температуры лазерных диодов с длиной волны излучения в диапазоне от 1,5 до 5,5 мкм.

Е

Т

100

■

□

Д

Л . . 1.Л.А............................. , ■ I .... I.... I. . и, I ■ !■■... м||

1.5 2 2.5 3 3.5 4 4.5 5 5.5

Длина волны (мкм)

Рис. 13.Г.4. Максимальные рабочие температуры для полупроводниковых лазеров,

Излучающих в диапазоне от 1,5 до 5,5 мкм: квантово-размерные струк­туры типа I на основе соединений III—V 8Ь, квантово-размерные гете­роструктуры типа II и III на основе соединений III—V 8Ь, солей свин­ца, Н§Сс1Те, а также квантово-каскадные лазеры (частное сообщение А. ЛошШе).