Тепловидение
Уравнение (2.91) дает точное выражение для спектрального распределения излучения черного тела при температуре Т. Тем не менее, нам еще необходимо определить мощность падающего оптического излучения на единицу площади и единицу длины волны, называемую спектральной излунательной способностью (т. е. измеряемую величину, лежащую в основе термографии или теплового отображения).
Рассмотрим элемент поверхности dS резонатора в пределах черного тела (рис. 2.Б.1). В телесном углу dП, опирающемся на этот элемент поверхности, мощность оптического излучения dК, падающего на dS в спектральном интервале dvв течение времени d/, определяется произведением плотности мод р(у) и объема, занимаемого модами (с/2 d0 собО) dП/2p или:
2 2п
Рис. 2.Б.1. Поток теплового электромагнитного излучения черного тела.
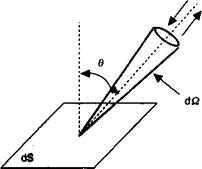 В последнем уравнении коэффициент 2 в с/2 появляется в следствие того, что уравнение (2.91) учитывает стоячие волны (включая как падающие, так и отраженные) тогда как для данного рассмотрения нам нужны лишь волны, падающие на dS. Коэффициент д£1/2к предполагает, что излучение изотропно, а множитель cos 0 учитывает проекцию падающего потока на элемент поверхности dS. Вспоминая, что элемент телесного угла дается соотношением сЮ = 7к sin 0 d0, мы можем проинтегрировать уравнение (2.91) и найти:
В последнем уравнении коэффициент 2 в с/2 появляется в следствие того, что уравнение (2.91) учитывает стоячие волны (включая как падающие, так и отраженные) тогда как для данного рассмотрения нам нужны лишь волны, падающие на dS. Коэффициент д£1/2к предполагает, что излучение изотропно, а множитель cos 0 учитывает проекцию падающего потока на элемент поверхности dS. Вспоминая, что элемент телесного угла дается соотношением сЮ = 7к sin 0 d0, мы можем проинтегрировать уравнение (2.91) и найти:
![]()
|
Cos в sin в 2л |
![]()
|
О |
![]()
|
(2.Б.2) |
![]() De = ~p(y)rfydS
De = ~p(y)rfydS
Спектральная излучательная способность черного тела может быть получена подстановкой (2.91) в (2.Б.2), что дает:
2
|
DR(v, 7’) = |
![]()
|
(2.Б. З) |
![]() Nh y3dy
Nh y3dy
Q 2 Qhv/kT __ J
Наиболее широко используемой формой записи спектральной излучательной способности является ее выражение не через частоту, а через длину волны. С этой целью заменим в (2.Б. З) у на с/Л, что дает:
|
|
(2.Б.4)
Спектральная излучательная способность в Вт м'1 м~г
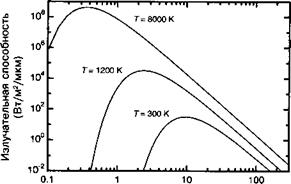
Различные спектры излучения черного тела представлены на рис. 2. Б.2.
При рассмотрении относительной энергии, связанной с фотоном длины волны Л (Не/Л), а также тепловой энергии кТисточника представляют физический интерес два предельных случая:
1. Коротковолновые фотоны с энергией, намного превышающей тепловую энергию источника кТ.
В этом случае уравнение (2.Б.4) приобретает вид:
(2.Б.5)
|
|
Это соотношение действительно для ЛТ< 5000 мкм К и соответствует режиму квантования энергии фотонов, о чем свидетельствует наличие члена ку/кТв уравнении.
2. Длинноволновые фотоны, переносящие энергию, пренебрежимую по сравнению с тепловой кТ: кс/Л « кТ.
Член первого порядка в разложении уравнения (2.Б.4) сразу дает:
4тЯ(Л, Т)= 2ткТЯ-4 аЛ
|
Длина волны (мкм) Рис. 2.Б.2. Спектральная излучательная способность черного тела (Вт м~2 мкм-1) при различных температурах (окружающей, 300 К; «раскаленное железо», 1200 К; поверхность солнца, 8000 К). |
Отметим исчезновение постоянной Планка к в выражении для спектральной излучательной способности. В этом режиме, называемом режимом Рэлея—Джинса, квантовый аспект фотонов маскируется тепловыми возбуждениями системы. Это выражение могло бы быть получено прямо (как это и было сделано Рэлеем и Джинсом), исходя из классического выражения (2.24) для электромагнитной энергии в резонаторе. Отметим также, что (2.Б.6) расходится при Л —> 0, что в начале двадцатого столетия получило образное название ультрафиолетовой катастрофы. Именно эта неудача классической физики привела в конце концов к развитию теории квантов.
Интегрирование (2.Б.4) по всему пространству длин волн приводит к выражению для полной излучательной способности черного тела:
Л(А, Т)= 2пЫ'(2.Б.7)
0
Использование интеграла Бернулли
Де" -1 )Ли = я4 /15
О
Применительно к (2.Б.7) сразу дает:
Я(Л, Т) = аТ4 (2.Б.8я)
Закон Стефана—Больцмана для излучения черного тела
Где а — постоянная Стефана:
С = т^-Дт = 5,67х10~8Вт м~2 К-4 (2.Б.86)
15 сп
Пример--------------------------------------------------------------------------------------------------------------------------------------------------
Рассчитаем полную мощность Р излучения человеческого тела с площадью поверхности 5 = 2 м при температуре 300 К.
Эта величина дает ожидаемые потери энергии незащищенного тела в условиях окружающей температуры 0 К, что встречается отнюдь не так часто!
Как можно увидеть из рис. 2.Б.2, спектры излучения черного тела имеют максимум при определенной длине волны для заданной температуры. Положение это-
|
|
Го максимума может быть определено дифференцированием по Л уравнения (2.Б.4), что дает следующее точное уравнение:
5
|
(2.Б.9) (2.Б.10) Закон Вина |
 ЕАс/ХкТ _ ___ _________________
ЕАс/ХкТ _ ___ _________________
5 - (Ас / ХкТ)
Допускающее в качестве решения следующую зависимость:
. 2898 Л™ =-=-,вмкм
Таким образом, максимум излучения для тела при комнатной температуре располагается на длине волны, примерно составляющей 2898/290 или 10 мкм. Следовательно, тепловое отображение объекта при комнатной температуре возможно при использовании детекторов, чувствительных к излучению на длинах волн в окрестности 10 мкм.
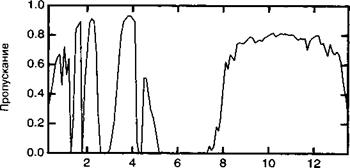
Этот спектральный диапазон представляет интерес еще и потому, что земная атмосфера обладает большой прозрачностью на этих длинах волн. На рисунке 2.Б. З представлен график зависимости прозрачности атмосферы от длины волны.
Отметим в особенности наличие двух широких зон, расположенных в диапазоне 3—5 мкм (зона II) и 8—12 мкм (зона III), в пределах которых земная атмосфера особенно прозрачна.
У каждого из отмеченных окон прозрачности имеются свои особые области применения. В выборе оптимального варианта для поставленной задачи нам может помочь ряд перечисленных ниже соображений:
• климатические условия: влажные воздушные массы лучше сохраняют прозрачность в зоне II, в то время как рассеивающие облака представляют меньшие трудности при использовании зоны III;
• тепловой контраст: понятно, что большая часть излучения объектов при температуре 300 К сосредоточена в диапазоне 8—12 мкм (12,2 мВт см"2 — смотрите приведенный ниже пример), а не в диапазоне 3—5 мкм (0,6 мВт см“2). Тем не менее, иногда нам надо уметь детектировать тепловой источник с температурой Г на фоне окружающей среды с температурой Тъ. Таким образом, тепловой контраст является физически более уместной величиной, соответствующей нормированному различию мощности излучения объекта и фона в спектральном диапазоне А Л или:
|
Длина волны (нм) Рис. 2.Б. З. Спектральная зависимость пропускания атмосферы в типичных условиях (2 км над уровнем моря, 20°С, влажность 40%). |
|
|
|
2. Б. Тепловидение |
|
С(ал)= |
|
Йя + ТМЕЇЇІая А іл |
|
1 |
|
Сі К(Л, Г,) 6Я |
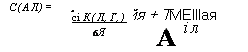 |
|
|
|
|
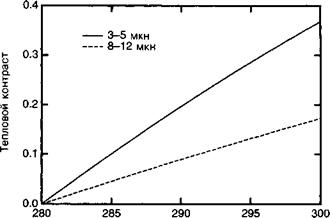
Рис. 2.Б.4 иллюстрирует сравнение теплового контраста в зонах II и III по отношению к фоновой температуре 280 К. Видно, что наибольший контраст достигается в диапазоне 3—5 мкм, что является важным аспектом в зависимости от области применения.
|
Температура мишени (К)
Рис. 2.Б.4. Тепловой контраст в диапазоне 3—5 мкм (зона II) и 8 — 12 мкм (зона III).
Отметим, что хотя число фотонов меньше в зоне II, тем не менее тепловой контраст (или способность различать цель с температурой Т на фоне среды с температурой 280 К) вдвое больше.
Другим важным параметром является дифференциальный контраст С, (Вт см-2 К-1). По определению, С, А Г есть тепловая излучательная способность на градус К в интервале длин волн АА:
|
М&т.) ЙЛ |
|
С. М-и Дя |
|
6Я |
|
|
Этот параметр чрезвычайно полезен при предсказании функциональных характеристик инфракрасных детекторов. Если обозначить чувствительность детектора с площадью 5 как 57 (А/Вт), то ток детектирования / (А) вследствие вариации температуры АТ дается соотношением:
|
(2.Б.13) |
![]() /= 55/С/(АД)А Т
/= 55/С/(АД)А Т
Пример-------------------------------------------------------------------------------------------------------------
Программа МАТЕМАТІСА, приведенная ниже, позволяет рассчитывать излучатель - ную способность абсолютно черного тела в спектральном диапазоне А— Л2, а также дифференциальный контраст.
С=2.98810”8(*т/з*); к=1.3810’-23(*и/К*);
|
|
H=6.62510’-34(*J. s*); hb=h/(2*3.1416); m0=0.9110’-30(*kg*);
(* Wavelength range in mm *) iambda1= 8;lambda2= 12;
(* Blackbody as a function of temperature*) temp=.; Iambda=.; emm:=2*3.1416*h*c’2*(lambda*10’-6)’-5/(Exp[hV((lambda*10’- 6)*k*temp)]-1) emm = emm * 1(Г-6 (* W/nT2/|im*); contr=D[emm, temp];(*contrast used for the calculation of NETD*) temp=300 (temperature of the blackbody*);
Plot[emm,{lambda,. 1,20}, Frame - >True, RotateLabel - > False, FrameLabel - > {«micron’Y’W/m''»} ]
Plot[contr,{lambda,.1,20}, Frame - >True, RotateLabel - > False, FrameLabel - > {«micron’Y’W/mVK»} ]
(* Blackbody power radiated over the spectral range*)
Nlntegrate[emm,{lambda, Iambda1,lambda2}] (*W/nT2*); pp=%*10’-4(*W/cm’2*)
(* differential contrast for the spectral range *)
Nlntegrate[contr,{lambda, lambda 1 ,lambda2}] (*W/m’2/K*); cc=%*1 (r-4(*W/cm’2/K*)
Эта программа дает для источника с температурой 300 К плотность мощности излучения в спектральном диапазоне 8—12 мкм и 3—5 мкм соответственно 12,2 мВт см"2 и 0,6 мВт см-2. Таким образом, сигнал детектора будет существенно больше в зоне Ш по сравнению с зоной II. С помощью программы мы определяем также дифференциальный контраст в диапазонах 3—5 мкм и 8—12 мкм, составляющий соответственно 2,1 х 10~5 Вт см-2 Кг1 и 1,98 10~4 Вт см-2 К-1. При использовании детектора с площадью 10 см2 и чувствительностью 1 А/Вт вариация температуры источника величиной 10 мК приведет к току датектирования величиной 20 и 200 пА соответственно в диапазонах 3—5 мкм и 8—12 мкм. Такой уровень тока является достаточно надежно измеряемым, что свидетельствует о практической важности инфракрасных детекторов. Вновь к этим важным приборам мы возвратимся в главе 11.
В заключение следует подчеркнуть, что большинство обычных объектов в действительности не являются черными телами. Они поглощают только часть излучения Л), при этом остающаяся часть излучения либо отражается, либо переносится. Таким образом, спектральная излучательная способность dR/йЛ связана с аналогичным параметром абсолютно черного тела dRBB /йЛ соотношением:
±Я(Л, Т)= еЛЛ^ЛЛ, т) (2.Б.14)
Типичные значения поглощательной способности варьируются в диапазоне от
0, 03 для полированного алюминия (который считается хорошим отражателем) до
0, 95 в случае черной сажи (хороший поглотитель)