Спонтанное излучение И излучательное время жизни. Спонтанное излучение
В том случае, когда второй уровень заселен, он стремится срелаксировать под воздействием потока фотонов, о чем свидетельствует член —&ор(?пЫ2/У в (3.49). Таким образом, если число фотонов в резонаторе равно нулю (т. е. в резонаторе отсутствует излучение) скорость стимулированного излучения также равна нулю. В результате этого в отсутствие упругих соударений (Г, = 0) частица должна оставаться в возбужденном состоянии сколь угодно долго. Это, однако, противоречит опыту. Например, когда атомы возбуждаются электрическим разрядом в разряженной атмосфере для того, чтобы свести к минимуму атомные столкновения (как это специально делается в неоновых лампах), возбужденные атомы релаксируют в течение нескольких микросекунд. Каким же образом можно примирить этот парадокс между до сих пор безупречной теорией и этим бытовым наблюдением из области каждодневной практики?
Ответ же заключается в том, что мы выполнили только половину задачи. В то время, как мы допустили квантование поведения частицы, мы не сделали то же самое в отношении света. Для завершения нашей работы мы должны ввести в выражение для гамильтониана взаимодействия (3.12) и (3.13) квантовую форму электрического поля, соответствующего моде /, которая дается уравнением (3.34л):
|
(3.57) |
![]() W =qFl(aIt'kT-a*ls )£,*?
W =qFl(aIt'kT-a*ls )£,*?
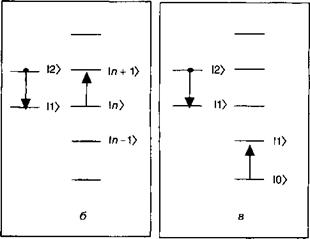
Где а1 и а* операторы рождения и уничтожения фотонов моды /, а /) — интенсивность поля, связанного с квантовыми вакуумными флуктуациями той же самой моды (уравнение (2.35)). В этом случае гамильтониан действует в двух гильбертовых пространствах (или более точно воздействует на тензорное произведение), соответствующих пространству фотонов и заряженных частиц. Таким образом, в этом случае мы должны говорить о состояниях, обозначаемых как |/, п), где / относится к состоянию заряженной частицы (/=1,2 для двухуровневой системы), а п{ обозначает число фотонов моды / (смотрите рис. 3.3). Обобщение этой задачи на случай произвольного числа мод следует прямо, но сопровождается усложнением необходимых обозначений (например |/, ..., пп...». В связи с этим на время мы оставим
В стороне модовые индексы.
Оптические переходы могут иметь между состояниями 11, п) и |2, я'), а также в обратной последовательности. Рассмотрим сейчас механизм поглощения. В этом случае начальным уровнем является |1, л), а конечным — 12, п — 1) (смотрите рис. 3.3), так как фотон в процессе поглощения теряется. Из (1.856) следует, что вероятность поглощения составляет:
|
|
(3.58)
Где Ein = Е{ + h со(п - I - 1/2) и ЕГт = Е2 - I - Ь со((п — 1) + 1/2). Закон сохранения энергии в данном случае соответствует условию h со = Ех — Ev что находится в согласии с теорией главы 1 (уравнение (1.80)). В таком случае уравнение (3.58) может быть записано в виде:
|
|
Поскольку состояние частицы и фотона не зависят друг от друга, это выражение может быть разделено следующим образом:
|
|
|
12) 1/7+1) 11) ------- г 1п> 1л-1> |
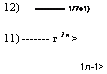
|
I |
![]()
|
Т |
![]() Рис. 3.3. Взаимодействие между двухуровневой системой и квантованным электромагнитным полем в виде гармонического осциллятора. Рисунок показывает различные механизмы для следующих оптических переходов: а — поглощение;
Рис. 3.3. Взаимодействие между двухуровневой системой и квантованным электромагнитным полем в виде гармонического осциллятора. Рисунок показывает различные механизмы для следующих оптических переходов: а — поглощение;
Б — стимулированное, или индуцированное излучение, в — спонтанное излучение.
С учетом свойств операторов рождения и уничтожения ((1.Г.23) и (1.Г.24)) можно установить, что единственным ненулевым членом, связанным с фотоном, является:
(п - 11*2/1«) = уГп (3.61)
В этом случае вероятность поглощения в единицу времени приобретает вид:
Р>.2 = “Щ I (% • г|2) |2 8{Па> =Е2- £,) (3.62)
Или вновь используя выражение (2.77) для электрического поля в когерентном состоянии: />аЬ! = ± Е? 1(1 це, ■ г12) |2 б{Пт = £,-£,) (3.63)
Таким образом, мы точно воспроизвели выражение (1.856) для классического электрического поля (испытав удовлетворение от полного согласия между теориями).
Теперь рассмотрим резонатор, содержащий п фотонов в моде /, но на этот раз также и частицу, находящуюся изначально в состоянии |2). Излучение в этом случае соответствует переходу из состояния |2, п) в состояние |1, п) (рис. 3.3). В этом случае вероятность перехода имеет вид:
Кг =у?2^2|(« + 1|(^г -<е-*'г)|л)|2 I (1е, ■ г 12) I2 8{Пю=Ех-Ег) (3.64) При этом единственным ненулевым членом, связанным с фотонами, является:
(п +1 а+1 п) = л/я + 1 (3.65)
И вероятность эмиссии в единицу времени приобретает вид:
= 77т (« +1 }(* я£! р12)|2 8(Ц ю = Е2 - Е,) (3.66)
£0Ь
Приведенное выше выражение показывает, что в излучении проявляются два различных эффекта:
1. Механизм излучения, при котором скорость перехода пропорциональна числу фотонов, уже присутствующих в резонаторе — это явление стимулированного излучения, рассмотренное ранее.
2. Новый механизм излучения, проявляющийся даже тогда, когда в резонаторе нет фотонов — называется спонтанным излучением. Скорость спонтанного излучения дается выражением:
|
(3.67) |
![]() С. =^тН(1 & г|2) |2 б(Нсо = £,-£,)
С. =^тН(1 & г|2) |2 б(Нсо = £,-£,)
Є0Ь
Мы можем интерпретировать этот член как член, соответствующий скорости эмиссии, стимулированной вакуумными флуктуациями Гг Под влиянием вакуумных флуктуаций частица может срелаксировать, освобождая фотон в моду п. Очевидно, что частица может излучить этот фотон в любую из возможных резонаторных мод. Полная скорость спонтанного излучения получается суммированием всех вкладов
(3.67) для различных мод с частотой соп:
|
|
(3.68)
![]() Расчет этого интеграла использует выражение (2.83) для плотности электромагнитных мод в резонаторе и не представляет особых трудностей, так как мы можем расширить область интегрирования по всему пространству, как это было оценено в (2.А.25). Таким образом, мы получаем скорость спонтанного излучения по всем пространственным направлениям для квантового перехода с энергией Н со0 в оптической среде с коэффициентом преломления пор:
Расчет этого интеграла использует выражение (2.83) для плотности электромагнитных мод в резонаторе и не представляет особых трудностей, так как мы можем расширить область интегрирования по всему пространству, как это было оценено в (2.А.25). Таким образом, мы получаем скорость спонтанного излучения по всем пространственным направлениям для квантового перехода с энергией Н со0 в оптической среде с коэффициентом преломления пор:
(3.69а)
Скорость спонтанного излучения и излучатель - ное время жизни для двухуровневой системы
Где:
|
(3.696) |
Напоминаем, что это выражение действительно только в том случае, когда фотоны излучаются изотропно.
Следует отметить несколько моментов:
1. Если частица находится на своем основном уровне |1), скорость спонтанного перехода равна нулю, т. е. время жизни электрона на основном уровне бесконечно. Таким образом мы разрешаем одну из величайших головоломок теоретиков в начале столетия, а именно выясняем причину, почему все электроны на всех атомных орбитах во вселенной просто не разрушаются на своих ядрах в течение наносекунд, излучая при этом фотоны.
2. Степенная зависимость (со3) скорости спонтанной эмиссии предсказана классической теорией Рэлея. Предполагая постоянным дипольный элемент, находим, что время жизни спонтанной эмиссии становится меньше по мере возрастания энергии перехода. Это является одной из причин, почему рентгеновские лазеры труднее создать, чем инфракрасные лазеры. Безусловно, дипольный матричный элемент также будет зависеть от энергии перехода, как это будет проиллюстрировано примером, приведенным ниже.
3. Отсутствие постоянной Планка % в уравнении (3.67) показывает, почему классический подход, использованный в Дополнении 2.А мог бы быть успешно применен в некоторых случаях.
Пример: излучательное время жизни в бесконечной квантовой яме---------------------------------------------
Рассмотрим квантовую яму на основе ваАв шириной а с бесконечными барьерами, в которой:
Т = 0,067л770 п = 3,3
Ор 7
Мы видели в главе 1, что энергетический зазор Ь со21 между уровнями и диполь - ный матричный элемент zn даются соотношениями:
|
- Е - Е - ^ ^ 71 2 1 2 та2 |
|
Ьсо-у |
|
Г'2 з2 ~2 |
|
А Л2 |
|
|
Таким образом, мы получаем выражение для излучательного времени жизни в функции энергии перехода:
|
|
||
|
|
||
|
|
||
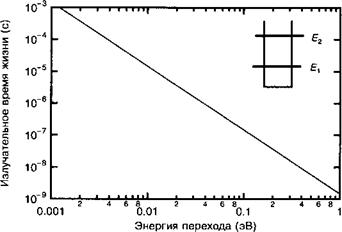
Зависимость времени жизни от энергии перехода в рамках простой модели представлена на рис. 3.4. Для типичных значений энергии перехода, лежащих в диапазоне от 50 до 250 мэВ, соответствующие времена жизни лежат в диапазоне от 10 не до 1 мкс. Мы видим, что излучательное время жизни в этом случае пропорционально со~2, а не со~3 (как это показано выше), и является результатом зависимости дипольного матричного элемента гп от энергии перехода.
|
Рис. 3.4. Излучательное время жизни в функции энергии перехода между двумя уровнями в квантовой яме ваАз с конечными барьерами |
Приведенный выше пример иллюстрирует возможности классического подхода к описанию спонтанной эмиссии. По этой причине мы вводим отношение классического излучательного времени жизни /с1а5, которое дается (2.А.30) и квантового времени жизни t :
2тг> (3.716)
Теперь все квантовые структуры (ионы, атомы, полупроводниковые квантовые ямы...) могут быть в первом приближении описаны моделью бесконечной квантовой ямы шириной а с энергией перехода Н со и дипольным элементом г12, определяемой соотношением:
|
|
|
|
И гп = аа,
Где ТУ — целое число в диапазоне от 1 до 10, а а — действительное число порядка 10~‘. Следовательно, отношение *с1а8/* , таким образом, может быть записано в виде:
^- = а^2л2 =1
БрОП
Классическое выражение для излучательного времени жизни имеет, таким образом, смысл, но с его помощью не удается описать такие эффекты, как стабильность основного состояния квантовых структур, переходы, запрещенные правилами симметрии и т. д.