Скоростные уравнения с учетом спонтанного излучения
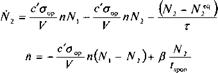Теперь мы включим спонтанную эмиссию в скоростные уравнения в (3.49) и (3.50). Для временного упрощения необходимых обозначений предположим до явного упоминания, что в резонаторе существует лишь одна мода. Спонтанную эмиссию и время жизни на уровне Г, будем учитывать введением членов ±Л^2//роп ±Ы1/Т1 и ±N2/Tl в скоростные уравнения для электронов (3.49). В том, что касается (3.50) только доля Р спонтанно излученных фотонов будет переходить в резонаторную моду. Соответственно, мы добавляем член рЫ2 //5роп в скоростное уравнение для фотонов (3.50), что дает:
|
|
(3.72а)
Скоростные уравнения для резонатора
Где 7 — время жизни в состоянии |2), что с учетом спонтанного излучения принимает вид:
|
|
Называется коэффициентом спонтанной эмиссии. Введение членов в (3.72а) гарантирует, что система возвращается в состояние термодинамического равновесия, как только прекращается возбуждение.
Теперь нам остается только связать выражение для излучательного времени жизни с оптическим поперечным сечением, что окажет нам помощь в ряде предстоящих рассмотрений. В предположении, что спонтанное излучение изотропно (хп —уп = 1п), (3.46) и
(3.69) приводят нас к следующим известным уравнениям:
|
|
(3.73)
|
И |
Оптическое поперечное сечение и излучательное время жизни
|
(3.74) |
|
А(у)= -------- -2------- 1(у - у21 )(ЛГ, - ЛГ2) |
Коэффициент поглощения и излучательное время жизни
Где Л — вакуумная длина волны, а как мы напоминаем, — функция Лоренца.Полихроматические переходы
Уравнение (3.63) дает нам вероятность поглощения для электромагнитной волны в двухуровневой системе. Это уравнение может быть легко получено в рамках нестационарной теории возмущений так же, как в рамках теории квантования электромагнитного поля. Замена функции Дирака на функцию Лоренца возвращает нас обратно к соотношению
(3.37) , полученному с использованием формализма матрицы плотности. Другое использование (3.63) относится к случаю, когда переход происходит вследствие произвольного распределения энергии ре(у). Эта ситуация имеет особе значение в твердых телах, где оптические переходы происходят между энергетическими зонами.
Таким образом, рассмотрим объем V, в котором спектральное распределение энергии ре(у) определено (предполагается, что ширина распределения больше, чем в случае изолированных атомных переходов). В диапазоне от у ло у + йу имеется ре(у)Уйу/Иу фотонов (где ре выражено в единицах энергии на единицу частоты и единицу объема). Каждый фотон характеризуется вероятностью оорс/Упор (смотрите (3.49)) индуцировать переход (либо за счет поглощения, либо за счет стимулированного излучения). В этом случае полные скорости поглощения и стимулированного излучения составляют:
|
|
|
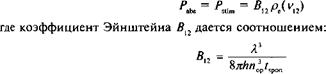(3.76)
(3.77 а)
Коэффициент Эйнштейна для поглощения и стимулированного излучения
Другим коэффициентом, введенным Эйнштейном, является скорость спонтанного излучения:
|
|
Теперь скоростные уравнения могут быть обобщены с тем, чтобы описывать полихроматические переходы между зонами шириной йу:
|
(3.78) |
С!#, = - с1#2 = Л12с1ЛГ2 + (с1ЛГ2
Скоростное уравнение Эйнштейна
Где и теперь обозначают дифференциальные величины = рх(у) и йИ2 = рх(у) йу и где р.5 соответствует плотности заселенности на единичный частот
Ный диапазон переходов (в с см-3). В распоряжении Эйнштейна не было концепции квантованного электромагнитного поля, с помощью которого можно было бы установить соотношение (3.78). Скорее он действовал эвристически, исходя из скоростных уравнений (3.49), которые позволили ему получить распределение Планка для ре{у) при тепловом равновесии. Этот подход более детально исследован в дополнении З. В.
