Синусоидальное возмущение
В рассматриваемом случае потенциал возмущения может быть записан в виде:
|
(1.75) |
![]() W (г,/) = W (г, 0 sin cot
W (г,/) = W (г, 0 sin cot
![]() Уравнение (1.74) сразу приводит к нестационарной вероятности перехода /^(0 между начальным и конечным состояниями:
Уравнение (1.74) сразу приводит к нестационарной вероятности перехода /^(0 между начальным и конечным состояниями:
(1.76)
В данном случае мы выполняем процедуру, которая классически называется аппроксимацией фазы вращения или квазирезонанса, при которой пренебрегается вклад члена с большим знаменателем сол + со по сравнению с членом, имеющим меньший знаменатель сол — со. Таким образом, сохраняя второй член в выражении
(1.76) ![]()
|
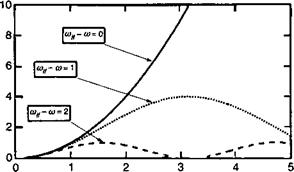
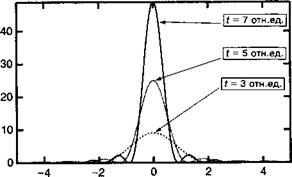
Рисунок 1.4 иллюстрирует эволюцию этой вероятности в функции времени для различных частот (или отстройки) между возбуждающим полем и резонансной частотой перехода со — сол. Отметим, что по мере того, как частота возмущающего поля приближается к боровской частоте колебаний (т. е. со -> со/?), временная зависимость амплитуды перехода изменяет свой характер: от синусоидальной к параболической зависимости от t. Дополнительно на рис. 1.5 показано спектральное распределение вероятности перехода в функции отстройки для различных значений времени /. Эта функция представляет собой произведение синусоиды на временную параболу, которая стремится к 8 — функции Дирака при / —> «>. Таким образом перепишем (1.77) в виде: |

|
(1.78) |
![]()
|
Где sin с (х) есть sin х/х. Уравнение (1. 78) при внешней простоте трудно охватить сразу во всей его полноте, так как оно является функцией двух внутренне связанных величин, а именно времени и частоты. Для лучшего понимания его характера рассмотрим три различных случая. |
![]() Мы приходим к выражению:
Мы приходим к выражению:
|
N2 |
1 _ |
2 _ КГ |
/ |
'{(0Л-0)) |
|
|
4 h2 |
Со п - со |
1 |
1 <N 3 1 |
/ |
1 Ю 1 |
|
T(^/((Dif-(o)) Рис. 1.4. Временная эволюция вероятности перехода между уровнями / и /для различных величин частотной отстройки со^ — со. В условиях вне резонанса электроны осциллируют между двумя уровнями. |
|
(сом - я;)( 1/огЬ • ипК) Рис. 1.5. Вероятность перехода между двумя уровнями / и / в функции частоты отстройки для различных моментов времени наблюдения / (в произвольных единицах). При большем значении времени возможны лишь переходы между состояниями, удовлетворяющие требованиям сохранения энергии. Это согласуется со вторым принципом неопределенности Гейзенберга. |
Случай 1: переходы между дискретными уровнями,
Обусловленные одночастотным возбуждением
В этом случае в процессе доминирует резонансный переход, при этом:
{2 (1-79)
Поскольку вероятность указанного перехода возрастает квадратично со временем, предлагаемое описание носит аппроксимационный характер, так как параметр не может превысить единицу. В дополнении 1. Д мы увидим, что эта апрокси - мация действительна только для очень коротких промежутков времени, в течение которых разложение нулевого порядка (1.69) может считаться действительным. Отметим, что резонансное условие со= со л альтернативно может записано в виде:
|
(1.80) |
![]()
|
Ьсо = Е/ - Е, = Ьсоп |
![]() Боровская частота
Боровская частота
Это уравнение описывает закон сохранения энергии с учетом энергии, переданной системе, и различием энергии системы между начальным и конечным состояниями АЕ = Ег — Ег С технической точки зрения, касающейся расчета этих величин, отметим только, что упорядочение в расположении индексов в этих уравнениях ({IV = |И^|) не играет какой-либо определенной роли из-за свойств эрмитовых произведений. В то же время сказанное не относится к боровской частоте колебаний (о^— —а>г
В дополнение к сказанному, рис. 1.5. иллюстрирует тот факт, что вероятность перехода становится пренебрежимо малой, как только
(1.81)
Это последнее условие известно также и как второе соотношение неопределенности Гейзенберга. Оно обеспечивает возможность снятия ограничений на сохранение энергии при возбуждении, действующем в течение коротких периодов времени.
Случай 2: переходы между дискретным уровнем и континуумом, обусловленные одночастотным возбуждением
В этом случае конечные состояния образуют континуум, описываемый непрерывной переменной а)р и вероятность перехода между дискретным уровнем и континуумом Р. с (/) рассчитывается суммированием вероятностей по плотности конечных состояний р(сог):
+©о Г П
|
(1.82) |
![]() ^(0=-^7/2||И//(%)|2 йп с {-°г' 2 р(соіі)й(0/і
^(0=-^7/2||И//(%)|2 йп с {-°г' 2 р(соіі)й(0/і
Теория распределений показывает, что если функция | 2р(сол) обладает нор
![]() Мальным характером (т. е. способностью нормировки и слабой скоростью изменения), то:
Мальным характером (т. е. способностью нормировки и слабой скоростью изменения), то:
(1.83)
Где 8 — есть ^-функция Дирака. Таким образом при больших значениях времени уравнение (1.82) принимает вид:
|
|
(1.84)
Приведенное выше уравнение свидетельствует о том, что, если переход происходит из дискретного состояния в континуум, то скорость перехода <7, = йР. с/& является постоянной по времени и имеет величину, задаваемую соотношением:
|
|
(1.85а)
Частотное выражение золотого правила Ферми
Или
|
|
(1.856)
Энергетическое выражение золотого правила Ферми
Это важное уравнение называется золотым правилом Ферми. Оно утверждает, что в условиях монохроматического возбуждения со только уровни континуума с энергией ЕЛ Нсо будут заселенными под воздействием оптического возбуждения, при этом скорость оптических переходов будет даваться приведенным выше уравнением.
Случай 3: переходы между двумя дискретными уровнями при многочастотном возбуждении
В этом случае используется возбуждение, содержащее континуум возбуждающих частот:
G(co)W Г1{со)^т (со()бсо (1.86)
О
Где #(со) — спектр возбуждения и ¥л матричный элемент гамильтониана взаимодействия для каждой конкретной длины волны. Рассуждения, строго соответствующие приведенным выше, дают скорость переходов в соответствии с соотношением:
Скорость переходов при широкополосном возбуждении