Шум фотоприемника
В дополнениях З. А. и 4.Г мы обратились к некоторым аспектам теории шумов для того, чтобы учесть статистические свойства света. Поскольку понятие «отношение сигнал/шум» является основополагающим для детектирования света (и сигнала!), мы в этом разделе продвинем дальше математический формализм теории шумов. Здесь рассматриваются также и физические механизмы, ответственные за генерацию шума в приемниках излучения.
Перед тем, как приступить к достижению основных целей настоящего дополнения, нам хотелось бы рассмотреть достаточно простой (и достаточно далекий от строгости) аргумент, который позволит нам быстро вывести формулу для генерационного шума, что и является целью этого дополнения. Такая схема рассмотрения будет нам полезна как концептуальная путеводная нить до тех пор, пока мы не разработаем более точную теорию.
Рассмотрим поток фотонов Ф, падающий на приемник излучения с квантовой эффективностью г] в течение времени Т (смотрите рисунок 11.А.1). Это характеристическое время есть время интегрирования приемника излучения, которое также составляет 1/2AV, где Аv есть ширина полосы детектирования. В течение этого временного интервала создается N фотоэлектронов. N есть случайное число со средним значением, определяемым N = т]ФТ и, если jY флуктуирует в соответствии с распределением Пуассона, дисперсия этой величины определяется как о2 = N. Ток фотогенерации может быть оценен числом носителей, создаваемых за единицу времени, как / = qN/Т. Ъ этом случае среднее значение и дисперсия фототока даются соотношениями:
А = Iqlдv
* У
|
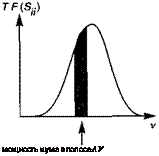
Мощность шума в полосе Ау |
Таким образом, мы получаем формулу (11.А.38), связывающую среднюю величину тока и его дисперсию, Теперь мы проведем указанный вывод более корректно.
Фотоны
Электроны
Рис. 11.А.1. Шум в процессе детектирования (а) и соответствующий спектр шума! фотогенерированном токе (б).
|
|
