Рис. 6.10. Влияние электронного переброса между в — и — долинами при увеличивающейся напряженности поля. Электроны — долины с малой скоростью ответственны за область отрицательного дифференциального сопротивления в зависимости от средней скорости напряженности поля. Рекомбинация
Именно возможность сосуществования одновременно электронов и дырок образует основу для использования полупроводников в оптоэлектронике (и, в значительной степени, электроники как таковой).
В главе 5 мы видели, что при термодинамическом равновесии концентрации электронов п0 и дырок р0 связаны соотношением п0 р0 = п~ (7), где я — собственная концентрация носителей (уравнение (5.49)). Концентрациями п0 и р0 можно управлять легированием. Такое равновесие можно нарушить, создавая электронно-ды - рочные пары, например, освещая образец (оптическая накачка) или инжектируя носители с двух сторон границы раздела областей п - и р-типа проводимости (т. е. рп-переход).
Природа консервативна в том, что она всегда обеспечивает проявление ряда механизмов, способных привести систему обратно в состояние равновесия. В случае электроннодырочных пар такими механизмами являются генерационно-рекомбинационные процессы. Каждый процесс нуждается в соответствующем взаимодействии. Взаимодействие с электромагнитным полем приводит к излучательной рекомбинации, при которой фотон излучается в то время, как поглощение фотона соответствует процессу генерации электронно-дырочных пар. Два указанные процесса являются основным предметом настоящей книги и они будут рассмотрены детально, в особенности, в следующей главе.
Безызлучательные генерационно-рекомбинационные механизмы зачастую являются раздражающим фактором в оптоэлектронике, так как они проявляются параллельно и конкурируют с излучательными процессами. В связи с этим для оценки функциональных возможностей и ограничений оптоэлектронных приборов важно понимать эти процессы. Двумя доминирующими процессами этого рода являются:
1. Рекомбинация Шокли—Рида—Холла, при которой важную роль играют примеси. В этом случае сначала электрон, а потом дырка захватываются той же самой примесью, устраняя тем самым одну электронно-дырочную пару.
2. Оже-рекомбинация, являющаяся результатом электрон-электронного взаимодействия, при котором электрон рекомбинирует с дыркой и передает энергию, выделяющуюся в процессе рекомбинации, другому электрону (или дырке) в виде кинетической энергии. Этот процесс является собственным и не требует участия дефектных или примесных центров. Соответствующим генерационным процессом является ударная ионизация, при которой электрон с достаточной кинетической энергией может создать электронно-дырочную пару за счет передачи своей энергии электрону в валентной зоне, что вызывает его переход в зону проводимости.
Эффект Оже и ударная ионизация рассматриваются в дополнении 6. Г. Здесь же мы опишем рекомбинацию Шокли—Рида—Холла (рис. 6.11).
СВ
—
|
Ловушка |
![]() Рекомбинация
Рекомбинация
Св Шш шш щт
Ловушка — ж генерация
УВ
Рис. 6.11. Рекомбинация Шокли—Рида—Холла и генерационные процессы (СВ-зона проводимости, УВ-валентная зона).
Для детализации картины предположим, что в материале имеются примеси с концентрацией вызывающие существование состояний с энергией ЕТ в запрещенной зоне. В дополнении 5.Г. мы видели, что примесь может создать глубокий электронный уровень (т. е. разрешенное состояние) в запрещенной зоне полупроводника. Дополнительный электрон, предоставляемый донором может быть ионизирован и он переходит в зону проводимости, оставляя положительно заряженный донорный атом в соответствии с реакцией:
N° <-> УУ; + е (6.44)
Ионизированный донор может также захватить электрон из валентной зоны, что соответствует созданию дырки в соответствии с реакцией:
N1 <-> Щ + И (6.45)
В первой реакции число электронов, создаваемых в секунду, пропорционально числу нейтральных ловушек:
Где ее — коэффициент эмиссии (с-1)- Обратный процесс, описывающий рекомбинацию при захвате, пропорционален числу электронов и ионизированных ловушек:
(6.47)
|
(6.48) |
|
G. = R, |
|
N: |
|
Такой тип рассуждений, при котором мы получаем выражение общего характера, связывая излучение и рекомбинацию с использованием частного случая равновесия, полностью аналогичен с ходом рассуждений Эйнштейна, представленным в дополнении З. В (при установлении связи между коэффициентами стимулированного и спонтанного излучения В и А). Уравнение (6.47) называется принципом детального равновесия. В том, что касается второй реакции (6.44), мы подобным образом находим: |
|
|
 |
|
|
|
|
|
|
|
|
|
АГ + 1УТ.. п № _ ПІІ + — О '*о J- Гиу т |
|
= G-R=c |
|
— D7 |
|
|
|
^ = <7* - = с„ Dt С учетом распределения Ферми мы имеем: |
|
NjNc expl —— |
|
-n;h |
|
= с. |
|
KBT |
|
Dt Dр dt |
|
ET-EV K„T |
|
-N? p |
|
N j Nvexp |
|
= с, |
|
Ef-e, KtT |
|
P0 = Nr exp Таким образом, выражения (6.50) и (6.51) приобретают вид: d п |
|
NT _ |
|
- = ехр |
|
N; nt - n; В случае невырожденного полупроводника: |
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
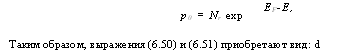 |
|
 |
|
|
|
|
|
Ec - ET kj |
|
+ n |
|
ET-EV K. T |
|
Nc exp |
|
+ P |
|
+ c. |
|
|
|
|
|
|
|
|
|
|
|
ET - Ev kj |
|
ChNv exp |
|
ET - Ev kj |
|
Nc exp |
|
+ c. |
|
+ n |
|
+ P |
|
Ec Ej kBT |
|
+ cn |
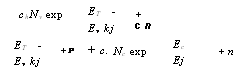 |
|
|
|
|
|
|
|
При этом скорость рекомбинации составляет:
|
D n D7 |
|
1 |
|
P + Nv exp |
|
C. NT |
|
1 |
|
N + Nc exp |
|
C„NT |
|
||
|
||
|
||
|
||
|
Это формула может быть также выражена через время жизни —dя/d/ = (п — л0)/гл: 1 (пр - п - )/{п - »0 )
|
При этом r0 = /cNTu г, = 1 /chNT.
Кажется, что представленное выражение имеет сложный вид. Тем не менее начнем анализ с того, что выражения, зависящие от ЕТ, равны концентрациям электронов и дырок, которые мы бы имели в случае, когда уровень Ферми совпадал бы с Ет. Далее, два важных случая приводят к двум важным пределам:
1. В случае почти собственного полупроводника (п0 « р0 ~ п), когда ловушки располагаются вблизи центра запрещенной зоны и в случае сильной накач - ки Sn = п — п0 = Sp = p ~ pQ » п.:
1 6п2 / фn _ 1
|
= NT C,+Ch |
![]() (6.58)
(6.58)
+ 7,0*» 7„0 + тр0
2. В случае полупроводника р-типа проводимости (п0 = п?/р0 « п.) ловушки располагаются вблизи центра запрещенной зоны и 6п, 6р « р0:
|
(6.59) |
![]()
|
— N ТСе |
![]() Ро
Ро
ТпоРо
В этих двух случаях время жизни не зависит от концентрации, и само понятие «время жизни» теряет смысл.
Пример---------------------------------------------------------------------------------------------------------------------------------------------------
Коэффициент захвата может быть записан в виде где соответствует попе
Речному сечению захвата, а у|Ь есть тепловая скорость у1Ь2 = < у2 >. Для 8 ~ 1015 см"2 и ~ 107 см/с мы имеем с « 10"8 см/с. Коэффициент эмиссии определяется (6.48) и (6.52), при этом:
|
KBT |
![]() Є* = CeNc ехр
Є* = CeNc ехр
При Ис = 5 х 1017 см-3 и в предположении, что дырки располагаются на 0,4 эВ ниже зоны проводимости (кислород в ваЛз) мы имеем ее = 560 с-1 при комнатной температуре.