Резонаторы Фабри—Перо и брэгговские отражатели
Оптическая обратная связь, обеспечиваемая зеркалами, является обязательной для установления лазерных колебаний в оптическом резонаторе. Мы видели, что для того, чтобы в резонаторе установился лазерный режим, должны быть выполнены два условия: одно условие накладывается на усиление (4.21л), а другое — на фазу (4.24). Это последнее условие означало, что лазерные моды должны были быть собственными модами оптического резонатора. Для задания резонатора могут использоваться два типа зеркал — металлические зеркала и диэлектрические зеркала. Диэлектрические зеркала особенно важны в полупроводниковых лазерах, в особенности, в поверхностно-излучающих лазерах с вертикальным резонатором (УСЗЕЬв). Формализм, используемый при описании распространения волны в слоистой среде идентичен тому,
который описывает распространение волны в слоистом волноводе. Таким образом, это дополнение удачно вписывается в главу, посвященную волноводам.
Для начала рассмотрим электромагнитную волну с частотой о)=2жу, распространяющуюся в двух средах (1 и 2) с общей границей раздела при I — 0 (смотрите рис. 9.Г.1). Амплитуды волны в каждой среде определяются действительной частью выражения:
|
І к, і |
![]()
|
(9-Г.1) |
![]() Е&) = £ие^ +Еис
Е&) = £ие^ +Еис
|
П~П2 Пх + п2 |
|
Рп — |
|
Реальные волны, безусловно, имеют вид Ке(£(г)е1<и')- Индекс Я показывает, что амплитуда соответствует волне, движущейся направо (ек<у' ~кд) в то время, как индекс Ь соответствует волне, движущейся налево (ек<у' + ь>). После этого запишем уравнения Френеля, устанавливающие непрерывность электрического и магнитного полей на границах раздела. Поскольку В = к х Е/со (смотрите (2.17а—г)) и к. = 2т./Х^ где Л0 есть длина волны в вакууме, а п. — коэффициент преломления в среде /, эти два условия при I = 0 приобретают вид: |
|
+ Е ц — Е К2 + Е12 КЕ, — к1Е1Х = к2ЕК2 — к2Е12 Предположим, что волна падает слева, т. е., что Еи уравнений (9.Г.2) может быть легко решена, что дает: Е я 2 = ^12^Л1 |
|
Ей —РпЕК |
|
(9.Г.2) 0, при этом система (9.Г. З) |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
-Я1 “И |
![]() Рис. 9.Г.1. Распространение волны через границу раздела.
Рис. 9.Г.1. Распространение волны через границу раздела.
|
Г' ^і, і-і Е' ^ Я. і -1 |
|
Еи, |
|
= р |
|
При этом передаточная матрица Сдается вьфажением: |
|
|
 |
|
|
|
|
1 Рі-и |
|
Рі-и 1 |
|
1 |
|
Ї-и = |
|
|
|
А* = — и = Ь«Г |
|
Заметим, что с учетом (9.Г.4) и (9.Г.5) детерминант Р._х . = п./п._у Распространение волны в слое / учитывается с использованием константы распространения к. или: |
|
(9.Г.8) |
|
= А |
|
К, Е’к, Здесь А — дефазирующая матрица: А = |
|
Е'. |
|
Я/-! |
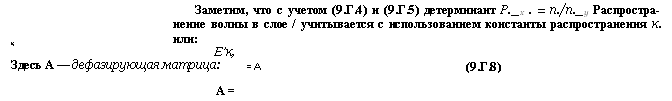 |
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
||
|
Г,„ =— и Т,„ = -^|г,„|2 (9.Г.12)
/1,
Отметим, что яш +ТШ = (|512р + лул^/Щ2 = 1, поскольку <1е1(3) = п„/пх. Это последнее равенство означает, что световой поток сохраняется, и это само по себе поддерживает нас в нашем рассмотрении!